[题解] [NOIP2011 提高组] Mayan 游戏

题目描述

有一个 \(7\) 行 \(5\) 列的格子棋盘，有的格子上有方块。方块有重力，即如果一个方块下面没有其他方块，他就会往下掉，直到触底或者下面有方块为止。

每个方块都有自己的颜色，如果连着三个竖着或者横着的方块颜色相同，它们就会消除。如果出现了共用方块的情况，则共用这一个方块的两组全部消除。

你可以进行 \(n\) 步操作，每一步操作如下：

选择一个方块，将它向左移动一格或者向右移动一格，如果移动的目标格子已经有方块了，就交换这两个方块。如果移动后有方块悬空，它们就会落下。

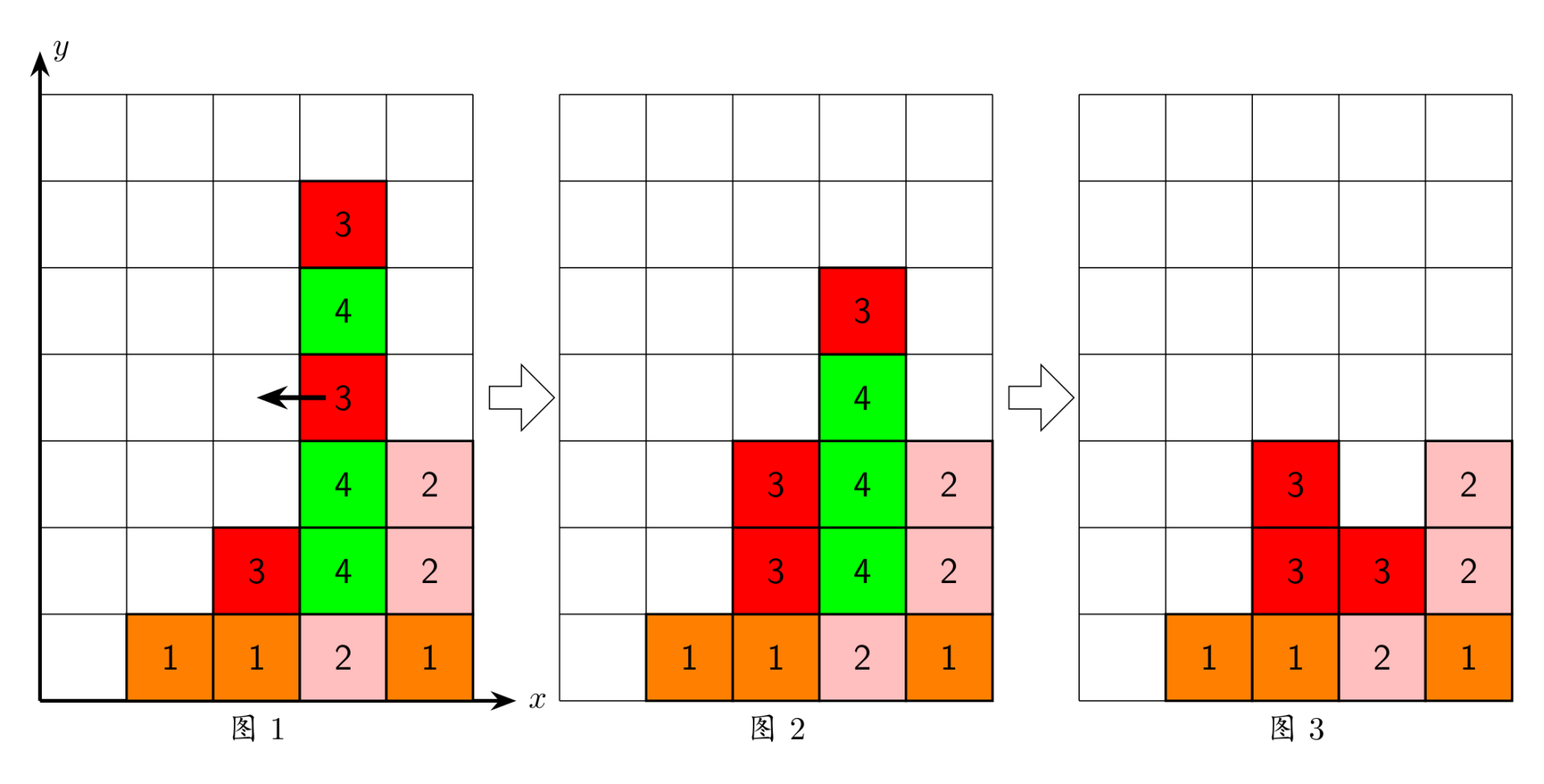
你的目标是消除所有的方块。

输入格式

共 \(6\) 行。

第一行为一个正整数 \(n(0 < n \leq 5)\) ，表示要求游戏通关的步数。

接下来的 \(5\) 行，描述 \(7 \times 5\) 的游戏画面。每行若干个正整数，以 \(0\) 结束。自下向上表示每竖列方块的颜色编号（颜色不多于 \(10\) 种，从 \(1\) 开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式

如果有解决方案，输出 \(n\) 行，每行包含 \(3\) 个整数 \(x,y,g\) ，表示一次移动，每两个整数之间用一个空格隔开，其中 \((x,y)\) 表示要移动的方块的坐标，\(g\) 表示移动的方向，\(1\) 表示向右移动，\(−1\) 表示向左移动。注意：多组解时，按照 \(x\) 为第一关键字，\(y\) 为第二关键字，\(1\) 优先于 \(−1\) ，给出一组字典序最小的解。游戏界面左下角的坐标为 \((0,0)\) 。

题解

很明显，这是一道搜索题，而且还是个大模拟。解决这个问题首先要仔细考虑好每一步可能发生的过程。

最直观的过程是我们的操作本身，也就是块的移动，实际上无论目标位置是否有块都可以视为块的交换，只不过没块的时候是和空气交换，移动过后可能会出现两种情况：有块可以消除、有块腾空。腾空的块可能是我们操作的那个方块，也有可能是原本落在我们操作的那个方块上面的方块。

考虑块腾空的过程，实际上就是不断的下落，用一个循环即可解决：如果没落到最下层或者下面有方块，就把这个方块往下移一位。

考虑块的消除，我们可以在每次操作之后都进行一次判断消除的更新操作。这个操作分为两步：判断哪些块需要消除、消除需要消除的块。为什么不合成一步做呢？因为那样就不能处理块被共用的情况 （踩过的坑） 。我们用一个简单循环就可以判断需要消除的块。删除一个块就把这个块上面的块都往下移一位即可。

过程考虑的差不多了，就要考虑状态的处理了。看这个数据规模，暴搜！由于题目有步骤要求的顺序，我们按照给定的顺序考虑枚举操作就可以在第一次全部消除时就得到答案。即从左下角开始每一列从下到上，再从左到右枚举操作的块即可，操作时先枚举向右的操作再枚举向左的操作。这么做无形就可以剪掉很多枝。

把上面的过程调试好之后，还没有考虑剪枝，试着交了一发，没想到A了... ...

后来仔细思索了一下，除非能直接判断当前的状态一定不能得到解，否则哪怕浪费步骤也要往下搜索，因为本题的答案是唯一的。所以大部分题解的剪枝都是没有必要的， 所以本题不需要剪枝 。

由于代码量大，采用了比较粗糙的模块化的面向对象写的。

AC 代码

#include <iostream>
using namespace std;

const int R = 1;
const int L = -1;
const int MAXN = 10;

// 存下操作以供输出
class Op {
public:
    int x, y, dir;
};

class State { // 封装的dfs的状态
public:
    int map[MAXN][MAXN]; // 该状态下的地图
    Op op[103]; // 到该状态所用的操作
    int cnt; // 操作数量
    void output() { // 输出答案操作
        for (int i = 1; i <= cnt; i++) {
            // 由于我使用的坐标是数组意义上的坐标，和题目中给出的几何意义的坐标不一致，需要转换一下
            int nx = op[i].y - 1;
            int ny = 7 - op[i].x;
            cout << nx << ' ' << ny << ' ' << op[i].dir << '\n';
        }
    }
    void move(int x, int y, int dir) { // 移动其中一个方块
        // 记录操作
        op[++cnt].x = x;
        op[cnt].y = y;
        op[cnt].dir = dir;
        // 交换方块
        int tmp = map[x][y + dir];
        map[x][y + dir] = map[x][y];
        map[x][y] = tmp;
        // 处理原来的位置上面的方块的下落
        if (tmp == 0) {
            del(x, y);
        }
        // 处理它自己的下落
        y = y + dir;
        for (int i = x + 1; i <= 7 && map[i][y] == 0; i++) {
            map[i][y] = map[i - 1][y];
            map[i - 1][y] = 0;
        }
        // 处理消除方块
        update();
    }
    void del(int x, int y) { // 删除其中的一个方块
        for (int i = x; i > 0; i--) {
            map[i][y] = map[i - 1][y];
        }
    }
    void update() { // 处理消除
        bool d[10][10]; // 记录每一次发现的需要删除的方块
        while (true) {
            for (int i = 1; i <= 7; i++)
                for (int j = 1; j <= 5; j++)
                    d[i][j] = false;
            bool flag = false; // 这一轮有没有消除过方块
            for (int i = 1; i <= 7; i++) { // 处理横向消除
                for (int j = 3; j <= 5; j++) {
                    if (!map[i][j]) continue; // 没有方块就跳过
                    if (map[i][j] == map[i][j - 1] && map[i][j] == map[i][j - 2]) { // 横着连着三个一样
                        // 把他们三个标记为消除
                        d[i][j] = true;
                        d[i][j - 1] = true;
                        d[i][j - 2] = true;
                        flag = true;
                    }
                }
            }
            for (int j = 1; j <= 5; j++) { // 处理纵向消除
                for (int i = 3; i <= 7; i++) {
                    if (!map[i][j]) continue; // 没有方块就跳过
                    if (map[i][j] == map[i - 1][j] && map[i][j] == map[i - 2][j]) { // 竖着三个一样
                        // 把他们三个标记为消除
                        d[i][j] = true;
                        d[i - 1][j] = true;
                        d[i - 2][j] = true;
                        flag = true;
                    }
                }
            }
            for (int i = 1; i <= 7; i++) {
                for (int j = 1; j <= 5; j++) {
                    // 删除标记为消除的方块，注意要从上往下删除，不然可能删成掉落下来的
                    if (d[i][j]) del(i, j);
                }
            }
            if (!flag) break; // 如果这一轮没有消除，说明更新好了，退出循环
        }
    }
    int tot() { // 获取没有被消除的方块总数
        int tmp = 0;
        for (int i = 1; i <= 7; i++) {
            for (int j = 1; j <= 5; j++) {
                if (map[i][j]) tmp++;
            }
        }
        return tmp;
    }
} start;

int k; // 题目中给出的步数

void dfs(State state) { // 深度优先搜索
    if (state.cnt == k) { // 如果刚好等于步数，看看是不是全消了
        if (state.tot() == 0) { // 找到了答案
            state.output();
            exit(0);
        }
        return;
    }
    for (int j = 1; j <= 5; j++) {
        for (int i = 7; i > 0; i--) { // 枚举要移动的方块
            if (state.map[i][j] == 0) continue; // 如果没有方块就跳过
            if (j != 5) { // 只要不在最右边，向右移动
                // 获取向右移动后的状态并继续搜索
                State stateR = state;
                stateR.move(i, j, R);
                dfs(stateR);
            }
            if (j != 1) { // 只要不在最左边，向左移动
                // 获取向左移动后的状态并继续搜索
                State stateL = state;
                stateL.move(i, j, L);
                dfs(stateL);
            }
        }
    }
}

int main() {
    cin >> k;
    // 输入原始状态
    for (int j = 1; j <= 5; j++) {
        int x;
        cin >> x;
        for (int i = 7; i > 0 && x; i--) {
            start.map[i][j] = x;
            cin >> x;
        }
    }
    // 深度优先搜索
    dfs(start);
    // 如果没找到，输出-1
    cout << -1 << '\n';
    return 0;
}