本文可能含有:部分代码省略,部分资源来源于网络,极其模糊不清的语言表述,粗浅到浮于言表的对于此算法的认识。
本文仅用于个人学习与报告使用。若有侵权,请洛谷私信联系笔者要求删除。
就连上述文字都是抄袭大佬 @GClock_519 的,可以看得出笔者拙劣的语文水平(
图的连通性相关,顾名思义,可以理解为与「图是否连通」相关的性质。
具体来说,可以分为无向图的双连通性与有向图的强连通性。
有向图的强连通性
先说一下定义。一个有向图 \(G\) 强连通指的是 \(G\) 中所有点互相(直接或间接地)可达。
我们不讨论无向图是否强连通,因为显然一个无向连通图任意两个点都互相可达。
引入强连通分量(简称 SCC)的概念:极大的强连通子图。「子图」很好理解,可「极大」是什么意思呢?我们可以感性理解为尽可能大。具体地,指该强连通图不是任何一个强连通图的子图。
例如有一个图:
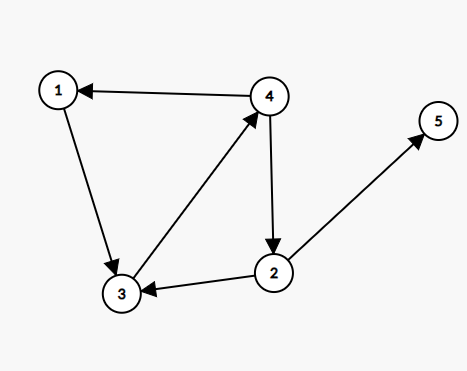
我们发现 \(1,3,4\) 三个点互相可达,可以构成一个强连通子图(记作 \(\{1,3,4\}\))。但是 \(\{1,3,4\}\) 确实另一个更大的强连通图 \(\{1,3,4,2\}\) 的子图。所以我们说 \(\{1,3,4,2\}\) 是一个强连通分量,而 \(\{1,3,4\}\) 不是一个强连通分量。
所以怎么求强连通分量呢?
Tarjan 算法
你说得对,但是 Robert E. Tarjan(罗伯特·塔扬,1948~),生于美国加州波莫纳,计算机科学家。Tarjan 发明了很多算法和数据结构。不少他发明的算法都以他的名字命名,以至于有时会让人混淆几种不同的算法。比如求各种连通分量的 Tarjan 算法,求 LCA(Lowest Common Ancestor,最近公共祖先)的 Tarjan 算法。并查集、Splay、Toptree 也是 Tarjan 发明的。
Tarjan 爷爷 Orz。
直接来看 Tarjan 算法的操作流程。我们考虑从任意一个结点开始 dfs,并记录每个点被搜到的时间(也称为「时间戳」),记为 \(dfn_i\)。
同时,想象有一个栈,当结点刚被遍历到,即当前不属于任何一个强连通分量时塞入栈中。定义每个结点可以访问到的、时间戳最小的、在栈内的点的时间戳为 \(low_i\)。
考虑怎么求 \(dfn_i\)。显然 dfs 一遍,在每个点第一次被遍历到的时候更新当前结点时间戳即可。
可以发现,我们遍历过的边会成为原图的一棵子树。遂把这些边成为树边。那么这个图显然还有一些非树边,我们这么定义:
- 指向祖先结点的边,称为返祖边;
- 指向孙子结点的边,称为前向边;
- 由时间戳大的点 \(u\) 指向时间戳小的且非 \(u\) 的祖先的点 \(v\) 的边,称为横叉边。
可能有点抽象,可以参考 OI Wiki 的具体例子理解。
接下来考虑怎么求 \(low_i\)。首先我们有:
- 当这个结点刚被遍历到的时候,\(low_i = dfn_i\)。
然后对于一个点 \(u\),如果 \(low_u\) 可更新,有如下几种情况:
- 我们通过「返祖边」,访问到了 \(dfn\) 更小的点 \(v\),\(low_u \gets dfn_v\)。【处理返祖边】
- 子结点 \(v\) 的 \(low\) 已经被更新得更小,\(low_u \gets low_v\)。
于是我们可以发现:对于栈内每一个 \(low\) 相等的点,他们是在同一个强连通分量里面的。【只考虑「栈内」是防止横叉边使得 \(low\) 被乱更新,即处理横叉边】
我们找到栈中一个 \(dfn_u = low_u\) 的点、也是当前强连通分量中第一个入栈的点,让其称为该强连通分量的「根」,并把栈中在它之上的点统统统计并出栈。这些点共同构成一个强连通分量。
为什么是 \(dfn_u = low_u\) 呢?我们发现,当 \(low_u = dfn_u\) 时,说明沿着 \(u\) 向下更新可以到达自身。那么它就是该强连通分量中时间戳最小的点(也就是最先入栈的点)、以及 SCC 的若干点在 dfs 生成树中的祖先。
发现并没有前向边什么戏份,的确前向边也不会影响(
总结一下 Tarjan 算法流程:
- 选个没被访问的点 \(u\),入栈,初始化 \(dfn\) 以及 \(low = dfn\),进行 dfs。
- 如果连着的点 \(v\) 也没被访问,先递归更新 \(v\),然后 \(low_u \gets \min(low_u, low_v)\)。
- 如果是通过「返祖边」遍历到已在栈中的点 \(v\),则 \(low_u \gets \min(low_u, dfn_v)\)。
- 遍历所有点后,若 \(dfn_u = low_u\),将同一强连通分量的点统统出栈并统计,直到 \(u\) 被弹出。
- 找没被访问过的点,重复步骤 \(1\)。
Code:
int dfn[N], low[N], vis[N], col[N]; // low 表示每个点可以遍历到的最小的时间戳,dfn 表示每个点的时间戳。
// vis 表示每个点在不在栈里面。
// col 表示每个点所在的强连通分量的编号。
vector<int> st; // 栈。
int dfncnt, colcnt;
void tarjan(int u)
{
if(!dfn[u]) dfn[u] = low[u] = ++dfncnt;
vis[u] = 1;
st.push_back(u); // 放入栈。
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i];
if(!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]); // 如果 v 没遍历过就求 v 然后更新。
else if (vis[v]) low[u] = min(low[u], low[v]); // 如果 v 遍历过了而且在栈中就直接更新。
// 否则 v 已经在某个强连通分量里面了,不用管。
}
if(dfn[u] == low[u]) { //u 是某个强连通分量的跟。
colcnt++;
while(st.back() != u) {
int v = st.back();
col[v] = colcnt;
vis[v] = 0;
st.pop_back();
}
col[u] = colcnt;
vis[u] = 0;
st.pop_back();
}
}
上面是我用语言描述的算法流程,可能抽象得只有我一个人能看懂。
推荐观看 此视频 以更加深刻理解 tarjan 求 SCC。
应用:缩点
可以发现:如果把一个强连通分量替换成一个点,不挪动与外界的入边和出边,可以形成一个有向无环图。「有向」是因为原图为有向图,「无环」是因为一个环显然属于某个强连通分量,会被缩掉。
然后就可以在这个 DAG 图上面乱搞进行一些操作了,例如记搜、拓扑排序、最短路 等。
看这题:【模板】缩点。我们需要找到经过点权之和最大的路径。想象一下,我们如果在一个强连通分量里面走,那么我们得把每个点都踩一遍(因为点权 \(\ge 0\))。因此我们把缩成的点点权赋为该强连通分量所有点点权之和,再在新图上跑拓扑即可。
不过「把每个点都踩一遍」有一个限制:允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。这句话很重要,看到这句话要优先想到 Tarjan 缩点这个模型。
不知道说啥了,贴个模板题代码吧:
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
const int N = 10010, M = 100010;
int n, m;
int V[N];
int nxt[M], to[M], fr[M], hd[N], idx;
void add(int u, int v) {
nxt[++idx] = hd[u], fr[idx] = u, to[idx] = v, hd[u] = idx;
}
int dfn[N], low[N], vis[N], dfnCnt;
vector<int> st;
int colCnt, col[N], colV[N];
void tarjan(int u) {
if(!dfn[u]) dfn[u] = low[u] = ++dfnCnt;
vis[u] = 1; st.push_back(u);
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i];
if(!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
else if (vis[v]) low[u] = min(low[u], low[v]);
}
if(dfn[u] == low[u]) {
colCnt++;
while(st.back() != u){
int x = st.back();
col[x] = colCnt;
colV[colCnt] += V[x];
vis[x] = 0;
st.pop_back();
}
col[u] = colCnt; vis[u] = 0; st.pop_back(); colV[colCnt] += V[u];
}
}
int in[N], dis[N];
int topo() {
queue<int> q;
for (int i = 1; i <= n; i++) {
if(!in[i]) dis[i] = colV[i], q.push(i);
}
int ans = 0;
while(q.size()) {
int u = q.front(); q.pop();
ans = max(ans, dis[u]);
for (int i = hd[u]; i; i = nxt[i]) {
int v = to[i]; in[v]--;
if(!in[v]) q.push(v);
dis[v] = max(dis[v], dis[u] + colV[v]);
}
}
return ans;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &V[i]);
for (int i = 1; i <= m; i++) {
int u, v; scanf("%d%d", &u, &v);
add(u, v);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; i++) hd[i] = 0;
idx = 0;
for (int i = 1; i <= m; i++) {
int u = fr[i], v = to[i];
if(col[u] == col[v]) continue;
add(col[u], col[v]); in[col[v]]++;
}
n = colCnt, m = idx;
printf("%d", topo());
return 0;
}
一个比较好的 SCC & 缩点基础题题单:强连通分量 & 缩点。
例题
1. P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G
题意:一个有向图,输出所有点直接或直接或间接可达的点(称为「明星点」)的数量。
经典题。我们发现一个强连通分量的点互相连通,考虑缩点得到拓扑图,利用拓扑图性质简化思考。
接下来,对于每个点,如果他是明星点,那么显然它不能有出边(出边指向的点不能到达它自身,因为 DAG 无环)。也就是说,它得出度为 \(0\)。
所以输出出度为 \(0\) 的强连通分量结点数即可?
你先别急。假如新图有两个出度为 \(0\) 的点,则这两个点互相不可达!此时「明星点」数量为 \(0\)。
统计每个强连通分量的入度、所含点数即可。代码很好写就不放了。
2. P7251 [JSOI2014] 强连通图
题意很清晰就不放了。
第一问很好想,无向图上若干个点互相可达,就差把求强连通分量印在题面了。对于所有强连通分量点数取 \(\max\) 即可。
考虑第二问。同样很经典。我们发现:把一个入度为 \(0\) 的点 \(u\) 和出度为 \(0\) 的点 \(v\) 相连,可以得到一条环。我们就可以缩成一个点了。
于是我们将所有入度为 \(0\) 的点和出度为 \(0\) 的点两两相连(多余的出度(入度)为 \(0\) 的点同样找原入度(出度)为 \(0\) 的点连接),这样可以把整个图缩成一个点。那么答案为 \(\max(\text{入度为 0 的点个数}, \text{出度为 0 的点个数})\)。
3. P2169 正则表达式
看到题目先想到最短路。但是题目有一个限制:如果两点 \(u, v\) 互相可达,那么从 \(u\) 到 \(v\) 无论走多少条边都不需要花费边权。
互相可达,显然就是求强连通分量嘛。所以缩点后再跑最短路即可。
无向图的边双连通性
如果一个无向图 \(G\) 删去任意一条边后,原图仍连通,那么我们把 \(G\) 称为边双连通图。
当然总有一些图(记作 \(G'\))删去某条边后图不连通了。我们把删去后 \(G'\) 不连通的那若干条边叫做割边。
换句话说,没有割边的无向图就是边双连通图。
如下图为一个边双连通图。
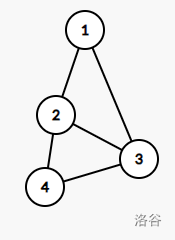
我们删去任意一条边,原图仍连通。
而下图不是一个边双连通图:
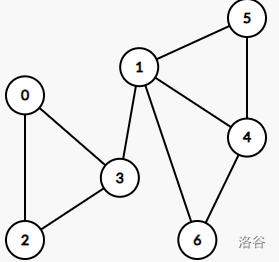
我们删去边 \(3\to 1\) 后原图就不连通了。\(3 \to 1\) 就是原图的割边。
类比强连通分量的定义,极大的边双连通子图就是边双连通分量。一个无向图的边双连通分量不是任何该图的边双连通子图的子图。
特别地,一个点可能是一个边双连通分量。一个孤点必然为一个边双连通分量。
我们同样使用 Tarjan 算法求割边。
Tarjan 算法
我们同样选择一个点 dfs 整一个生成树。类比 Tarjan 求 SCC,定义 \(dfn_i\) 为时间戳,\(low_i\) 为结点 \(i\) 只通过一条非树边(和若干条树边)能访问到的最小的时间戳。\(dfn\) 和 \(low\) 是 Tarjan 的核心。
我们发现,此时不需要定义一个栈来避免已被更新过的边双被横叉边干扰。因为无向图 dfs 生成树中不存在横叉边。简略证明:
假设无向图的 dfs 树中存在边 \(u \to v\)(其中 \(u\) 不为 \(v\) 的祖先),那么当我们 dfs 搜到结点 \(u\) 时也可以直接搜到 \(v\),让 \(u \to v\) 成为树边。故不存在横叉边,命题得证。
先来看怎么求割边吧。
求割边
\(dfn\) 初值求法是和强连通分量的 Tarjan 一样的,直接求 dfs 序就可以了。不再赘述。注意别访问 \(\text{子} \to \text{父}\) 边。
然后考虑求 \(low\)。对于一条边 \(u \to v\),若 \(v\) 已经访问过(即 \(dfn_v \ne 0\))那么这条边为返祖边或前向边。前向边的 \(dfn_v\) 是大于 \(dfn_u\) 的,不用管。如果 \(dfn_v \le low_u\),则 \(u \to v\) 为返祖边,根据定义更新 \(low_u \gets dfn_v\)。
若 \(v\) 没被访问,则 \(u \to v\) 为树边,先搜下去,求出 \(v\) 的 \(low\) 值再更新 \(low_u = \min(low_u, low_v)\) 即可。
那么怎么判断割边呢?对于一条边 \(u \to v\),分以下几种情况:
- \(low_v < dfn_u\),则通过 \(v\) 只走一条返祖边可以访问到 \(u\) 的祖先。也就是说 \(u\) 的祖先有两种走法可以到 \(v\)。那它们是在一个边双里面的,显然 \(u \to v\) 不为割边。
- \(low_v = dfn_u\),同理,\(u\) 和 \(v\) 在一个边双里面,当前边不是割边。
- \(low_v > dfn_u\),说明 \(v\) 无法访问到时间戳 \(\le dfn_u\) 的边。如果我们将 \(u \to v\) 切断,\(v\) 就无法与 \(u\) 连通了。说明 \(u \to v\) 为割边。
综上即为割边算法。代码与边双写一起了。
求边双
我们同样使用一个栈存结点,当结点刚被搜到时入栈。同样定义一个边双连通分量 \(dfn\) 最小的结点为它的根。
类似地,我们发现这个边双连通分量的所有结点的 \(low\) 值都为根的 \(dfn\) 值。同理,判断结点 \(u\) 是否为根即判断 \([dfn_u = low_u]\) 即可。
找到根后,我们弹栈,知道弹出 \(u\)。弹出的这些结点就在一个边双里面了。
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int N = 500010, M = 4000010;
int n, m;
struct Graph {
int nxt[M], to[M], hd[N], idx;
bool cut[M];
Graph() {
idx = 1; for (int i = 1; i < N; i++) hd[i] = 0;
for (int i = 1; i < M; i++) cut[i] = 0;
};
void add(int u, int v) {
nxt[++idx] = hd[u], to[idx] = v, hd[u] = idx;
}
} G;
int low[N], dfn[N], dc;
int id[N], idc;
vector<int> st;
vector<int> ans[N];
void tarjan(int u, int faE) {
dfn[u] = low[u] = ++dc;
st.push_back(u);
for (int i = G.hd[u]; i; i = G.nxt[i]) {
if(i == (faE ^ 1)) continue; //注意不要访问 子->父 边,但因为可能有重边所以得这么写
int v = G.to[i];
if(!dfn[v]) {
tarjan(v, i);
if(low[v] > dfn[u]) G.cut[i] = 1; // 是割边
low[u] = min(low[u], low[v]);
}
else low[u] = min(low[u], dfn[v]);
}
if(low[u] == dfn[u]) { // 弹栈统计
idc++;
while(st.back() != u) {
int v = st.back();
st.pop_back();
id[v] = idc;
ans[idc].push_back(v);
}
st.pop_back();
id[u] = idc;
ans[idc].push_back(u);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int u, v;
scanf("%d%d", &u, &v);
G.add(u, v);
G.add(v, u);
}
for (int i = 1; i <= n; i++) if(!dfn[i]) tarjan(i, 0);
printf("%d\n", idc);
for (int i = 1; i <= idc; i++) {
printf("%d ", ans[i].size());
for (auto x : ans[i]) printf("%d ", x);
printf("\n");
}
return 0;
}
无向图的点双连通性
与边双连通性定义很像。我直接复制粘贴上面并加粗的不一样的地方了。
如果一个无向图 \(G\) 删去任意一个点(和其所连边)后,原图仍连通,那么我们把 \(G\) 称为点双连通图。
当然总有一些图(记作 \(G'\))删去某个点后图不连通了。我们把删去后 \(G'\) 不连通的那若干个点叫做割点。
极大的点双连通子图就是点双连通分量。一个无向图的点双连通分量不是任何该图的点双连通子图的子图。
特别的,两个点用一条边相连组成的图可能为一个点双连通分量。点双有两种表现形式:
- 孤点。
- 两个点用一条边相连组成。
- \(\ge 2\) 个点。其中每两个点都在点双的一个简单环(就是我们平时认为的环)上。
同样,我们观察点双连通分量与割点的关系。不难发现两个点双可以相交,有且仅有一个交点,为割点。
两个点双相交的例子如下:

如上图相同颜色的所有结点组成一个点双。
简单证明:
假设原连通图 \(G\) 中的两个点双连通分量 \(G_1, G_2\)。若 \(G_1\) 和 \(G_2\) 有多个交点,那么我们删去其中任意一个交点,\(G_1\)、\(G_2\) 仍联通,与点双的定义矛盾。命题得证。
我们同样使用 Tarjan 算法。
Tarjan 算法
定义和边双完全一样,此处略。
不过求割点和求点双不尽相同。
求割点
求 \(dfn\) 和求 \(low\) 和边双完全一样,我踏马略略略略略。重点讲怎么求割点。
-
对于一个 非 dfs 树根结点 \(u\),我们寻找 dfs 生成树上的 \(u\) 的子孙 \(v\)。如果 \(low_v \ge dfn_u\),说明 \(v\) 没法只通过一条返祖边访问到 \(u\) 以上的结点。那么我们此时把 \(u\) 断掉,\(v\) 就上不去了!
所以当存在 \(low_v \ge dfn_u\) 时,\(u\) 为割点。
需要注意的是当 \(u\) 为树根结点时,\(low_v\) 是一定小于 \(dfn_u\) 的。而根结点不一定为割点。所以我们上述结论对根结点不适用。
-
当根结点连着多条树边时,我们断掉根结点,剩下的子树就不连通了。所以当根结点所连树边数量 \(\ge 2\) 时其为割点。
模板题(P3388 【模板】割点)代码如下:
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int N = 100010;
int n, m;
vector<int> G[N];
int dfn[N], low[N], dc;
bool f[N];
void tarjan(int u, int fa, int ro) {
dfn[u] = low[u] = ++dc;
int ch = 0; // 儿子数量
for (int v : G[u]) {
if(v == fa) continue; // 不考虑子 -> 父
if(!dfn[v]) { // 没被遍历过,是儿子
ch++;
tarjan(v, u, ro);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u] && u != ro) f[u] = 1; // 记得判断 u 是否为根结点
}
else low[u] = min(low[u], dfn[v]);
}
if(ch >= 2 && u == ro) f[u] = 1; // 特判跟结点
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int u, v;
scanf("%d%d", &u, &v);
G[u].push_back(v), G[v].push_back(u);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i, -1, i);
int ans1 = 0;
for (int i = 1; i <= n; i++) if (f[i]) ans1++;
printf("%d\n", ans1);
for (int i = 1; i <= n; i++) if(f[i]) printf("%d ", i);
return 0;
}
求点双
咕咕咕~(并没有完全理解.jpg)
标签:tarjan,连通性,int,结点,连通,笔记,dfn,low,分量 From: https://www.cnblogs.com/Running-a-way/p/18150525