基环树那块闲了再写。
本文针对虚树板题作原理解释和介绍写法。
如果不考虑多测那么这是一道裸的树形dp。
令 \(dp_u\) 表示切断以 \(u\) 为根的子树里所有关键点的最小花费。
\[ans=dp_{root}=dp_1 \]\[dp_u=min(minv_u,\sum_{v\in son_u}dp_v) \]其中 \(minv_u\) 表示切断路径 \(1->u\) 的最小花费。可以容易地实现 \(O(n)\) 预处理
也就是:要么把 \(u\) 切了,要么把 \(u\) 的儿子中的路都切了。
时间复杂度 \(O(n)\),加了多测是 \(O(nm)\)。会导致TLE。
考虑优化,注意到 \(\sum k\) 与 \(n\) 同阶,也就是在 \(m\) 足够大时,树中的大部分节点是无用的,我们不需要管没有关键点的节点,而且 \(root\) 到关键点的路径上也有大多数点是无用的,因为 \(minv_i\) 已经帮我们实现了断开位置的选取。
也就是说,唯一有用的点是查询的关键点和他们的 \(lca\)。
用这些点捏一棵新的树,则 \(m\) 颗新树的大小之和与 \(n\) 同阶,新树上的转移方程是适用的。
这里借用题解的图方便理解。
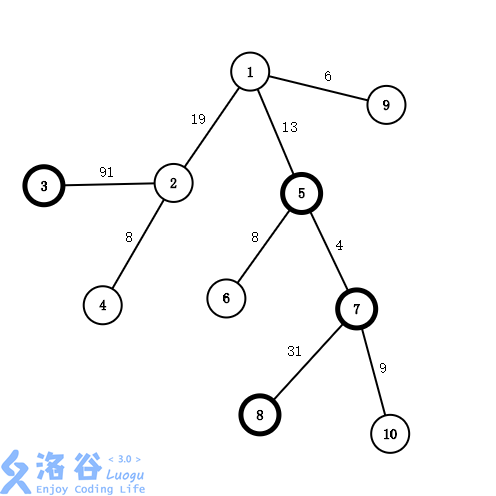
从原树中提取的新树长这样。
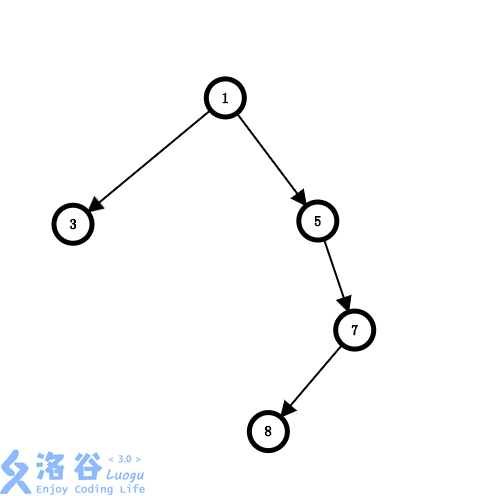
可以发现,答案没有变化。
这个思想就叫做虚树。
现在考虑如何构建虚树。
构建思想和笛卡尔树很像,都使用单调栈维护右链的方式。
首先把关键点按 dfs序 排序,将第一个点入栈。
令 \(lca\) 表示待添加节点 \(u\) 与 \(stac_{top}\) 的最近公共祖先。然后讨论如何加入。
- \(lca=stac_{top}\)
说明节点 \(u\) 就在栈顶节点的子树中,直接加入右链。
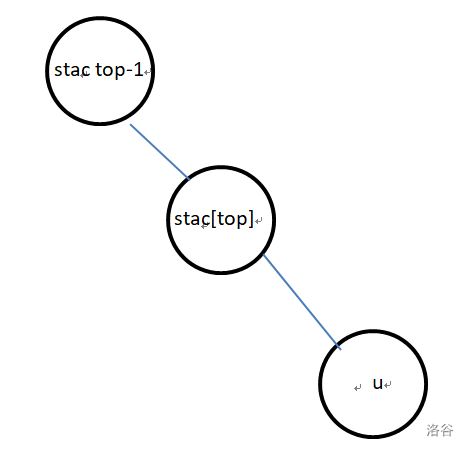
- lca 在 \(stac_{top}\) 到 \(stac_{top-1}\) 的路径上。
此时弹出 \(stac_{top}\),把 \(lca\) 和 \(u\) 压入栈中。
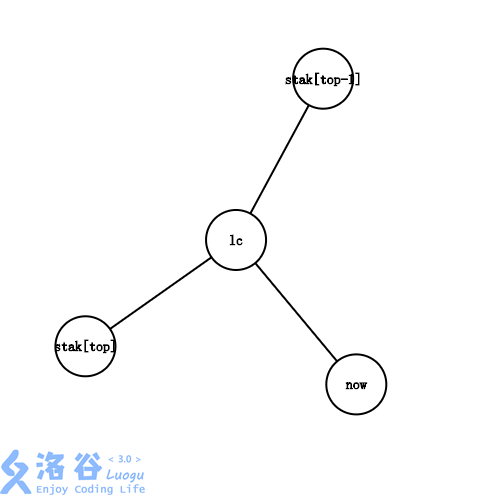
- \(lca=stac_{top-1}\)
这个时候只弹栈顶,把 \(u\) 入栈。
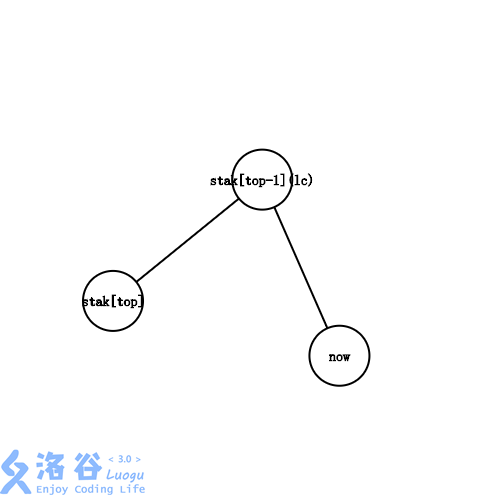
- \(dep_{lca}<dep_{stac_{top-1}}\)
此时 \(stac_{top}\) 和 \(stac_{top-1}\) 没法界定 \(stac\) 了,那就一直弹栈顶连边直到满足上面三种情况之一,然后把 \(lca\) 和 \(u\) 入栈。
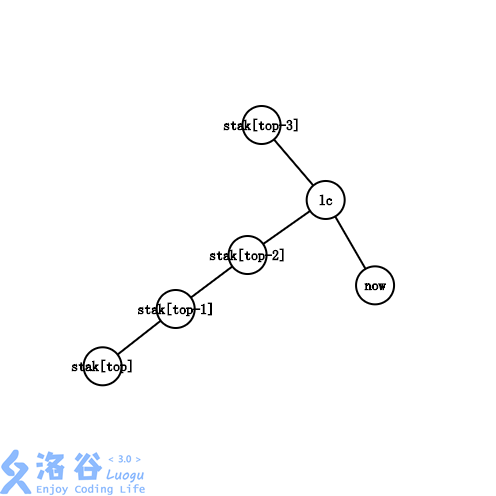
于是可以跑出本题的虚树的建树过程。
for(int i=2;i<=k;i++){
int u=tar[i],anc=lca(u,stac[tt]);//跑出lca
while(1){
if(dep[anc]>=dep[stac[tt-1]]){//第四种情况以外的情况,此时stactop和stactop-1能够界定lca的位置。
if(anc!=stac[tt]){//只要lca不是栈顶那就得踢掉(2,3种情况)
readd(anc,stac[tt]);
if(anc!=stac[tt-1])stac[tt]=anc;//第二种情况。
else --tt;//第三种情况。
}
break;
}
else{
readd(stac[tt-1],stac[tt]);
--tt;
}
}
stac[++tt]=u;//无论如何 u 都入栈。
}
最后右链很可能还是有东西的,把右链逐个连边。
while(--tt)readd(stac[tt],stac[tt+1]);
然后在新图上跑 \(dp\) 就可以了,不过要注意跑的时候还要顺带把图给拆了,这时向量的拆图效率就不如前向星。
提供完整代码。
#include<bits/stdc++.h>
#define MAXN 500005
#define int long long
using namespace std;
int n,m,k;
const int inf=1e18;
struct node{
int v,w,nxt;
}edge[MAXN];
int h[MAXN],tmp;
inline void add(int u,int v,int w){
edge[++tmp].v=v;edge[tmp].w=w;
edge[tmp].nxt=h[u];
h[u]=tmp;
}
int lcafa[25][MAXN],dfn[MAXN],tim,dep[MAXN],minv[MAXN];
inline void dfs1(int u){
for(int i=0;lcafa[i][u];i++){
lcafa[i+1][u]=lcafa[i][lcafa[i][u]];
}
dfn[u]=++tim;
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v,w=edge[i].w;
if(!dfn[v]){
dep[v]=dep[u]+1;
minv[v]=min(minv[u],w);
lcafa[0][v]=u;
dfs1(v);
}
}
}
inline int lca(int x,int y){
if(dep[x]<dep[y])swap(x,y);
for(int i=20;i>=0;i--){
if(dep[lcafa[i][x]]>=dep[y])x=lcafa[i][x];
}
if(x==y)return x;
for(int i=20;i>=0;i--){
if(lcafa[i][x]!=lcafa[i][y]){
x=lcafa[i][x];
y=lcafa[i][y];
}
}
return lcafa[0][x];
}
inline void INIT(){
scanf("%lld",&n);
for(int i=1,u,v,w;i<n;i++){
scanf("%lld%lld%lld",&u,&v,&w);
add(u,v,w);
add(v,u,w);
}
minv[1]=inf;
dfs1(1);
}
bool cmp(int x,int y){
return dfn[x]<dfn[y];
}
int tar[MAXN];
bool que[MAXN];
int stac[MAXN],tt;
node nedge[MAXN];
int nh[MAXN],ntmp;
inline void readd(int u,int v){
nedge[++ntmp].v=v;
nedge[ntmp].nxt=nh[u];
nh[u]=ntmp;
}
inline int dfs(int u){
int sum=0,res=inf;
for(int i=nh[u];i;i=nedge[i].nxt){
int v=nedge[i].v;
sum+=dfs(v);
}
if(que[u])res=minv[u];
else res=min(minv[u],sum);
que[u]=0;
nh[u]=0;
return res;
}
inline void Work(){
scanf("%lld",&m);
while(m--){
scanf("%lld",&k);
for(int i=1;i<=k;i++)scanf("%lld",&tar[i]),que[tar[i]]=1;
sort(tar+1,tar+1+k,cmp);
tt=1,stac[tt]=tar[1];
for(int i=2;i<=k;i++){
int u=tar[i],anc=lca(u,stac[tt]);
while(1){
if(dep[anc]>=dep[stac[tt-1]]){
if(anc!=stac[tt]){
readd(anc,stac[tt]);
if(anc!=stac[tt-1])stac[tt]=anc;
else --tt;
}
break;
}
else{
readd(stac[tt-1],stac[tt]);
--tt;
}
}
stac[++tt]=u;
}
while(--tt)readd(stac[tt],stac[tt+1]);
printf("%lld\n",dfs(stac[1]));
ntmp=0;
}
}
signed main(){
INIT();
Work();
return 0;
}
虚树的 \(dfn\) 似乎与重链剖分的 \(dfn\) 不共用,第一遍用树剖打就打炸了,也可能是我自己的原因。
标签:int,tt,虚树,dep,stac,lca,lcafa From: https://www.cnblogs.com/Claimo0611/p/18134414