首页 > 其他分享 >虚树学习笔记

虚树学习笔记

时间：2024-01-27 22:34:12浏览次数：33  
标签：int Tr 笔记 学习 edge maxn tot dfn 虚树

虚树学习笔记

虚树，顾名思义，不是真实的树。

在关于树的问题中，虚树起到缩小题目规模，优化算法的作用。

算法思路

引入

P2495 SDOI2011 消耗战

设 \(dp[i]\) 为 \(i\) 与所有该子树内资源丰富节点不联通的代价。

如果 \(u\) 的儿子 \(v\)，不是资源丰富节点。

\[dp[u]+=\min(w(u,v),dp[v]) \]

如果 \(u\) 的儿子 \(v\)，是资源丰富节点。

\[dp[u]+=w(u,v) \]

每次询问都去跑一次这样的 \(dp\) 肯定会炸，但实际上每次 \(dp\) 值的转移只和这某些点有关，我们称这些点为关键点。

关键点

其实很多点是没有用的，如下图：

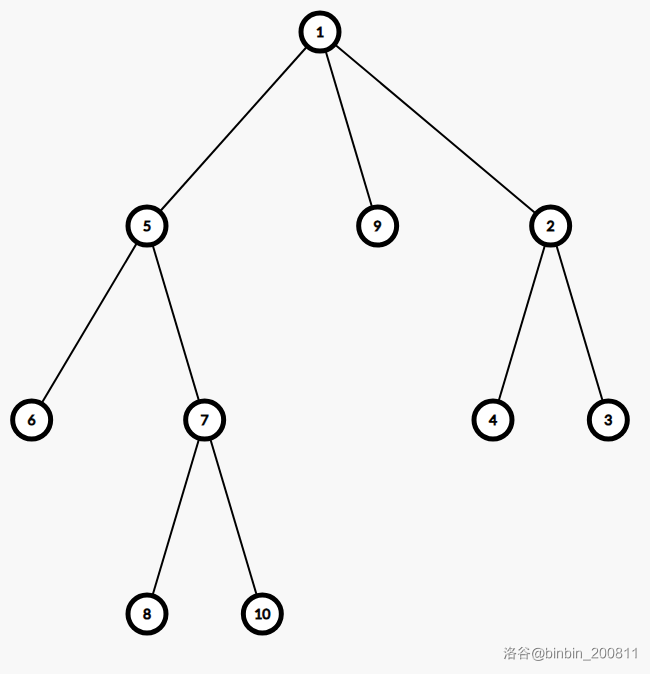
如果选择的关键点是：

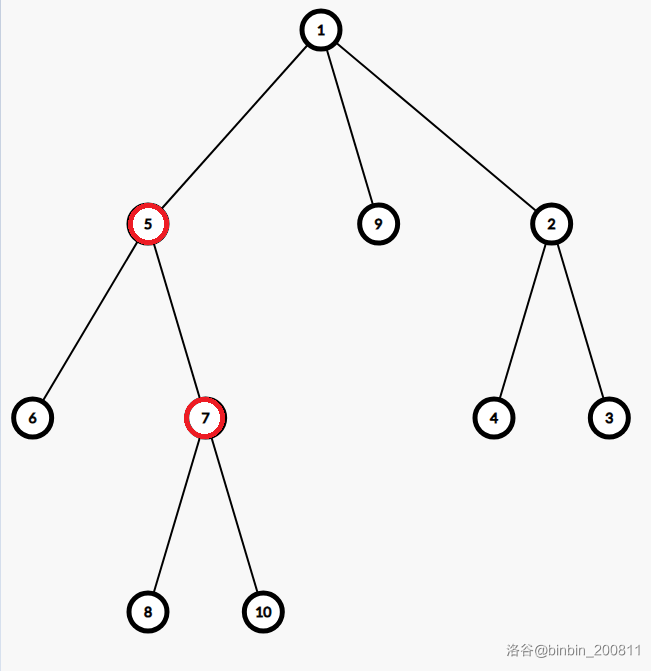
那么我们只需要保证 \(5\) 和 \(7\) 号点到达不到点 \(1\) 即可，无需遍历点 \(1\) 的其他子树。

我们的红色的点的个数级别是 \(O(n)\)，所以我们让红色点决定我们的复杂度是更优的。

总的来说，浓缩信息，大树变小树。

虚树

于是有了虚树这个概念。

我们先直观的看一些虚树的样子：

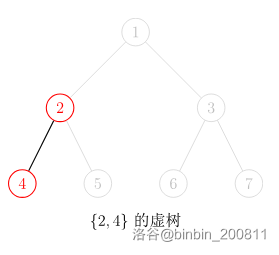
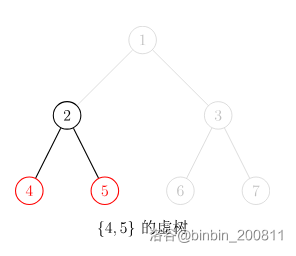
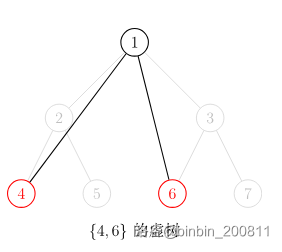
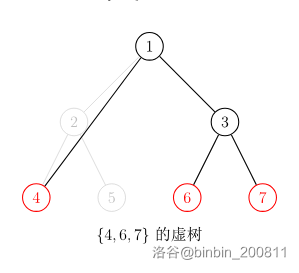
由于任意两个节点的 \(LCA\) 也是要保存和传递重要信息的，需要在虚树中留下他们。

而且虚树中的祖先关系并不会改变，也就是不会出现后代变前辈的伦理问题。

其实不难发现，虚树中只要节点数量足够，且先祖关系不变，那么我们无论添加多少个节点都不影响答案。

当然我们不可能两两枚举关键点去求 \(LCA\)​，于是我们引入 dfn 序解决问题。

为了方便，我们每次会将根加入虚树中。

构造思路

多个节点 \(LCA\) 可能不是同一个，所以我们不能多次将其加入虚树。

我们先看构造方法：

  • 将所有关键点按 dfn 升序排序
  • 遍历关键点相邻节点求 \(LCA\)，并判重。
  • 根据原树中的先祖关系建树。

问什么这样子建树可以不重不漏呢？

dfn 序相邻的两个节点中间肯定不会存在其他关键点，那么他们两个点的 \(LCA\) 肯定存在树上。

Q：有没有可能某两组节点的 \(LCA\)，又有新的 \(LCA\) 要加入虚树？

A：根据 dfn 构造，两个 \(LCA\)​ 子树中肯定存在 dfn 排序后相邻节点，故已经在虚树中。

时间复杂度 \(O(m\log n)\)，\(m\) 为关键点数， \(n\) 为原树点数，带一点点的小常数。

构建code
sort(a+1,a+k+1,cmp);
int len=0,rlen;
for(int i=1;i<k;i++)
{
    int lc;
    b[++len]=a[i];
    b[++len]=lc;
}
b[++len]=a[k];
b[++len]=1;
rlen=len;
sort(b+1,b+len+1,cmp);
for(int i=1;i<len;i++)
{
    if(b[i]==b[i+1]){rlen--;continue;}
    int lc=lca(b[i],b[i+1]);
    Tr.add(lc,b[i+1],dis(lc,b[i+1]));
    Tr.add(b[i+1],lc,dis(lc,b[i+1]));
}

回到引入

对关键点建虚树，跑 \(dp\) 就 OK 了。

CODE

#include<bits/stdc++.h>
using namespace std;

const int maxn=3e5+5;

struct Edge
{
    int tot;
    int head[maxn];
    struct edgenode{int to,nxt,val;}edge[maxn*2];
    inline void add(int u,int v,int z)
    {
        tot++;
        edge[tot].to=v;
        edge[tot].nxt=head[u];
        edge[tot].val=z;
        head[u]=tot;
    }
}G,Tr;

int n,m,dfncok;
int f[maxn][25],d[maxn][25],deep[maxn],a[maxn],b[maxn],dfn[maxn];

bool vis[maxn];

bool cmp(int x,int y){return dfn[x]<dfn[y];}

inline void dfs(int u)
{
    dfn[u]=++dfncok;
    for(int i=G.head[u];i;i=G.edge[i].nxt)
    {
        int v=G.edge[i].to;
        if(v==f[u][0]) continue;
        deep[v]=deep[u]+1;
        f[v][0]=u;
        d[v][0]=G.edge[i].val;
        for(int j=1;j<=20;j++) f[v][j]=f[f[v][j-1]][j-1],d[v][j]=min(d[v][j-1],d[f[v][j-1]][j-1]);
        dfs(v);
    }
}
inline int lca(int x,int y)
{
    if(deep[x]<deep[y]) swap(x,y);
    for(int i=20;i>=0;i--) if(deep[f[x][i]]>=deep[y]) x=f[x][i];
    if(x==y) return x;
    for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    return f[x][0];
}
inline int dis(int x,int y)
{
    int sum=1e6;
    if(deep[x]<deep[y]) swap(x,y);
    for(int i=20;i>=0;i--) if(deep[f[x][i]]>=deep[y]) sum=min(sum,d[x][i]),x=f[x][i];
    return sum;
}

bool cis[maxn];
long long dp[maxn];
inline void dfsdp(int u,int f)
{
    for(int i=Tr.head[u];i;i=Tr.edge[i].nxt)
    {
        int v=Tr.edge[i].to;
        if(v==f) continue;
        dfsdp(v,u);
    }
    for(int i=Tr.head[u];i;i=Tr.edge[i].nxt)
    {
        int v=Tr.edge[i].to;
        if(v==f) continue;
        if(cis[v]) dp[u]+=Tr.edge[i].val;
        else dp[u]+=min(dp[v],1ll*Tr.edge[i].val);
    }
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        G.add(x,y,z);
        G.add(y,x,z);
    }
    memset(d,0x5f,sizeof(d));
    deep[1]=1;
    dfs(1);
    scanf("%d",&m);
    while(m--)
    {
        int k;
        scanf("%d",&k);
        for(int i=1;i<=k;i++) scanf("%d",&a[i]),cis[a[i]]=1;
        sort(a+1,a+k+1,cmp);
        int len=0,rlen;
        for(int i=1;i<k;i++)
        {
            int lc=lca(a[i],a[i+1]);
            b[++len]=a[i];
            b[++len]=lc;
        }
        b[++len]=a[k];
        b[++len]=1;
        rlen=len;
        sort(b+1,b+len+1,cmp);
        for(int i=1;i<len;i++)
        {
            if(b[i]==b[i+1]){rlen--;continue;}
            int lc=lca(b[i],b[i+1]);
            Tr.add(lc,b[i+1],dis(lc,b[i+1]));
            Tr.add(b[i+1],lc,dis(lc,b[i+1]));
        }
        dfsdp(1,0);
        Tr.tot=0;
        printf("%lld\n",dp[1]);
        for(int i=1;i<=len;i++) Tr.head[b[i]]=0,cis[b[i]]=0,dp[b[i]]=0,vis[b[i]]=0;
    }
}

例题

例一 P4606 SDOI2018

先建出圆方树，需要统计任意关键点路径上的点数（去重）。

考虑建虚树，求虚树上父亲儿子两点之间的圆点个数即可。

（这里不用真正连边，利用父子关系统计即可）

#include<bits/stdc++.h>
using namespace std;

const int maxn=2e5+5;

struct Edge
{
    int tot;
    int head[maxn];
    struct edgenode{int to,nxt;}edge[maxn*2];
    void add(int x,int y)
    {
        tot++;
        edge[tot].to=y;
        edge[tot].nxt=head[x];
        head[x]=tot;
    }
    void clr()
    {
        memset(head,0,sizeof(head));
        memset(edge,0,sizeof(edge));
        tot=0;
    }
}Tr,G;

int n,m,cok,tp,tx;
int dfn[maxn],low[maxn],deep[maxn],f[maxn][25],st[maxn],len[maxn],wz[maxn],ed[maxn];

void tarjin(int u)
{
    dfn[u]=low[u]=++cok;
    st[++tp]=u;
    for(int i=G.head[u];i;i=G.edge[i].nxt)
    {
        int v=G.edge[i].to;
        if(!dfn[v])
        {
            tarjin(v);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
            {
                Tr.add(++tx,u);
                Tr.add(u,tx);
                int x=0;
                do
                {
                    x=st[tp--];
                    Tr.add(tx,x);
                    Tr.add(x,tx);
                }while(x!=v);
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
}
void dfs(int u)
{
    len[u]+=(u<=n);
    wz[u]=++cok;
    for(int i=Tr.head[u];i;i=Tr.edge[i].nxt)
    {
        int v=Tr.edge[i].to;
        if(!deep[v])
        {
            deep[v]=deep[u]+1;
            f[v][0]=u;
            len[v]=len[u];
            for(int j=1;j<=20;j++) f[v][j]=f[f[v][j-1]][j-1];
            dfs(v);
        }
    }
    ed[u]=cok;
}
int Lca(int u,int v)
{
    if(deep[u]<deep[v]) swap(u,v);
    for(int i=20;i>=0;i--) if(deep[f[u][i]]>=deep[v]) u=f[u][i];
    if(u==v) return u;
    for(int i=20;i>=0;i--) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
    return f[u][0];
}

int a[maxn];
bool vis[maxn];
bool cmp(int x,int y){return wz[x]<wz[y];}
bool isfa(int u,int v){return st[u]<st[v]&&ed[u]>=ed[v];}

int main()
{
    int _;
    scanf("%d",&_);
    while(_--)
    {
        memset(deep,0,sizeof(deep));
        Tr.clr();
        G.clr();
        memset(dfn,0,sizeof(dfn));
        memset(low,0,sizeof(low));
        memset(f,0,sizeof(f));
        memset(st,0,sizeof(st));
        memset(len,0,sizeof(len));
        memset(wz,0,sizeof(wz));
        memset(ed,0,sizeof(ed));
        cok=tp=tx=0;

        scanf("%d%d",&n,&m);
        tx=n;
        for(int i=1;i<=m;i++)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            G.add(u,v);
            G.add(v,u);
        }

        tarjin(1);
        deep[1]=1;
        len[1]=1;
        cok=0;
        dfs(1);

        int p;
        scanf("%d",&p);
        while(p--)
        {
            int s;
            scanf("%d",&s);
            for(int i=1;i<=s;i++) scanf("%d",&a[i]),vis[a[i]]=1;
            sort(a+1,a+s+1,cmp);
            int sl=s;
            for(int i=1;i<s;i++)
            {
                int lca=Lca(a[i],a[i+1]);
                if(!vis[lca])
                {
                    vis[lca]=1;
                    a[++sl]=lca;
                }
            }
            sort(a+1,a+sl+1,cmp);
            int ans=-2*s;
            for(int i=1;i<=sl;i++)
            {
                int u=a[i],v=a[i%sl+1];
                ans+=len[u]+len[v]-2*len[Lca(u,v)];
            }
            if(Lca(a[1],a[sl])<=n) ans+=2;
            printf("%d\n",ans/2);
            for(int i=1;i<=sl;i++) vis[a[i]]=0;
        }
    }
}

推荐阅读

虚树 - OI Wiki

标签：int,Tr,笔记,学习,edge,maxn,tot,dfn,虚树
From： https://www.cnblogs.com/binbinbjl/p/17992281

相关文章

  • Java学习日记 Day13 好像要摆烂几天
    算法：二叉搜索树的公共祖先：今天就做了一道题，因为要自底向上的查找，所以很像回溯。先递归遍历到最下面的节点，如果当前节点是要找的节点就返回，返回后设置判断条件，判断两个目标节点在同一侧还是在两侧。SpringMVC：后面的异常处理和文件上传没看，看了SSM的整合，基本靠配置文件和注解极大......
  • 【学习笔记】差分约束
    前言2024.1.27\(huge\)在讲不要忽略算法的细节时，以最短路和差分约束为例子。发现自己差分约束忘得差不多了，于是就有了这篇博客。负环在一张图中，若存在一条边权之和为负数的回路，则称这个回路为负环。在一张图中，若存在一条边权之和为正数的回路，则称这个回路为正环。如果一张......
  • (2024.1.22-2024.1.28)C语言学习小结
    本周主要围绕《HeadfirstC》这本书展开C语言学习，按照计划，我学习了前四章的内容。基本内容以下时学习做的思维导图（笔记）第1章虽然做的是思维导图，但实际上因为大多数内容已经掌握，所以实际上就是补充记了几个零散的点。第2、2.5章主要是指针、数组、字符串的内容，大多也已经......
  • perf_event_open 学习 —— 手册学习
    目录参考NAMESYNOPSISDESCRIPTIONArgumentspid和cpugroup_fdflagsperf_event_attrtypesizeconfigkprobe_func,uprobe_path,kprobe_addr,andprobe_offsetsample_period,sample_freqsample_typeread_formatdisabledinheritpinnedexclusiveexclude_userexclude_kernelexclude_hv......
  • 智能车学习笔记/备忘录乱写 | 地平线篇
    前言持续更新中！校内赛打完分到地平线组了，好多新东西，写篇笔记记录。比赛使用OriginBot车模，车模搭载Ubuntu系统。以后估计主要在Ubuntu虚拟机上工作。现在需要先学习ROS2和FoxGlove。一些很基础或者很好记的东西就不写了。常用网址比赛简介（场地、车模、规则等）FoxGlove教程Or......
  • 2024/1/27学习进度笔记
    1)NLP基本概念①NLP（NaturalLanguageProcessing），也就是人们常说的「自然语言处理」，就是研究如何让计算机读懂人类语言，即将人的自然语言转换为计算机可以阅读的指令。②分词是NLP任务的一个起始，分词的好坏会影响整体模型的好坏。并且分词不一样，语义不一样。1.中国北京大......
  • 强化学习是否可以AI4Science呢？
    最近，华为和Google都推出了AI的天气预报系统（发表了nature、science论文，但是没开放公众使用），可以说这个传统的Science问题被AI进行解决以为了传统Science问题是可能被AI解决的。传统的Science问题如果用一个简单的话来进行解释，那就是一个复杂的方程组，可能是高幂次计算的，也可能是偏微分......
  • 1.27学习进度
    1.jieba库可以对中文进行分词2.由于yarn是集群运行，executor可以在所有服务器上执行，所以每个服务器都需要有哦jieba库提供支撑3.如何尽量提高任务计算的资源计算cpu核心和内存量，通过–executor-memory指定executor内存，通过–executor-cores指定executor的核心通过—num-executors指......
  • HTML笔记
    1.HTML笔记1.1HTML文件1.1.1文档声明<!Doctypehtml>1.1.2.基本页面模板<!DOCTYPEhtml><htmllang="en"><head><metacharset="UTF-8"/><!--媒体设置字符集设置--><metaname="viewport"content=&q......
  • MAC地址的格式与分类（学习笔记）
    Mac地址一.明晰概念MAC地址是以太网的MAC子层所使用的地址，是设备在以太网中的物理标识，在以太网中是用来实现多媒体接入控制(MediaAccessControl也是命名的由来）,如同学生的学号，校园内可以通过学号（类似于MAC地址）来找到某个唯一确定的学生。学习时的收获：在学习时尽管查阅了许多......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99