1 引入
首先看这样一道题:[SDOI2011] 消耗战
有一棵树,边上有边权。每次询问给出 \(k\) 个点,找到一些边,使得删去这些边后从 \(1\) 号节点无法达到这 \(k\) 个点中任意一个,同时使边权最小。
显然这是一道树形 dp。如果说只给我们一次询问,可以很简单的 \(O(n)\) 求出。
但是现在有了 \(m\) 次询问,如果再使用这样的方式复杂度就是 \(O(nm)\),显然无法实现。
我们会发现,\(k\) 的数量并不大,如果复杂度达到 \(O(\sum k)\) 级别,也许可以通过。
那么如何实现呢?
2 虚树概念与建立
2.1 概念
假如我们有这样的一张图,其中红色节点就是 \(k\) 个点(称其为关键点):
我们会发现,此时 dp \(1\) 号节点的右子树完全是没有必要的。换句话说,就是这样无谓的 dp 浪费了时间。
我们能不能将 dp 只保留在关键点中呢?这是就要引入虚树。
先看几张图片:
这些节点和边就构成了虚树。
我们发现,虚树并没有改变祖孙关系,也没有遗漏信息(因为保留了关键点的 LCA),只是将原先较大的一棵树变为较小的一棵树。
由此得到虚树定义:保存关键点及所有关键点的 LCA 的树。
现在的问题是:如何建树?
2.2 建树
我们考虑使用单调栈建树。
首先我们考虑之前所学单调栈建树,不难发现单调栈总是在维护树上的一条链。因此考虑维护一个单调递增栈(注意指的是 DFS 序单调递增)。在这个栈中,每个节点在虚树上的父亲就是它栈下面的节点。
首先将所有关键点按照 DFS 序排序,然后将第一个关键点直接加入。
接下来顺次加入每一个关键点。设当前加入的是 \(x\),栈顶元素为 \(t\),同时令 \(l=\text{Lca}(x,t)\)。
接下来我们需要往里面插入这个节点,显然要将不属于这条链上的先取出,取出的同时建边。
什么时候停止呢?设此时栈中第二个元素为 \(p\),当 \(dfn_p\le dfn_l\) 的时候就表明此时已经来到了这条链上。
接下来分类讨论:
- 当 \(l=t\) 时,此时根本不用进行弹栈操作,直接将 \(x\) 加入即可。
- 当 \(l=y\) 时,表明 \(l\) 就在栈内,我们让栈顶连边后弹出(因为它不属于这条链),然后加入 \(x\) 即可。
- 当 \(l\ne y\) 时,表明 \(l\) 此时没有进栈,也就没有和此时的栈顶连边。将栈顶与 \(l\) 连边后弹出,最后加入 \(l\) 和 \(x\) 即可。
这就表明,只要出单调栈就要建边。
最后放三种情况分别表示的图:
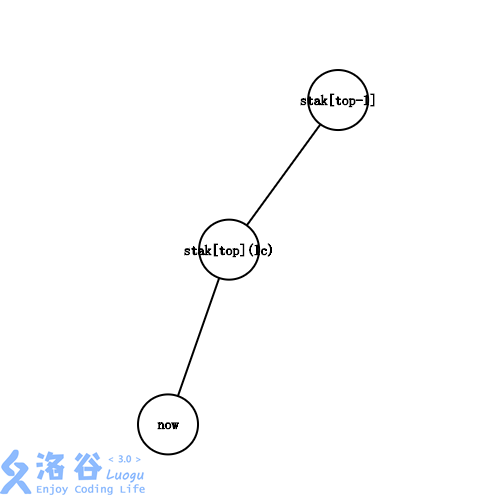
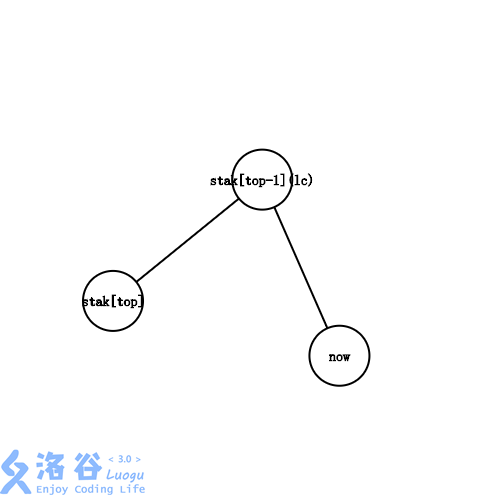
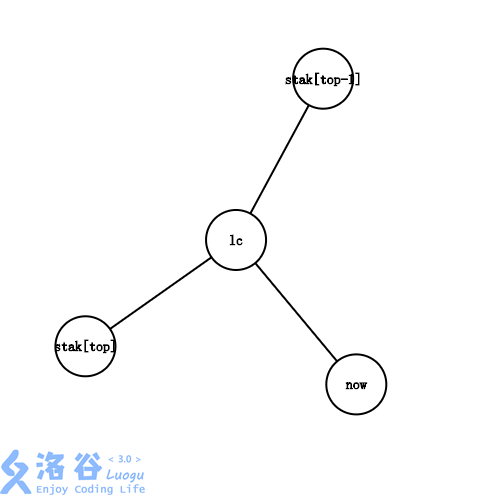
至此你就学会了虚树。
建好虚树之后考的就是树形 dp 了。
2.3 完整代码
//SDOI2011 消耗战
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef long long LL;
const int Maxn = 5e5 + 5;
int n, q, m;
int imp[Maxn];
bool is[Maxn];
int dfn[Maxn], son[Maxn], siz[Maxn], dep[Maxn], fa[Maxn], ind, top[Maxn], minn[Maxn];
struct Tree {
int head[Maxn], edgenum;
struct node {
int nxt, to, w;
}edge[Maxn];
void add(int from, int to, int w) {
edge[++edgenum] = {head[from], to, w};
head[from] = edgenum;
}
void dfs1(int x) {
son[x] = -1;
siz[x] = 1;
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to;
if(to == fa[x]) continue;
fa[to] = x;
dep[to] = dep[x] + 1;
minn[to] = min(minn[x], edge[i].w);
dfs1(to);
siz[x] += siz[to];
if(son[x] == -1 || siz[to] > siz[son[x]]) {
son[x] = to;
}
}
}
void dfs2(int x, int rt) {
top[x] = rt;
dfn[x] = ++ind;
if(son[x] == -1) return;
dfs2(son[x], rt);
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to;
if(to == fa[x] || to == son[x]) continue;
dfs2(to, to);
}
}
int lca(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) {
swap(x, y);
}
x = fa[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
}T;
bool cmp(int x, int y) {
return dfn[x] < dfn[y];
}
struct Virtual_Tree {
int head[Maxn], edgenum;
struct node {
int nxt, to;
}edge[Maxn];
void add(int from, int to) {
edge[++edgenum] = {head[from], to};
head[from] = edgenum;
}
int s[Maxn], top;
void build() {//建树操作
edgenum = top = 0;
s[++top] = imp[1];
head[imp[1]] = 0;
for(int i = 2; i <= m; i++) {
int x = imp[i], t = s[top];
int l = T.lca(x, t);
if(l == t) {
head[x] = 0, s[++top] = x;
continue;
}
while(dfn[s[top - 1]] > dfn[l]) {
add(s[top - 1], s[top]);
top--;
}
if(s[top - 1] != l) {
head[l] = 0, add(l, s[top]);
s[top] = l;
}
else {
add(l, s[top--]);
}
head[x] = 0;
s[++top] = x;
}
for(int i = 1; i < top; i++) {
add(s[i], s[i + 1]);
}
}
int dp[Maxn];
void dfs(int x) {
int cnt = 0;
for(int i = head[x]; i; i = edge[i].nxt) {
int to = edge[i].to;
dfs(to);
cnt += dp[to];
}
if(is[x]) {
dp[x] = minn[x];
}
else {
dp[x] = min(cnt, minn[x]);
}
is[x] = 0;
}
void solve() {
build();
dfs(s[1]);
cout << dp[s[1]] << '\n';
}
}VT;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for(int i = 1; i < n; i++) {
int u, v, w;
cin >> u >> v >> w;
T.add(u, v, w);
T.add(v, u, w);
}
minn[1] = 1e18;
T.dfs1(1);
T.dfs2(1, 1);
cin >> q;
while(q--) {
cin >> m;
for(int i = 1; i <= m; i++) {
cin >> imp[i];
is[imp[i]] = 1;
}
sort(imp + 1, imp + m + 1, cmp);
VT.solve();
}
return 0;
}


