矩阵加速
矩阵加速是数列递推中常用的技巧。当求解的项数巨大时,不妨考虑能否将状态压进矩阵里。
通常,观察出来转移与某一维无关,而这一维恰好很巨大,也就是说同一种转移被做了很多遍的时候,不妨考虑有没有矩阵加速的可能。
P8624 垒骰子
令 \(f_{i,j}\) 表示垒了 \(i\) 个骰子,朝上的一面是 \(j\) 的方案数。枚举 \(36\) 种情况,排除掉互斥的,其余暴力转移。时间复杂度 \(\mathcal{O}(36n)\)。
现在 \(n\leq 10^9\),考虑矩阵优化。令 \(c_{i,j}\) 表示上一个骰子朝上的面为 \(i\) 时,当前骰子朝上的面为 \(j\) 的方案数。如果 \(i\) 与 \(j\) 的对面排斥则有 \(c_{i,j}=0\),否则,由于四个侧面不影响,故有 \(c_{i,j}=4\)。
写出转移方程
\[f_{i,j}=\sum f_{i-1,k}\times c_{k,j} \]写成矩阵的转移形式
\[\begin{pmatrix} f_{i,1} & f_{i,2}&\cdots & f_{i,6} \end{pmatrix} \begin{pmatrix} c_{1,1} & c_{1,2} &\cdots & c_{1,6} \\ c_{2,1} & c_{2,2} &\cdots & c_{2,6} \\ \vdots & \vdots &\ddots & \vdots \\ c_{6,1} & c_{6,2} &\cdots & c_{6,6} \\ \end{pmatrix}= \begin{pmatrix} f_{i+1,1} & f_{i+1,2}&\cdots & f_{i+1,6} \end{pmatrix} \]边界情况 \(f_{1,i}=4\),只需要把中间这个矩阵做 \(n-1\) 次幂即可。
时间复杂度 \(\mathcal{O}(36\log n)\)。
P3193 [HNOI2008] GT 考试
考虑朴素 dp。设 \(f_{i,j}\) 表示前 \(i\) 个数填完,末尾匹配了 \(a\) 的前 \(j\) 个数的方案数。新增一个字符之后,可能出现三种情况:
- 匹配长度 \(+1\)。
- 失配。
- 匹配到了一个更短的前缀。
这个 dp 方法看起来很难优化了。我们换一种思路,令 \(g_{k,j}\) 表示从匹配长度为 \(k\) 通过增加一个字符使得匹配长度变为 \(j\) 的方案数,则有
\[f_{i,j}=\sum f_{i-1,k}\times g_{k,j} \]可以暴力枚举 \(k\) 和最后一个字符,通过 KMP 算出 \(g_{k,j}\) 的值。
会发现转移与 \(i\) 无关,可以写成矩阵形式。
\[\begin{pmatrix} f_{i,0} & f_{i,1}&\cdots & f_{i,m} \end{pmatrix} \begin{pmatrix} g_{0,0} & g_{0,1} &\cdots & g_{0,m} \\ g_{1,0} & g_{1,1} &\cdots & g_{1,m} \\ \vdots & \vdots &\ddots & \vdots \\ g_{m,0} & g_{m,1} &\cdots & g_{m,m} \\ \end{pmatrix}= \begin{pmatrix} f_{i+1,0} & f_{i+1,1}&\cdots & f_{i+1,m} \end{pmatrix} \]时间复杂度 \(\mathcal{O}(m^3\log n)\)。
四边形不等式
若二元函数 \(w(i,j)\) 满足对于任意 \(a\leq b\leq c\leq d\) 都有
\[w(a,c)+w(b,d)\leq w(a,d)+w(b,c) \]则称 \(w\) 满足四边形不等式。
判断 \(w\) 是否满足四边形不等式有几个简单的方法。
- 证明 \(w(i,j)+w(i+1,j+1)\leq w(i,j+1)+w(i+1,j)\)。
- 固定 \(j\) 算出 \(w(i,j+1)-w(i,j)\) 关于 \(i\) 的表达式。如果关于 \(i\) 递减,说明 \(w\) 满足四边形不等式。
如果 \(w(i,j)\) 满足对于任意 \(a\leq b\leq c\leq d\) 都有
\[w(a,d)\geq w(b,c) \]则称 \(w\) 满足区间包含单调。
在二维区间 dp 中,常见如下形式的转移方程。
\[f(i,j)=\min_{i\leq k<j}\{f(i,k)+f(k+1,j)+w(i,j)\} \]我们有如下定理:
- 若 \(w\) 既满足四边形不等式,又满足区间包含单调,则 \(f\) 也满足四边形不等式。
- 若 \(f\) 满足四边形不等式,设 \(f(i,j)\) 的最优决策为 \(s(i,j)\),则有
依据定理,我们可以缩小断点的枚举范围,从而将时间复杂度降至 \(\mathcal{O}(n^2)\)。
对于一些划分型的 dp 方程
\[f(i,j)=\min_{k<i}\{f(k,j-1)+w(k+1,i)\} \]也可以利用四边形不等式优化。
UVA10304 Optimal Binary Search Tree
加强到 \(n\leq 2000\)。
对于这种树形态不确定的 dp 问题,一般都考虑区间 dp,通过枚举树根转移。
设 \(f(i,j)\) 表示用区间 \([i,j]\) 的点构成一棵树的最小代价。枚举树根 \(k\),子树 \([i,k-1]\) 和 \([k+1,j]\) 的度数都增加 \(1\),则有
\[f(i,j)=\max_{i\leq k\leq j} \left\{f(i,k-1)+f(k+1,j)+\sum_{t=i}^je_t\right\} \]直接转移是 \(\mathcal{O}(n^3)\) 的。
令 \(w(i,j)=e_i+e_{i+1}+\cdots +e_j\),容易说明 \(w(i,j)\) 满足区间包含单调。
同时,这种区间和是非常经典的能让四边形不等式取到等号的形式。所以 \(w(i,j)\) 同时满足两个条件,进而 \(f(i,j)\) 满足四边形不等式。
设 \(s(i,j)\) 为令 \(f(i,j)\) 取到最大值的树根 \(k\),从而有
\[s(i,j-1)\leq s(i,j)\leq s(i+1,j) \]时间复杂度优化到 \(\mathcal{O}(n^2)\)。
注意这个题中根节点深度为 \(0\),最后减去所有点权值和即可。
P4767 [IOI2000] 邮局
先对坐标 \(X_i\) 排序。
设 \(f(i,j)\) 表示前 \(i\) 个村庄建 \(j\) 个邮局的答案。枚举上一个村庄覆盖的最远位置 \(k\),钦定放置当前邮局覆盖了 \((k+1,i)\),代价为 \(w(k+1,i)\)。则有
\[f(i,j)=\min_{k< i}\{f(k,j-1)+w(k+1,i)\} \]\(w(i,j)\) 表示用恰一个邮局覆盖 \((i,j)\) 的最小代价,显然将邮局放置在区间中点最优。
考虑从 \(w(i,j-1)\) 递推 \(w(i,j)\),发现加入一个邮局会让区间中点向右偏移一个村庄,此时中点左右村庄距离的变化量两两抵消了。从而有
\[w(i,j)=w(i,j-1)+X_j-X_{\frac{i+j}{2}} \]时间复杂度 \(\mathcal{O}(n^2m)\)。
进一步观察,可以发现 \(w\) 满足区间包含单调。同时,又因为
\[w(i,j)-w(i,j-1)=X_j-X_{\frac{i+j}{2}} \]当 \(i\) 增加时,\(\dfrac{i+j}{2}\) 增加,从而 \(X_j-X_{\frac{i+j}{2}}\) 减小,即 \(w(i,j)-w(i,j-1)\) 关于 \(i\) 递减。
因此 \(w(i,j)\) 满足四边形不等式,进而 \(f(i,j)\) 满足四边形不等式。
设 \(s(i,j)\) 为 \(f(i,j)\) 的最优决策点,则有
\[s(i,j-1)\leq s(i,j)\leq s(i+1,j) \]会发现需要用到 \(f(i+1,j)\) 的最优决策点,所以要倒着转移。
时间复杂度优化到 \(\mathcal{O}(nm)\)。
SP33372 Lannister Army
设 \(f(i,j)\) 为前 \(i\) 个人分成 \(j\) 段的答案。转移可以枚举上一段的结束。
\[f(i,j)=\min_{k<i}\{f(k,j-1)+w(k+1,i)\} \]其中 \(w(i,j)\) 表示区间 \([i,j]\) 的逆序对数。
进一步观察,\(w(i,j)\) 显然有区间包含单调性。又因为
\[w(i,j+1)=\sum_{k=i}^j[a_k>a_{j+1}] + w(i,j) \]\[w(i+1,j+1)=\sum_{k=i+1}^{j}[a_k>a_{j+1}]+w(i+1,j) \]相减能够得到
\[w(i,j+1)-w(i+1,j+1)=w(i,j)-w(i+1,j)-[a_{i+1}>a_{j+1}] \]从而有
\[\begin{aligned} w(i,j+1)+w(i+1,j)&=w(i,j)+w(i+1,j+1)-[a_{i+1}>a_{j+1}] \\ & \leq w(i,j)+w(i+1,j+1) \end{aligned}\]因此 \(w(i,j)\) 满足四边形不等式,进而 \(f(i,j)\) 满足四边形不等式。
设 \(s(i,j)\) 为 \(f(i,j)\) 的最优决策点,则有
\[s(i,j-1)\leq s(i,j)\leq s(i+1,j) \]会发现需要用到 \(f(i+1,j)\) 的最优决策点,所以要倒着转移。
时间复杂度 \(\mathcal{O}(nm)\)。
CF321E Ciel and Gondolas
一样的套路。
设 \(f(i,j)\) 表示前 \(i\) 个人分成 \(j\) 段的答案。枚举上一次分段的结尾 \(k\),可以得到转移方程
\[f(i,j)=\min_{k<i}\{f(k,j-1)+w(k+1,i)\} \]其中 \(w(i,j)\) 表示将区间 \([i,j]\) 的人单独分成一组的代价。可以递推求得
\[w(i,j)=w(i,j-1)+\sum_{k=i}^j a_{k,j} \]预处理一个前缀和就行了。
考虑优化,容易说明 \(w(i,j)\) 满足区间包含单调。同时,又因为
\[w(i,j)-w(i,j-1)=\sum_{k=i}^j a_{k,j} \]这个求和号关于 \(i\) 递减。从而 \(w(i,j)\) 满足四边形不等式。进而 \(f(i,j)\) 满足四边形不等式。
时间复杂度 \(\mathcal{O}(nm)\)。
斜率优化
斜率优化用来优化以下形式的转移方程
\[f(i)=\min_{j<i}\{f(j)+A_j+B_i+C_jD_i\} \]朴素转移 \(\mathcal{O}(n^2)\)。
对式子进行变形
\[f(i)-B_i=\min_{j<i}\{f(j)+A_j+C_jD_i\} \]我们令
\[\left\{ \begin{aligned} y_j&=f(j)+A_j \\ x_j&=C_j \\ k_i&=-D_i \\ b_i&=f(i)-B_i \end{aligned} \right. \]则有
\[b_i=\min_{j<i}\{y_j-k_ix_j\} \]\(k_i\) 为定值,只需要最小化截距 \(b_i\)。
我们把点 \((x_j,y_j)\) 扔到二维平面上,可以感觉到可能的决策点 \(j\) 位于下凸壳上。
用一条斜率为 \(k_i\) 的直线从下往上扫,扫到的切点就是决策点 \(j\)。
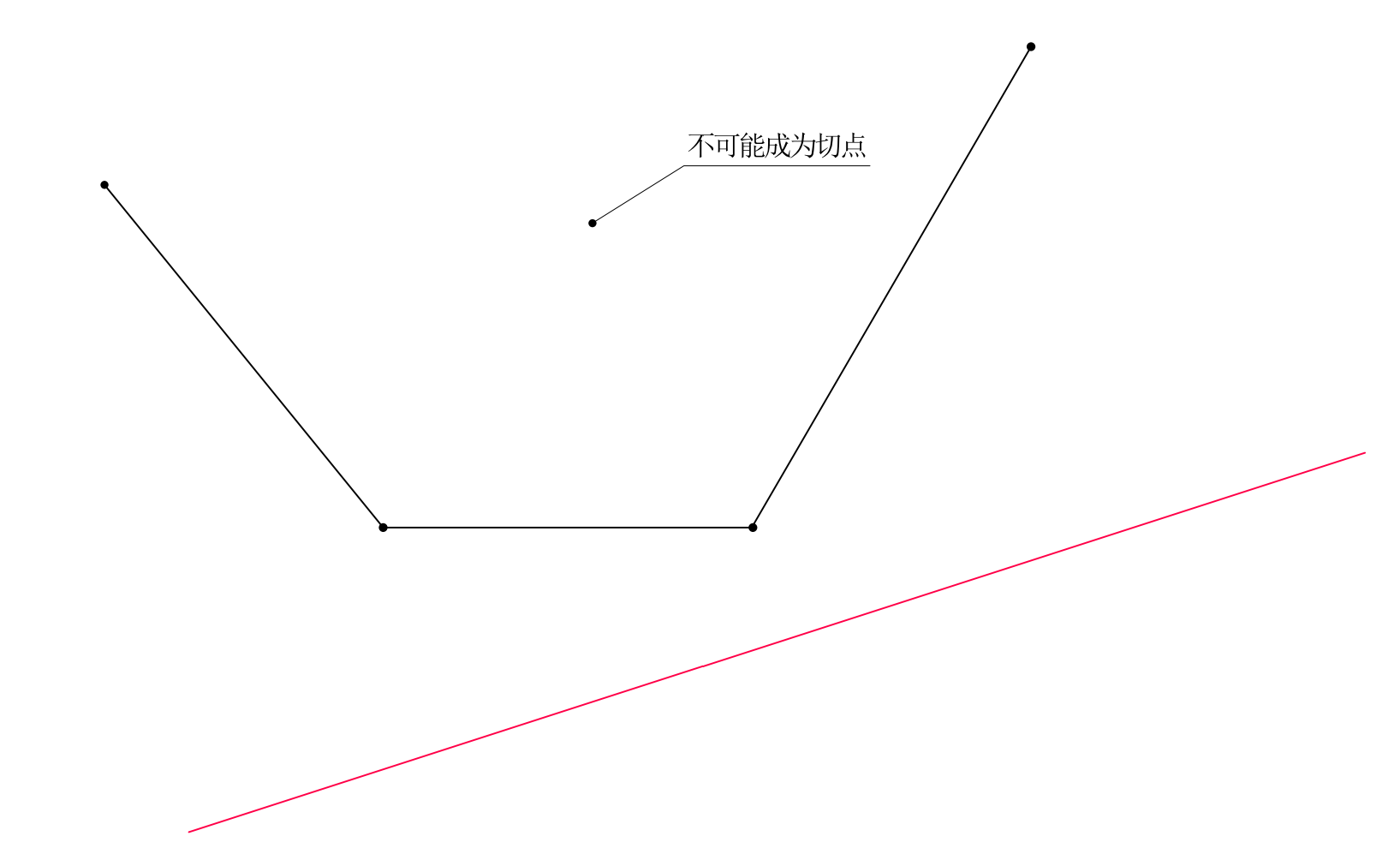
根据几何知识,下凸壳上斜率单调递增,从而决策点 \(j\) 应该是一个分界点,满足 \(j\) 之前斜率 \(k<k_i\),\(j\) 之后斜率 \(k>k_i\)。
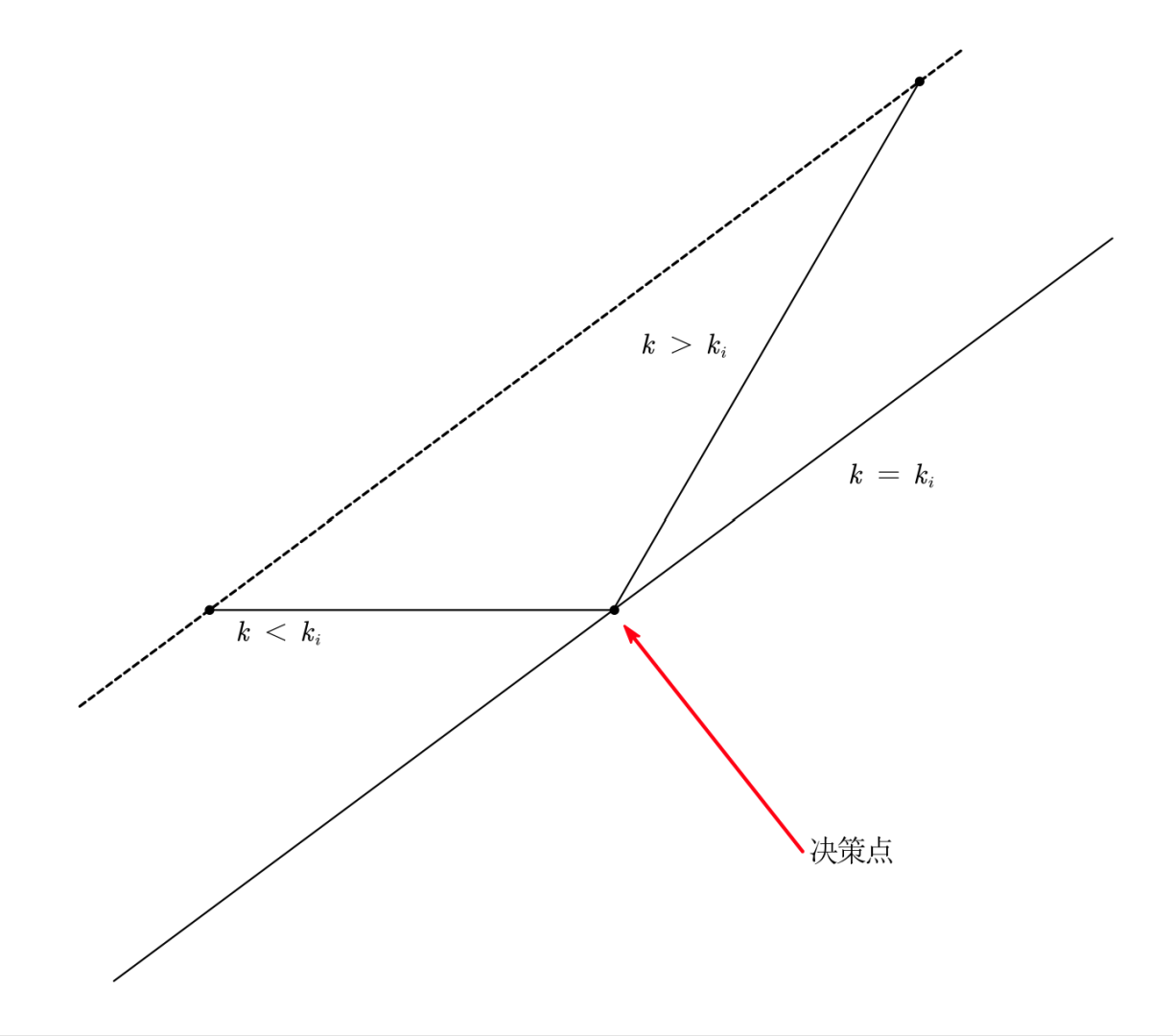
考虑证明这件事情。定义两点 \(j_1,j_2\) 之间的斜率为
\[\operatorname{slope}(j_1,j_2)=\dfrac{y_{j_1}-y_{j_2}}{x_{j_1}-x_{j_2}} \]对于满足 \(x_{j_1}<x_{j_2}\) 的两个点 \(j_1,j_2\),如果 \(j_2\) 比 \(j_1\) 更优,说明
\[y_{j_2}-k_ix_{j_2}<y_{j_1}-k_ix_{j_1} \]移项则有
\[k_i<\dfrac{y_{j_1}-y_{j_2}}{x_{j_1}-x_{j_2}}=\operatorname{slope}(j_1,j_2) \]对于 \(k_i\) 随 \(x_i\) 递增的情况,依据线性规划的角度,可以发现 \(f(i)\) 具有决策单调性。
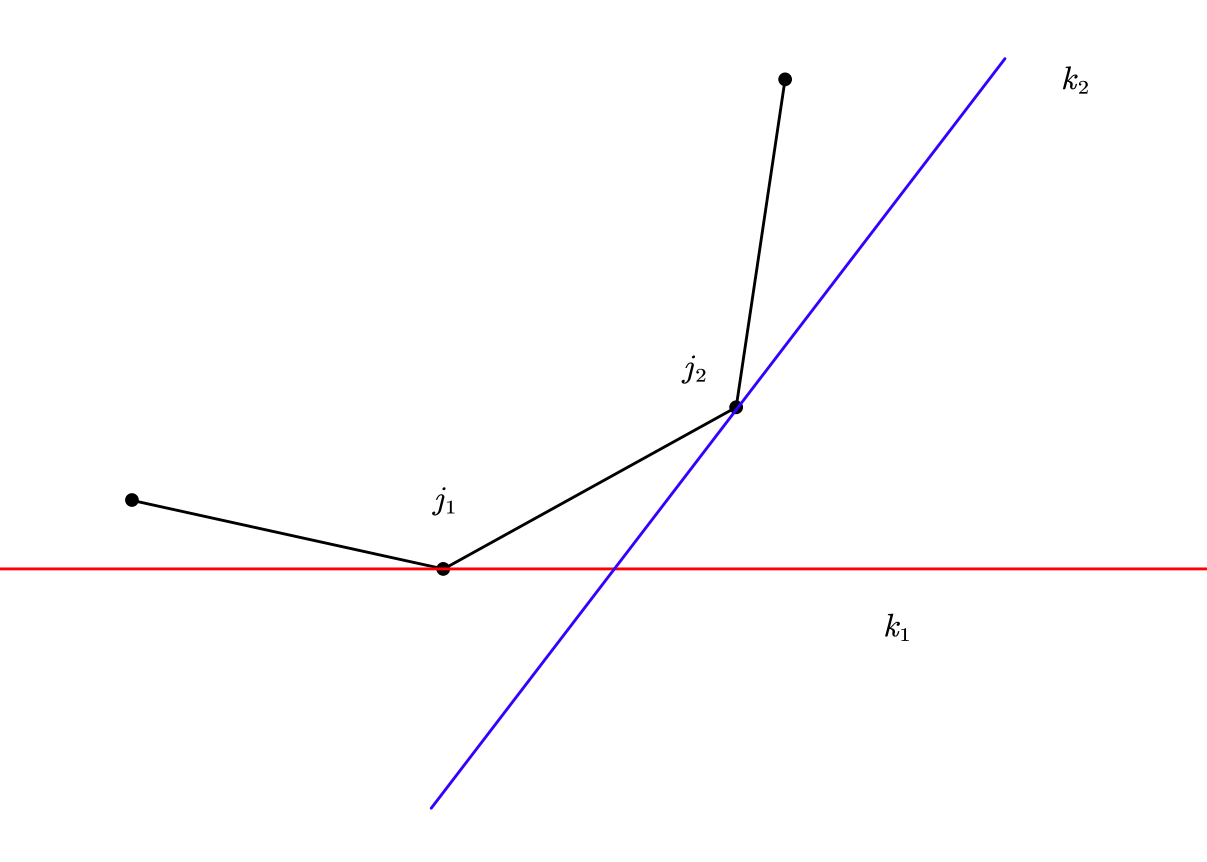
这样,我们可以用一个单调队列维护凸壳。具体来说,当队首两点斜率 \(<k_i\) 时出队,此时的队首 \(j\) 就是决策点。再将队尾两点斜率 \(>k_i\) 的出队,实现动态维护凸壳。\(\mathcal{O}(n)\)。
对于 \(k_i\) 不随 \(x_i\) 递增的情况,可以用单调栈维护斜率,二分出决策点。\(\mathcal{O}(n\log n)\)。
更一般的情况,可以李超线段树。\(\mathcal{O}(n \log n)\)。
P3195 [HNOI2008] 玩具装箱
令 \(f(i)\) 表示将前 \(i\) 个玩具装完的答案。枚举 \(j\),将 \([j+1,i]\) 装到一起转移。
\[f(i)=\min_{j<i}\left\{f(j)+\left(i-j-1+\sum_{k={j+1}}^i C_k-L\right)^2\right\} \]令 \(S_i\) 为 \(C_i\) 的前缀和,则有
\[f(i)=\min_{j<i}\left\{f(j)+\left(i-j-1+S_i-S_j-L\right)^2\right\} \]不妨令 \(A_i=S_i+i\),则有
\[f(i)=\min_{j<i}\left\{f(j)+\left(A_i-A_j-1-L\right)^2\right\} \]我们尝试将 \(i,j\) 分离。将平方项展开
\[f(i)=\min_{j<i}\left\{f(j)+(A_i-1-L)^2+A_j^2-2A_j(A_i-1-L)\right\} \]能提出去的常数提出去
\[f(i)-(A_i-1-L)^2=\min_{j<i}\{f(j)+A_j^2-2A_j(A_i-1-L)\} \]令
\[\left\{ \begin{aligned} y_j&=f(j)+A_j^2 \\ x_j&=2A_j \\ k_i&=A_i-1-L \\ b_i&=f(i)-(A_i-1-L)^2 \end{aligned} \right. \]问题转化为
\[b_i=\min_{j<i}\{y_j-k_ix_j\} \]注意到 \(k_i\) 关于 \(i\) 递增,可以使用斜率优化。
时间复杂度 \(\mathcal{O}(n)\)。
P2120 [ZJOI2007] 仓库建设
从小到达依次建仓库,则之前没有被覆盖的地方都会走到这个仓库里来。
设 \(f(i)\) 表示覆盖了前 \(i\) 个点,且最后一个仓库在第 \(i\) 个点的方案数。
\[f(i)=\min_{j<i}\left\{f(j)+c_i+\sum_{k=j+1}^i p_k(x_i-x_k)\right\} \]令
\[\left\{ \begin{aligned} &S_i=\sum_{j=1}^i p_j \\ &T_i=\sum_{j=1}^i p_jx_j \end{aligned} \right.\]化简转移方程
\[f(i)=\min_{j<i}\left\{f(j)+c_i+x_i(S_i-S_j)-(T_i-T_j)\right\} \]把与 \(j\) 无关的常数提出去
\[f(i)-x_iS_i+T_i-c_i=\min_{j<i}\{f(j)+T_j-x_iS_j\} \]令
\[\left\{ \begin{aligned} y_j&=f(j)+T_j \\ x_j&=S_j \\ k_i&=x_i \\ b_i&=f(i)-x_iS_i+T_i-c_i \end{aligned} \right. \]问题转化为
\[b_i=\min_{j<i}\{y_j-k_ix_j\} \]由于坐标递增,从而 \(k_i\) 关于 \(i\) 递增,可以斜率优化。
时间复杂度 \(\mathcal{O}(n)\)。
注意:算 \(j_1,j_2\) 的斜率一定要用大减小,避免掉负数除负数。不然会出神秘错误。
P3648 [APIO2014] 序列分割
大胆猜测,答案与切割顺序无关。
证明也很好说。设有相邻三块,和分别为 \(a,b,c\)。
- 先切 \(a,b\) 再切 \(b,c\),答案为 \(a\times(b+c)+b\times c=ab+bc+ca\)。
- 先切 \(b,c\) 再切 \(a,b\),答案为 \((a+b)\times c+a\times b=ab+bc+ca\)。
这样就变成了一个从头开始切的问题。
先预处理前缀和 \(S_i\)。设 \(f(i,j)\) 表示前 \(i\) 个切了 \(j\) 刀分成 \(j+1\) 段的答案。
\[f(i,j)=\max_{k<i}\{f(k,j-1)+S_k\times (S_i-S_k)\} \]令
\[\left\{ \begin{aligned} y_k&=f(k,j-1)-S_k^2 \\ x_k&=S_k \\ k_i&=-S_i \\ b_i&=f(i,j) \end{aligned} \right. \]问题转化为
\[b_i=\max_{k<i}\{y_k-k_ix_k\} \]这里的斜率 \(k_i\) 关于 \(i\) 递减,所以要维护的是一个上凸壳。一样可以斜率优化。
时间复杂度 \(\mathcal{O}(nk)\)。
注意斜率不存在的情况。这时候直线是一条竖线,要根据正负判断返回 \(-\infty\) 还是 \(+\infty\)。
P4360 [CEOI2004] 锯木厂选址
只能建两个锯木厂。
先统计出每个点到山脚的距离 \(d_i\)。用后缀和即可。
设 \(f(i)\) 表示只在 \(i\) 点建锯木厂的答案,则有
\[\begin{aligned} f(i)&=\sum_{j=1}^i (d_j-d_i)\times w_j+\sum_{j=i+1}^n d_j\times w_j \\ &= \sum_{j=1}^nd_j\times w_j-d_i\sum_{j=1}^iw_j \end{aligned}\]统计两个前缀和
\[\left\{ \begin{aligned} &S_i=\sum_{j=1}^i w_j \\ &T=\sum_{j=1}^n d_j\times w_j \end{aligned} \right.\]则有
\[f(i)=T-d_i\times S_i \]设 \(g(i)\) 表示在 \(i\) 点建第二个锯木厂的答案。考虑根据 \(f(i)\) 转移
\[g(i)=\min_{j<i}\left\{f(j)-\sum_{k=j+1}^i w_k\times d_i\right\} \]用前缀和化简
\[\begin{aligned} g(i)&=\min_{j<i}\{f(j)-(S_i-S_j)\times d_i\} \\ &=\min_{j<i}\{T-S_jd_j-S_id_i+S_jd_i\} \end{aligned} \]令
\[\left\{ \begin{aligned} y_j&=-S_j\times d_j\\ x_j&=S_j \\ k_i&=-d_i \\ b_i&=g(i)-T+S_id_i \end{aligned} \right. \]问题转化为
\[b_i=\min_{j<i}\{y_j-k_ix_j\} \]注意到 \(k_i\) 关于 \(i\) 递增,可以使用斜率优化。
时间复杂度 \(\mathcal{O}(n)\)。
P3628 [APIO2010] 特别行动队
设 \(f(i)\) 表示将前 \(i\) 个人分组的答案。
\[f(i)=\max_{j<i}\left\{f(j)+a\left(\sum_{k={j+1}}^ix_k\right)^2+b\left(\sum_{k={j+1}}^ix_k\right)+c\right\} \]记 \(S_i\) 为 \(x_i\) 的前缀和,则有
\[f(i)=\max_{j<i}\left\{f(j)+a(S_i-S_j)^2+b\left(S_i-S_j\right)+c\right\} \]把式子展开,将 \(i,j\) 分离。
\[f(i)-aS_i^2-bS_i-c=\max_{j<i}\{f(j)+aS_j^2-bS_j-2aS_iS_j\} \]令
\[\left\{ \begin{aligned} y_j&= f(j)+aS_j^2-bS_j \\ x_j&= S_j \\ k_i&=2aS_i \\ b_i&=f(i)-aS_i^2-bS_i-c \end{aligned} \right. \]问题转化为
\[b_i=\max_{j<i}\{y_j-k_ix_j\} \]由于 \(k_i\) 随 \(i\) 递减,我们要维护上凸壳。可以使用斜率优化。
时间复杂度 \(\mathcal{O}(n)\)。
CF311B Cats Transport
首先发现,每个人一定都有一个“恰好接到某只猫”的目标。否则,让人早出发一段时间,调整至恰好接到路上某只猫,一定不会使答案变劣。
这样,我们可以给每个人钦定一个“恰好接上”的猫的位置,让他走到这里就停,把路上所有没被接走的猫顺路带走。问题转化为一个划分问题。
可以算出想要恰好接走第 \(i\) 只猫出发的时间 \(t_i\)。把所有猫按照 \(t_i\) 排序,相当于要把序列切成 \(p\) 段,使得每一段的代价是该段所有数与该段最大值之差的和。求最小代价。
设 \(f(i,k)\) 表示 \(k\) 个人接走前 \(i\) 只猫的最小代价。则有
\[f(i,k)=\min_{j<i}\left\{f(j,k-1)+\sum_{p=j+1}^i (t_i-t_p)\right\} \]想到前缀和优化。设 \(S_i\) 为 \(t_i\) 的前缀和,则有
\[f(i,k)=\min_{j<i}\{f(j,k-1)+(i-j) \times t_i-(S_i-S_j)\} \]将 \(i,j\) 分离出来。
\[f(i,k)-i\times t_i+S_i=\min_{j<i}\{f(j,k-1)+S_j-j\times t_i\} \]令
\[\left\{ \begin{aligned} y_j&= f(j,k-1)+S_j \\ x_j&= j \\ k_i&=t_i \\ b_i&=f(i,k)-i\times t_i+S_i \end{aligned} \right. \]问题转化为
\[b_i=\min_{j<i}\{y_j-k_ix_j\} \]注意到 \(k_i\) 关于 \(i\) 递增,可以使用斜率优化。
时间复杂度 \(\mathcal{O}(m\log m+mp)\)。记得初始化边界。
P4072 [SDOI2016] 征途
令 \(d_i\) 为第 \(i\) 段的长度,\(v_i\) 表示第 \(i\) 天走的路程。
熟知方差的展开式
\[s^2=\dfrac{1}{m}\sum_{i=1}^m v_i^2-\left(\dfrac{1}{m}\sum_{i=1}^m v_i\right)^2 \]乘以 \(m^2\) 后就是
\[m^2\times s^2=m\sum_{i=1}^m v_i^2-\left(\sum_{i=1}^m v_i\right)^2 \]和的平方是个定值,只需要考虑平方和。
设 \(f(i,k)\) 表示前 \(i\) 段用了 \(k\) 天走完的路程的平方和。
\[f(i,k)=\min_{j<i}\left\{f(j,k-1)+\left(\sum_{p=j+1}^i d_p\right)^2\right\} \]令 \(S_i\) 为 \(d_i\) 的前缀和,则有
\[f(i,k)=\min_{j<i}\left\{f(j,k-1)+\left(S_i-S_j\right)^2\right\} \]展开,变量分离。
\[f(i,k)-S_i^2=\min_{j<i}\left\{f(j,k-1)+S_j^2-2S_iS_j\right\} \]令
\[\left\{ \begin{aligned} y_j&= f(j,k-1)+S_j^2 \\ x_j&= S_j \\ k_i&=2S_i \\ b_i&=f(i,k)-S_i^2 \end{aligned} \right. \]问题转化为
\[b_i=\min_{j<i}\{y_j-k_ix_j\} \]注意到 \(k_i\) 关于 \(i\) 递增,可以斜率优化。
时间复杂度 \(\mathcal{O}(nm)\)。
P5785 SDOI2012 任务安排
设 \(f(i)\) 表示做完前 \(i\) 个任务的代价。但是切了多少段是不确定的,也就是 \(s\) 的贡献不确定。
考虑费用提前计算,在切 \(i\) 时就将 \(s\) 对后面的影响计算了。
\[f(i)=\min_{j<i}\left\{f(j)+\left(\sum_{k=1}^i t_k\right)\left(\sum_{k=j+1}^i c_k\right)+s\left(\sum_{k=j+1}^n c_k\right)\right\} \]统计前缀和,记
\[\left\{ \begin{aligned} &C_i=\sum_{j=1}^i c_j \\ &T_i=\sum_{j=1}^i t_j \end{aligned} \right.\]则有
\[f(i)=\min_{j<i}\{f(j)+T_i\times(C_i-C_j)+s\times(C_n-C_j)\} \]变量分离。
\[f(i)-T_i\times C_i-s\times C_n=\min_{j<i}\{f(j)-(T_i+s)\times C_j\} \]令
\[\left\{ \begin{aligned} y_j&= f(j) \\ x_j&= C_j \\ k_i&=T_i+s \\ b_i&=f(i)-T_i\times C_i-s\times C_n \end{aligned} \right. \]问题转化为
\[b_i=\min_{j<i}\{y_j-k_ix_j\} \]但是会发现,由于 \(t_i\) 可能为负数,这里 \(T_i\) 并不随 \(i\) 递增了。
考虑用单调栈维护一个完整的下凸壳,凸壳上斜率仍然递增,可以对于 \(k_i\) 二分出决策点。
时间复杂度 \(\mathcal{O}(n\log n)\)。
P4027 [NOI2007] 货币兑换
注意到题目最下面给了一个性质:必然存在一种最优的买卖方案满足,每次买进操作使用完所有的人民币,每次卖出操作卖出所有的金券。
设 \(f_i\) 表示第 \(i\) 天能得到的最大钱数,\(r_i\) 为第 \(i\) 天的比例。那么第 \(i\) 天买入可以得到的 \(A,B\) 数量分别为
\[\left\{ \begin{aligned} x_i&=\dfrac{f_ir_i}{a_ir_i+b_i} \\ y_i&=\dfrac{f_i}{a_ir_i+b_i} \end{aligned} \right. \]如果第 \(i\) 天不动,则 \(f_i \leftarrow \max\{f_i,f_{i-1}\}\)。
如果第 \(i\) 天卖出,枚举上一次买入的时间 \(j\),则 \(f_i=\max_{j<i}\{a_ix_j+b_iy_j\}\)。
有两个 \(i,j\) 乘在一起的项,我们提出来一个,变形得到
\[f_i=b_i\times \max_{j<i}\left\{\dfrac{a_i}{b_i}x_j+y_j\right\} \]令直线 \(l_j:x_jx+y_j\),直接上李超线段树维护即可。
由于 \(x=\dfrac{a_i}{b_i}\) 是浮点数,可以先对 \(x\) 离散化一下,李超树上就不用动态开点了。
时间复杂度 \(\mathcal{O}(n \log n)\)。
P2305 [NOI2014] 购票
可以写出一个朴素的转移式子。设 \(d_i\) 为根到 \(i\) 的路径长度,\(j\) 为 \(i\) 的祖先,满足 \(d_i-d_j \leq l_i\),则有
\[f_i=\min\{f_j+(d_i-d_j)p_i+q_i\} \]把式子的项整理一下。
\[f_i-q_i-d_ip_i=\min\{f_j-d_jp_i\} \]令直线 \(l_j:-d_jx+f_j\),可以用李超线段树维护。
先不考虑距离限制,考虑线段树套李超树,对每个节点开一棵李超线段树,查询只需要在 \(i\) 到根链上的所有点的线段之并。
加入距离限制,我们倍增预处理能更新 \(i\) 的最远祖先 \(far_i\),查询的链改为 \(i \sim far_i\) 即可。
树上链查询,可以使用树剖。然而这里有一种更高效简洁的做法。使用出栈序,查询两点之间的信息只需要查询两点出栈序 \([ord_u,ord_v]\) 的线段之并即可。
出栈序的精妙之处在于,看似多考虑了一些不在链上的节点的信息,然而仔细分析可以发现,这些点在 DFS 的过程中还没有被遍历到,线段树上的信息为空,所以这样查询是很精确的。
时间复杂度 \(\mathcal{O}(n \log^2 n)\)。
凸优化
参考博客:奇淫技巧——wqs二分
wqs 二分用来解决一些常规斜率优化不好解决的问题。
回顾斜率优化的基本形式:
\[f(i)=\max_{j<i}\{f(j)+w(j,i)\} \]这里我们并没有给段数做出限制,而 wqs 二分则适用于有段数限制的相同问题。
\[f(i,k)=\max_{j<i}\{f(j,k-1)+w(j,i)\} \]如果第二维很大,斜率优化就不好处理了。
记 \(g(i)\) 表示 \(k=i\) 时的最大收益,如果能用 wqs 二分处理,必须满足
\[g(i+1)-g(i)\leq g(i)-g(i-1) \]也就是 \(g\) 是凸函数。
我们把 \((i,g(i))\) 放到平面上,会构成一个上凸壳,每一点的切线斜率单调递减。我们要求的就是 \(g(k)\)。
二分斜率 \(t\),则过 \((i,g(i))\) 的切线可以写成 \(g(i)=it+b\),截距 \(b=g(i)-it\)。
我们把斜率 \(t\) 看作一次操作的”手续费“,令 \(g'(i)=g(i)-it\),如果规定恰好进行 \(k\) 次操作,得到的最大收益就是 \(g'(k)\),也就是最大化斜率为 \(t\) 的直线的截距。
会发现扣掉所谓”手续费“之后,我们的选择没有段数限制了。这样的 dp 是可以用斜率优化快速完成的。
具体来说,二分斜率 \(t\) 之后,计算最大的截距 \(b\) 以及其在凸壳上的切点 \((i,g'(i))\)。如果 \(i\geq k\),则我们要上调斜率,反之下调斜率。当我们恰好切在 \((k,g'(k))\) 时,就得到了恰好为 \(k\) 的最大收益。
时间复杂度 \(\mathcal{O}(n \log V)\)。
对于下凸壳的情况也是可以做的,只需要将一些判据反转即可。
一种更好理解的方式是,我们把二分的斜率 \(t\) 看作附加权值。对于下凸的函数求最小值,我们令 \(g'(i) \leftarrow g(i)+it\),去掉段数限制求得最优的 \(g'(i)\)。当 \(t\) 太大的时候,我们会倾向于段数更少的取法,从而会导致 \(i<k\),需要把 \(t\) 调小。对于上凸函数求最大值,我们令 \(g'(i)\leftarrow g(i)-it\),调整类似讨论。
P2619 [国家集训队] Tree I
令 \(g(i)\) 表示恰好有 \(i\) 条白色边的最小生成树。打表发现 \((i,g(i))\) 下凸。考虑 wqs 二分。
二分斜率 \(k\),将所有白边的权值 \(+k\),跑一遍 Kruskal 得到最小生成树,统计选了多少条白边。如果选择的数量小于 \(need\),说明权值给大了,向下二分。反之向上二分。
时间复杂度 \(\mathcal{O}(m \log m \log V)\)。
注意到不用每次把所有边都排序,可以将黑白边分别排序,归并合并到一起。可以做到 \(\mathcal{O}(m \log m + m\log V)\)。
P5633 最小度限制生成树
其实就是要从 \(s\) 为端点的边中恰选择 \(k\) 条,跟上一题思想差不多。
这个题好像直接暴力过不了,使用归并实现,时间复杂度 \(\mathcal{O}(m \log m + (n+m)\log w)\)。
有一些神秘的 Corner Case 需要考虑。
P4983 忘情
这个巨大式子其实就是 \((1+\sum x_i)^2\)。设前缀和为 \(S_i\),可以得到朴素的 dp 式子。
\[f(i,k)=\min_{j<i}\left\{f(j,k-1)+(S_i-S_j+1)^2\right\} \]可以感受到,切的段数越多,答案应该越小。所以这个东西应该是下凸的。拆式子之后 wqs 二分即可。
时间复杂度 \(\mathcal{O}(n \log V)\)。
P5308 [COCI2018-2019#4] Akvizna
观察到这个东西正推和反推是一样的,从小往大更方便,不妨倒推。
先忽略掉段数限制,设 \(f_i\) 表示还剩下 \(i\) 个人的最大收益,则有
\[f_i=\max_{j<i}\left\{f_j+\dfrac{i-j}{i}\right\} \]然后这个东西是上凸的,wqs 二分直接上。\(\mathcal{O}(n \log V)\)。
有点卡精度,二分轮数搞多一点。
决策单调性
对于转移方程
\[f(i)=\min_{j<i}\{f(j)+w(j,i)\} \]如果 \(w\) 满足四边形不等式,则 \(f(i)\) 满足决策单调性。
对于最优决策点不降的情况,可以使用单调队列上二分。
对于最优决策点不增的情况,可以使用单调栈上二分。
对于特殊的二维 dp,只在层与层之间转移,同一层之间不转移,每一层转移到下一层的决策点有单调性,可以进行分治。
P3515 [POI2011] Lightning Conductor
分治法例题。
考虑把 \(p\) 单独放在一边。
\[p\geq a_j-a_i+\sqrt{|i-j|} \]只需要
\[p\geq \max_{j=1}^n\left\{a_j-a_i+\sqrt{|i-j|}\right\} \]显然取等时最优。
带着绝对值就很不好,考虑分大小讨论,拆掉绝对值。
\[p_i=\max\left\{\max_{j=1}^i\left\{a_j-a_i+\sqrt{i-j}\right\},\max_{j=i}^n\left\{a_j-a_i+\sqrt{j-i}\right\}\right\} \]前后是一样的。只需要考虑前一半的处理,把序列翻转按照同样的方法处理就可以得到后一半。
令
\[f_j(i)=a_j+\sqrt{i-j} \]把这些函数画在二维平面上,则 \(p_i\) 就是用一根 \(x=i\) 的竖线去截,找到最高交点。
由于 \(\sqrt{x}\) 是单增的,容易说明 \(i\) 越大,截得的交点越高。也就是说,这个东西满足决策单调性。
注意到,求解 \(p_i\) 的过程互不影响。考虑分治。
设当前已经知道区间 \([l,r]\) 的点 \(i\) 的最优决策点 \(j\) 位于区间 \([L,R]\) 内,令 \(m=\left\lfloor\dfrac{l+r}{2}\right\rfloor\),暴力找出 \(p_m\) 的最优决策点 \(s_m\)。由决策单调性,\([l,m-1]\) 的答案应该在 \([L,s_m]\) 中产生,\([m+1,r]\) 的答案应该在 \([s_m,R]\) 中产生。递归下去即可。
时间复杂度 \(\mathcal{O}(n\log n)\)。
P5504 [JSOI2011] 柠檬
二分栈例题。
贡献只和选取的 \(s_0\) 和出现次数 \(t\) 有关。那么,最优的划分一定满足分界点恰好是 \(s_0\),即每一段都是 \([s_0,\cdots,s_0]\)。如果边界不是 \(s_0\),让其单独成段不会使得答案变劣。
考虑 dp。设 \(f(i)\) 表示划分前 \(i\) 个数的答案。则有
\[f(i)=\max_{c_i=c_j}\left\{f(j-1)+c_i\left(\sum_{k=j}^i [c_k=c_i]\right)^2\right\} \]这个求和式可以预处理出来。记
\[S_j=\sum_{i=1}^j [c_i=c_j] \]则有
\[f(i)=\max_{c_i=c_j}\{f(j-1)+c_i(S_i-S_j+1)^2\} \]会发现转移只在相同颜色之间,所以 \(c_i(S_i-S_j+1)^2\) 是关于 \(i\) 递增的。
如果存在 \(j_1<j_2\) 满足 \(j_1\) 是 \(i\) 的最优决策点,那么在 \(i\) 增大的过程中,\(j_2\) 永远不可能是 \(i\) 的最优决策点。单个颜色的决策具有单调性。但是全局上,可能会出现先劣后优的情况。
考虑二分得到 \(j_1\) 比 \(j_2\) 更优的起始时间,设为 \(t(j_1,j_2)\)。
- 如果 \(t(j_1,j_2)\leq t(j_2,i)\),那么 \(j_2\) 就可以踢掉了。因为 \(j_2\) 永远不会成为最优决策。
- 如果 \(t(j_1,j_2)\leq i\),那么 \(j_2\) 也可以踢掉。因为这个时刻 \(j_2\) 已经不如 \(j_1\) 优。
对每种颜色维护一个单调栈,存储所有可能成为最优决策点的位置。向 \(i\) 转移时,令当前栈顶为 \(j_2\),次栈顶为 \(j_1\),进行第一种决策,不断弹掉栈顶。然后先将 \(i\) 入栈,进行第二种决策。最终的栈顶就是最优决策点。
时间复杂度 \(\mathcal{O}(n\log n)\)。
标签:min,leq,斜率,mathcal,aligned,优化,复杂度,DP From: https://www.cnblogs.com/duckqwq/p/18132107