二叉搜索树学习笔记

二叉搜索树学习笔记

\(\frac{11}{20}\)，看来是很难完成了。

这篇笔记大概是为了Splay准备的。

二叉搜索树

只需要了解他的思想，结合图片看就很一目了然。

一种比较唐的数据结构，他可以维护以下东西：

• 插入/删除一个数。
• 查询某个数是否出现。
• 查询全局某个数的前驱/后继。

先考虑每个数只出现一次。

闲话，其实能够发现离散化+权值线段树就能够胜任了。

二叉搜索树的形态大概是，对于每个点有一个键，（在这里我们通常用键作为点的编号），我们规定，对于当前点，它的键为 \(x\) ，我们规定，它的左子树所有点的键值都小于 \(x\)，右子树的所有点都大于 \(x\)，比如说下面这张图。

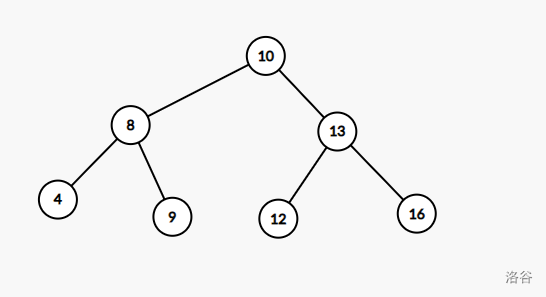
当然你也可以钦定说左边都大于 \(x\)，右边都小于 \(x\)，但是这里不用这种钦定方式。

先考虑操作 \(2\)，如果是查询 \(x\) 是否出现，我们从根开始，如果当前点的键大于 \(x\)，根据定义，那么我们往左子树里面找，否则往右子树里面去找。

查询前驱后继同样的道理。

考虑插入一个数，一样我们根据定义往左/右去走，然后一直到某个点该走的方向没有儿子了，就给他插进去即可。

删除比较复杂，首先我们可以根据定义找到要删的数 \(x\) 的位置，然后因为我们期望删完以后，二叉搜索树的形态是不能变化的，这时候我们的做法是在 \(x\) 的左子树中找到最大的值（容易证明这个最大值一定是在叶子），把它删掉，然后“提到” \(x\) 原来所在的位置即可。

这样做正确的原因，是因为我在左子树里面找到了这个最大值 \(p\)，那么左子树剩余的所有点一定满足小于它，右子树显然也是满足条件的，因为这个点是在左子树里面选出来的。

比如说要删除 \(10\) 的话，我们直接把 \(9\) 提起来到 \(10\) 的位置即可。

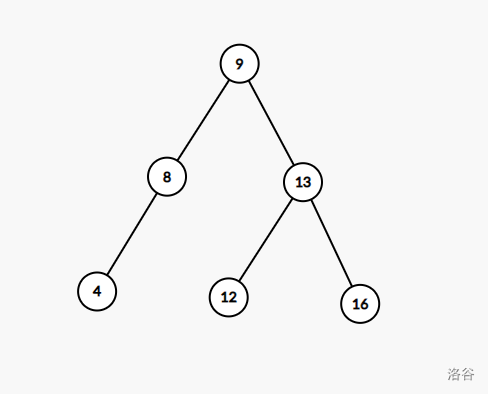
如果数重复的话，对于每个数在维护键的同时，多维护一个次数即可。

树高理论上是 \(O(\log)\) 的样子，时间复杂度看起来是 \(O(n \log n)\)，在上面我们的做法中，每次都能走一层，所以树高是维系这个算法的根本。

但是这玩意很好卡，如果我有一个单调上升的序列，那么树高这时候就会达到 \(O(n)\) 的级别，你每次在找的时候就是 \(O(n)\) 的东西，直接给你退化成 \(O(n^2)\)。

但是我们可以通过一些奇妙的旋转来解决这个问题，但是我不会。

代码没写，因为实际也用不到，只需要了解思想即可。

笛卡尔树

这才是主角，他是一种非常特殊的二叉搜索树。

对于笛卡尔树而言，我们要维护一对键值，键 \(k\) 满足二叉搜索树的性质，值 \(w\) 满足堆的性质。

比如说下面这个就是笛卡尔树，\(k\) 是下标。

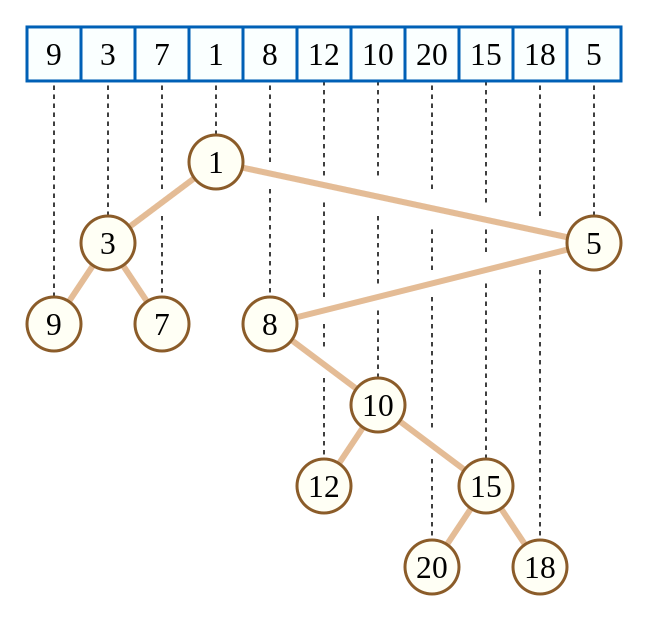
这里我们默认堆是小根堆。

首先考虑建树，他可以在 \(O(n)\) 的时间完成。

考虑先对键值排序，方便维护，我们维护一条“右链”，指的是从根节点开始，不断往右一直到底的一条链。

考虑新加进来一个点 \(x\) 的影响。

• 如果当前点的 \(w\) 已经比末端的 \(w'\) 要大了，那我们直接把这个点接到右链底部点的右端即可。

• 如果不是，我们因为需要满足小根堆的性质，往上找到第一个点 \(p\) 使得满足 \(w'\le w\)，这时候我们钦定 \(x\) 是 \(p\) 的右儿子，然后把 \(p\) 原来的右儿子，变成 \(x\) 的左儿子。这样我们就发现它就完全满足笛卡尔树的性质了。

关于维护这一条右链，我们直接考虑动态的过程，那就应该是维护一个单调栈即可，相当于查询从后往前第一个 \(\le x\) 的数，因为决策点我们可以 \(O(1)\) 判定优/不优。

具体写起来应该也是好写的，还是钦定 \(k\) 作为点的编号，具体做题的时候考虑到什么情况满足堆，什么情况满足二叉搜索树，应该就可以联想到这里。

P1377 [TJOI2011] 树的序

主播练习一道不会。这题我开始考虑的是在建树的过程中动态调整，但是 \(O(n^2)\) 建树还是比较唐的。

考虑静态，我也不知道为什么能想到笛卡尔树。

可能是题目已经给出的 \(a_i\) 满足键的条件了吧，能和二叉搜索树相关的，又看到数据范围，大概想笛卡尔树，也是正确的吧。（可能要是我的话就死挖性质了/yun）

考虑什么可以作为值，发现在建立二叉搜索树的时候，下标自上而下一定是递增的，满足小根堆的性质。

所以我们根据给出的 \(a_i\) 作为键，下标作为值建笛卡尔树，这样保证树的形态不变，且可以 \(O(n)\) 建树。

然后考虑什么时候最优，做前序遍历就可以了，这个可以考虑反证法。