MCE 学习笔记
最小表示法。
你说的对,月考考完了,但是感觉基本炸了。/ll/ll,相对失败。
艹,写了我一个晚上。
\(\frac{3}{20}\),还差的远呢。
闲话:MCE 是 a3 叫的,不过感觉挺好听。
这个算法出题的话可能就比较板了,所以不是很热门?
不废话了。
引入定义:
-
循环同构,对于两个字符串 \(S\) 和 \(T\),如果可以在 \(T\) 中找到一个位置,使得从这个位置开始在这个字符串绕一圈(就把这个字符串看成环),使得他和 \(S\) 相等,那么说明 \(S\) 和 \(T\) 是循环同构的。
-
定义字符串 \(S\) 中从 \(l\) 为起点,\(r\) 为终点的字符顺次连接组成的字符串为 \(S(l,r)\)。
容易发现,能和 \(S\) 构成循环同构的字符串,一定是从 \(S\) 任意一个位置开头,转一圈得到的字符串。(根据定义,\(T\) 复原成 \(S\) 的过程,反过来就是 \(S\) 断开组成 \(T\) 的过程。)
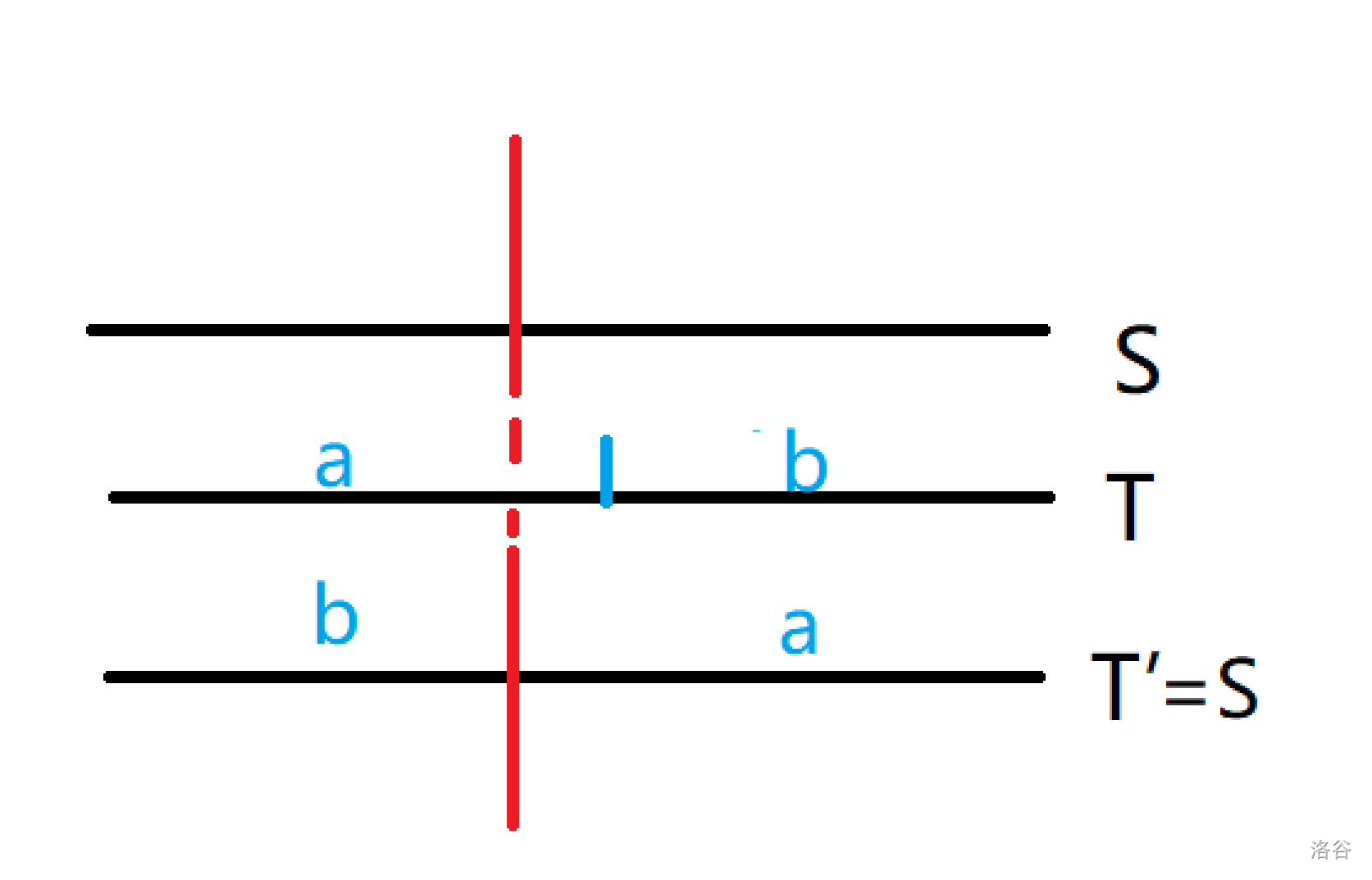
所以,完全可以通过复制两次 \(S\),找到所有和 \(S\) 循环同构的字符串。
最小表示法解决的问题就是,对于 \(S\) 所有与其循环同构的字符串中,找到字典序最小的。
因为这样的字符串只有 \(n\) 个,所以显然有 \(O(n^2)\) 的做法。
但是这个东西,可以 \(O(n)\)。
首先有两个下标 \(i,j\),考虑我们正在比较以 \(i\) 为开头和以 \(j\) 为开头的两个循环同构哪个更优,当前比较了前 \(k\) 位都是一样的。
先提醒一下,对于 \(i\) 这个位置,(包含 \(i\))往后第 \(k\) 个位置是 \(S_{i+k-1}\)。
分类讨论。
- 如果 \(k+1\) 也相同,那么
k++即可。 - 如果不同,假设 \(S_{i+k}<S_{j+k}\),可以发现,以 \(i\) 开头的更优,同时,从 \([j,j+k]\) 所有位置的,都不优。,\(j\) 直接跳到 \(j+k+1\) 即可。
原因显然,如果以 \(i+1\) 和 \(j+1\) 开头比较的话,(就相当于\(S(i,i+k)\)和 \(S(j,j+k)\) 删掉一位。) 到第 \(k+1\) 位 以 \(j+1\) 开头的不优,依此类推,到第 \(k+1\) 位,都是不优的。
时间复杂度证明:可以发现,\(i\) 和 \(j\) 都不会走回头路,类似双指针。那么一个位置最多会被踩两次,时间复杂度为 \(O(n)\)。
讲讲代码,代码比较高妙。
int MCE(){
for(int i=1;i<=n;i++) c[i]=c[i+n]=a[i];
int i=1,j=2;
while(i<=n&&j<=n){
int k=1;
while(k<=n&&c[i+k-1]==c[j+k-1]) k++;
if(k>n) break;
if(c[j+k-1]>c[i+k-1]) j=j+k;
else i=i+k;
if(i==j) j++;
}
return min(i,j);
}
思考两个问题:
-
最后
return min(i,j)的原因?如果 \(i\)(或者 \(j\))是劣的且 \(i\) 跳到 \(i+k\) 后大于 \(n\),跳出循环,这时候原先的 \(i\) 是劣的那个,不能取,且一定大于 \(j\)。(或者说,此时的 \(i\) 根本就没存任何一个位置的答案。) -
if(k>n) break;原因? 这个很厉害。这要满足,如果一个字符串 \(S=T+T+...+T\) 的话,(\(T\) 长度最小。)\(i\) 恰好是 \(T\) 中字典序最小的位置(这个可以反证,如果不是最小的话,在匹配就不能构成连续 \(n\) 个均可以匹配。就是不满足 \(k>n\))。
这个时候 \(j\) 就又恰好移动到了 \(i+m\) 的位置,(这个也可以反证,不然不满足 \(T\) 是长度最小的,证出来发现 \(T=S(i,j-1)\) 才是最小的,和假设矛盾。用UVA10298来理解,就是把 \(S(i,i+n-1)\) 和 \(S(j,j+n-1)\) 上下来看,一直上下拼推一推就行。)进而和从 \(i\) 开始往后的 \(n\) 个字符,都是一样的了,所以 \(i\) 就是最优的。
注意细节,if(i==j) j++,一定要这一步,不然匹配了两个相同位置开头的字符串就一定执行 if(k>n) break,求出来就不是正确答案了。
没有什么习题。
标签:同构,MCE,位置,最小,笔记,学习,开头,字符串 From: https://www.cnblogs.com/JuneFailue/p/18118177