SCC学习笔记

SCC 学习笔记

好听点的话来说，就是强连通分量。

一个有向图，里面任意两个节点之间可以相互到达，我们把它称为一个强连通分量。

Kosaraju

首先，对于一个强连通的图，显然，他的反图也是一个强连通图。（因为原先 \(A\) 可以到 \(B\)，\(B\) 可以到 \(A\)，反过来是一样的）

做法是从任意一个点开始，对正图跑一次 \(dfs\) ，记录时间戳，然后根据时间戳从大到小丢到一个栈里面，然后建反图，从栈顶的点开始跑 \(dfs\) ，跑回当前这个点为止，经过的所有点就是这个强连通图里面的点了。（还要打一下 \(vis\) 标记。）

时间是 \(O(n+m)\)，跑的很快，很好记。缺点是不能跑割顶（点）。

Tarjan

• 前置：dfs 树。

以求割顶举例。

割顶：对于图中有一个点 \(x\) ，如果删去它以及其连边后联通块个数增加，那么 \(x\) 即割顶。

先预处理出来 \(dfn\) 序，核心是求一个 \(low\) 数组。

\(low_x\)：表示从 \(x\) 往上走能连接上最早的祖先的编号。

\(low\) 的计算过程是：

• \(low_u=min(low_u,low_v)\)，也就是从 \(u\) 往儿子走再跳回去，这是对于树边的情况。

• \(low_u=min(low_u,dfn_v)\)，注意，这是是 \(dfn_v\)。原因是我至多只能跳一次，如果是 \(low_v\) ，那就是跳多次，跳多次的话，我从中间断的话，他就不能再到 \(low_v\) 了，就不合法。这是对于反边的情况。

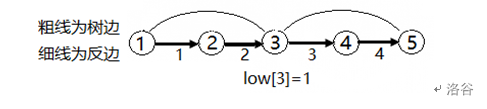
就比如这里。\(low_5=3\) 而不是 \(1\)，原因是如果等于 \(1\) 的话，把 \(3\) 断掉就不能到 \(1\) 了，就不合法。

然后其实就是各种变形就求出不一样的东西来。

比如说割顶，当 \(dfn_u \le low_v\) 时，\(u\) 就是割顶，也就是儿子没有第二条路到当前节点以上，那么断了这个点儿子（及其子树）就到不了当前节点以上，那就是不连通了。

如果 \(dfn_u<low_v\)，该边即割边（桥）。

缩点

强连通分量一个应用。

就是把在一个图内的强连通分量“缩”成一个点，这样可以减少遍历的次数。

在跑 Kosaraju或者 Tarjan 的时候，我们对每一个点记录一个 \(id\)，表示他属于哪一个强连通分量的集合里面。（对每个集合标号）

然后枚举原来图里面所有的边，如果两个点的 \(id\) 不同，说明这两个强连通分量有边可以到达，然后连边即可。

缩点完之后就是图就是 DAG了。那就可以在上面跑 \(dp\)。

边双连通分量/点双连通分量

• 点双连通分量：

定义：任意两个点都能有两条点不重复的路径的无向图就是点双连通分量。

首先就是，点双里面必然没有割点。

如果有的话，桥两端的两个端点只有一条路径能到达，不符合定义。

所以我们只用维护一个栈，遇到割点的时候直接弹出栈里面（非当前割点儿子）的点就是一个点双。

• 边双连通分量：

定义：任意两个点都能有两条边不重复的路径的无向图就是点双连通分量。

相同的，边双里面没有桥。（不然端点一样不符合性质。）

所以我们考虑找到所有的割边并删去。然后对剩下的连通块进行染色即可。