注:此篇一直在讲高斯-约旦消元法。
https://oi-wiki.org/math/numerical/gauss/
相信大家都读过上面那个wiki。
大家其实都看得挺懵的对吧。
今天我就来教一下大家高斯消元。
技术指导:milk,周百万,TB
\(\LaTeX\) 指导:不是你觉得这文章 \(\LaTeX\) 很好吗?所以没有指导。
首先小学知识“加减消元”大家会吧。
那么,加减消元,计算机会吗?
当然,虽然不像我们这样做,但是,我们可以换一种思路。
矩阵记得吗?
把这个方程组弄成一个矩阵。
如:
\[2x_1+3x_2=114 \]\[3x_1+2x_2=191 \]把它变成
\[\begin{bmatrix} 2&3&|&114\\ 3&2&|&191 \end{bmatrix} \]竖线前面是各项系数,后面是结果。

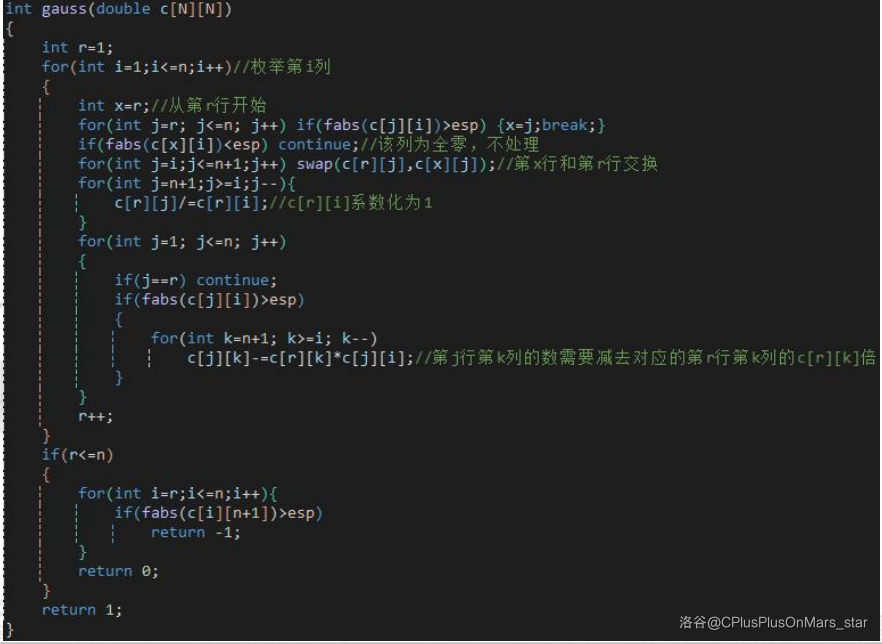
代码实现: