一个很重要的东西
首先为了方便我们规定
\[0^0=1 \]也就是说
\[0^n=\left[n=0\right] \]你们可能会说:“啊火神这个 \([]\) 是啥啊?”
\[[P]称为Iverson括号,P是一个命题,若P为真则[P]=1,否则[P]=0。 \]OIer 话:类似 bool。
这个规定超级有用,有用在哪你们待会就知道了。
朴素集合论
“这玩意跟容斥有什么关系?”
相信这是很多没有学过的人的疑问。
很简单:你待会要用。
定义
\[一个集合是一些对象构成的整体。这些对象称为集合的元素。 \]\[一般采用如下记号: S=\{x|P(x)\} 表示满足性质P的对象构成的集合。 \]很晕对吧?待会你会更晕,建议多读几遍这部分。
集合,但是运算?
\[集合中对象的数量称为集合的大小,记为|S|。 \]\[若x是S中的对象之一,称x属于S,记为x \in S。 \]\[称右边的集合为两集合的交集:A \cap B=\{x|x \in A \land x \in B\} \]\[称右边的集合为两集合的并集:A \cup B=\{x|x \in A \lor x \in B\} \]\[称右边的集合为两集合的差或补:A \setminus B=\{x|x∈A \land x \not\in B\} \]开始步入正轨:组合数
已经自动帮你省流部分:小学数学,杨辉三角。
快感谢我!
唯一要说的是他的记号:
\[\dbinom{n}{m}=\dbinom{n}{n-m}=C_n^m=C_n^{n-m} \]达成挑战:二项式定理(发现二项式定理并学会使用)
\[(1+x)^n=\sum\limits_{i=0}^n\dbinom{n}{i}x^i \]然后是一个重要组合恒等式
它叫 ——Theorem!
\[\sum_{i=0}^{n} (-1)^i\binom{n}{i} =\left [ n=0 \right ] \]容斥,它来辣!
其实挺简单的(?
先来一道辣几题(TB 音)
一次模拟赛,一个班上有 10 个人,5 个人过了 T1,3 个人过了 T2, 1 个人过了两道题,问有多少人过了题。
答案是 5+3-1=7。
waterful 对吧。
结论
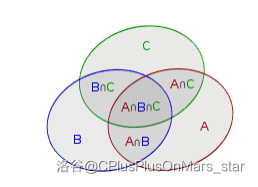
更一般的结论是:
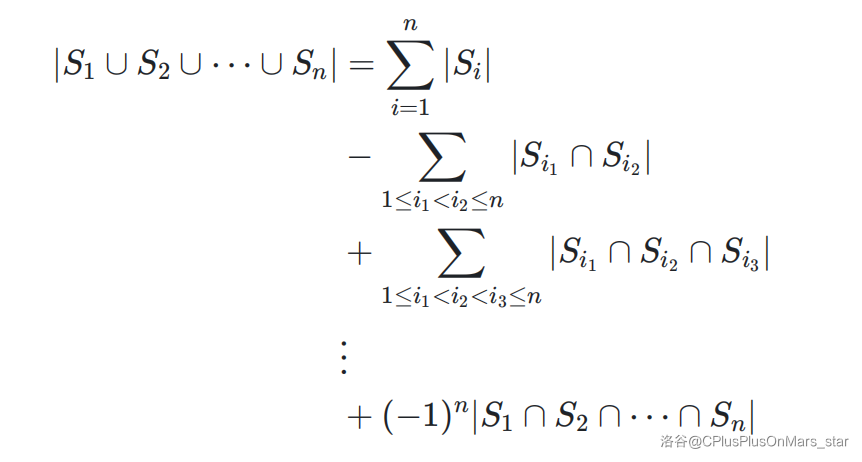
一个难一点的问题
\(现在有n个元素,以及m条限制P_1,P_2,…,P_m,求有多少个元素满足所有的限制。\)
这里介绍“减法原理”:
\[转化为n减去至少违反了一条限制的元素数量。令S_i=\{x|x违反P_i\},那么减去的部分就是所有S_i的并集大小。 \]上一个问题的延伸
全错排问题!是什么我就不说啦(真的只是字面意思)!
提到它不是要解,而是它和上一题几乎一样!
相当于 \(所有全排列数量-有i=p_i的排列数量\)。
再用上“更一般的结论”好吧直接 AC!
k 错排问题的话有了结论读者自证不难。
欧拉函数
待会做题要用。
\(\varphi(n)\) 相当于小于等于 \(n\) 与 \(n\) 互质的数的个数。
\[\varphi(n)=\prod\limits_{}^{}(1-\frac{1}{p_i}) \]例题
https://www.luogu.com.cn/problem/AT_arc101_c
https://www.luogu.com.cn/problem/SP7685
https://www.luogu.com.cn/problem/AT_abc241_h
https://www.luogu.com.cn/problem/AT_abc236_h
标签:www,cn,luogu,容斥,笔记,集合,原理,problem,com From: https://www.cnblogs.com/cppom/p/-/rongchi