动态规划最经典并且在机试中重点考查的问题——背包问题。背包问题的变体繁多,这里主要讨论3种。 0-1背包问题描述的是,有\(n\)件物品,每件物品的重量为\(w[i]\),其价值为\(v[i]\),现在有容量为\(m\)的背包,如何选择物品使得装入背包物品的价值最大。 首先介绍求解这个问题的动态规划方法,其时间复杂度为\(O(nm)\),空间复杂度也为\(O(nm)\)。 设置一个二维数组\(dp[ ][ ]\),令\(dp[i][j]\)表示前\(i\)个物品装进容量为\(j\)的背包能获得的最大价值。那么\(dp[n][m]\)的值就是0-1背包问题的解。 0-1背包的递推式如下: FYI:一般采用下标为1开始存储weight和value,因为我们规定的是下标为i的话是前i件物品,那么默认下标为0的时候是什么物品都没有,是一个空集,这样可以方便我们更加好的进行处理。 完全背包问题和0-1背包问题很像,二者唯一的区别就在于完全背包里面,同一件物品有无穷多件。有\(n\)件物品,每件物品的重量为\(w[i]\),其价值为\(v[i]\),每种物品的数量均为无限个,现在有容量为\(m\)的背包,如何选择物品使得装入背包物品的价值最大? 同样设置一个二维数组\(dp[MAXN][MAXM]\),令\(dp[i][j]\)表示前i个物品装进容量为j的背包能够获得的最大价值。数组\(dp[n][m]\)即为完全背包问题的解。 和0-1背包问题一样,只考虑第i件物品时,可将情况分为是否放入第i件物品两种: 优化空间复杂度,请看这张图修改dp数组和递推式(也可以说是状态转移)。 总之,完全背包问题的特点是每类物品可选的数量为无穷,其解法与0-1背包问题整体保持一致,与其不同的仅为状态更新时的遍历顺序。 每件物品既不是只有1件,又不是无限多件,而是有限个。多重背包问题:有\(n\)种物品,每种物品的重量为\(w[i]\),其价值为\(v[i]\),每种物品的数量为\(k[i]\),现在有个容量为\(m\)的背包,如何选择使得装入背包物品的价值最大。 求解多重背包的方法就是直接转化为0-1背包问题,不过(1)简单粗暴,把有多个同一物品的每一个都看成是相同重量、相同价值的不同物品;(2)是对同种物品进行有技巧地拆分和捆绑,得到不同的组合,使得可以任意想获得几件此个物品,都能用捆绑的组合加一加得到。 注意这个技巧性的拆分:就是类似二进制法拆,最后不满足2的幂次倍的单独捆绑为一个新物品。 不知道咋,我代码AC不了,感觉逻辑没问题,拆分再重新捆绑,记录新物品的数量,眼睛快瞎了,先这样吧。1.0-1背包
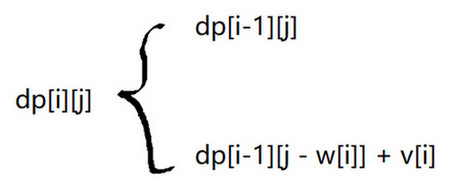

点菜问题
//0-1背包问题 点菜问题 2024-03-17
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 100 + 10;
const int MAXM = 1000 + 10;
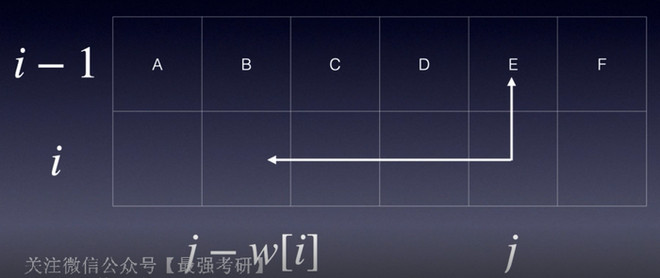
int weight[MAXN];
int value[MAXN];
int dp[MAXN][MAXM];
int main() {
int c, n;//容量为c,物品共n件
while(scanf("%d%d", &c, &n) != EOF) {
for(int i = 1; i <= n; ++i) {
scanf("%d%d", &weight[i], &value[i]);
}
for(int i = 0; i <= n ; ++i) {
dp[i][0] = 0;
}
for(int i = 0; i <= c; ++i) {
dp[0][i] = 0;
}
//考虑第i件物品放入容量为j的背包
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= c; ++j) {
if(j < weight[i]) {
dp[i][j] = dp[i -1][j];
} else {
dp[i][j] = max(dp[i-1][j], dp[i-1][j - weight[i]] + value[i]);
}
}
}
//查表
printf("%d\n",dp[n][c]);
}
return 0;
}
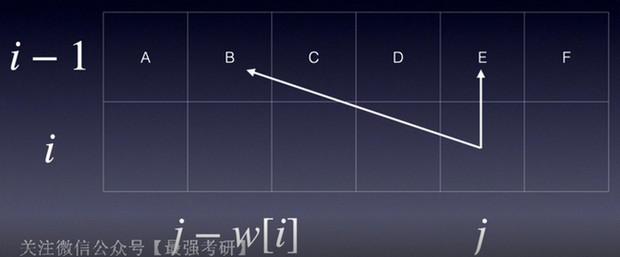
优化空间复杂度-dp设为一维数组
//0-1背包问题 点菜问题-优化空间复杂度 2024-03-17
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 100 + 10;
const int MAXM = 1000 + 10;
int weight[MAXN];
int value[MAXN];
int dp[MAXM];
int main() {
int c, n;//容量为c,物品共n件
while(scanf("%d%d", &c, &n) != EOF) {
for(int i = 1; i <= n; ++i) {
scanf("%d%d", &weight[i], &value[i]);
}
for(int j = 0; j <= c; ++j) {
dp[j] = 0;
}
//考虑第i件物品放入容量为j的背包
for(int i = 1; i <= n; ++i) {
for(int j = c; j >= weight[i]; --j) {
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
//查表
printf("%d\n",dp[c]);
}
return 0;
}
2.完全背包

HDU 4508_减肥记
//完全背包 2024-03-17
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 100 + 10;
const int MAXM = 1e5 + 10;
int weight[MAXN];
int value[MAXN];
int dp[MAXN][MAXM];
int main() {
int n, m;
while(scanf("%d", &n) != EOF) {
for(int i = 1; i <= n; ++i) {
scanf("%d%d", &value[i], &weight[i]);
}
scanf("%d", &m);
for(int i = 0; i <= n; ++i) {
dp[i][0] = 0;
}
for(int j = 0; j <= m; ++j) {
dp[0][j] = 0;
}
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
if(j < weight[i]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = max(dp[i-1][j], dp[i][j - weight[i]] + value[i]);
}
}
}
printf("%d\n",dp[n][m]);
}
return 0;
}
3.多重背包


HDU 2191
/*
* 题目名称:珍惜现在,感恩生活
* 题目来源:HDU 2191
* 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2191
* 代码作者:杨泽邦(炉灰)
*/
#include <iostream>
#include <cstdio>
#include <climits>
using namespace std;
const int MAXN = 100 + 10;
const int MAXM = 1e4 + 10;
int dp[MAXM];
int value[MAXN]; //物品价值
int weight[MAXN]; //物品重量
int amount[MAXN]; //物品数目
int newValue[20 * MAXN]; //拆分后物品价值
int newWeight[20 * MAXN]; //拆分后物品重量
int main() {
int caseNumber;
scanf("%d", &caseNumber);
while (caseNumber--) {
int n, m;
scanf("%d%d", &m, &n); //n件物品,m容量的背包
int number = 0; //分解后物品数量
for (int i = 0; i < n; ++i) {
scanf("%d%d%d", &weight[i], &value[i], &amount[i]);
for (int j = 1; j <= amount[i]; j <<= 1) {
newValue[number] = j * value[i];
newWeight[number] = j * weight[i];
number++;
amount[i] -= j;
}
if (amount[i] > 0) {
newValue[number] = amount[i] * value[i];
newWeight[number] = amount[i] * weight[i];
number++;
}
}
for (int i = 0; i <= m; ++i) {
dp[i] = 0; //初始化
}
for (int i = 0; i < number; ++i) {
for (int j = m; j >= newWeight[i]; --j) {
dp[j] = max(dp[j], dp[j - newWeight[i]] + newValue[i]);
}
}
printf("%d\n", dp[m]);
}
return 0;
}