首页 > 其他分享 >树链剖分【loj模板】(〃＞目＜)

树链剖分【loj模板】(〃＞目＜)

时间：2024-03-12 16:34:22浏览次数：21  
标签：子树 剖分 loj top tr 树链 int dfn 节点

小声吐槽：如果不是拍了200000组没问题后瞪眼瞪出来了，我才不写呢

Decribe:

给定一棵 \(n\) 个节点的树，初始时该树的根为 \(1\) 号节点，每个节点有一个给定的权值。下面依次进行 \(m\) 个操作，操作分为如下五种类型：

  • 换根：将一个指定的节点设置为树的新根。

  • 修改路径权值：给定两个节点，将这两个节点间路径上的所有节点权值（含这两个节点）增加一个给定的值。

  • 修改子树权值：给定一个节点，将以该节点为根的子树内的所有节点权值增加一个给定的值。

  • 询问路径：询问某条路径上节点的权值和。

  • 询问子树：询问某个子树内节点的权值和。

Solution:

讲讲树剖这个东西。树链剖分又分重链剖分、长链剖分、实链剖分。这里只讲重链剖分（下文所讲的树链剖分即重链剖分）。

当遇到树上的区间操作时，尤其是复杂操作，树链剖分绝对是一个不错的选择。它本质上就是把一棵树分割成许多区间，再拼到一起，就可以再套上各种区间数据结构，线段树、ST 表等皆可食用。此外，这玩意常数极小，上界很少能达到，常常创造卡常奇迹，特别香。

好了好了，正式开讲吧，不吹了。首先，对于一棵普普通通的树，一个节点可能会有很多儿子，在区间操作时就不知道要向那个儿子走才是正确的方向，所以一般是让区间的两头向上跳到最近公共祖先，方便统计。但是如何在向上跳的同时计算区间贡献呢？

树链剖分对于每个节点，选择一个子树节点最多的儿子作为重儿子（若有一样多的就随便挑一个，不会有影响），其他儿子作为轻儿子。然后再分割成一条条重链，每条重链的最浅的节点一定是这条链中层数最低的，并且其他节点一定都是重儿子。

比如说这棵树：

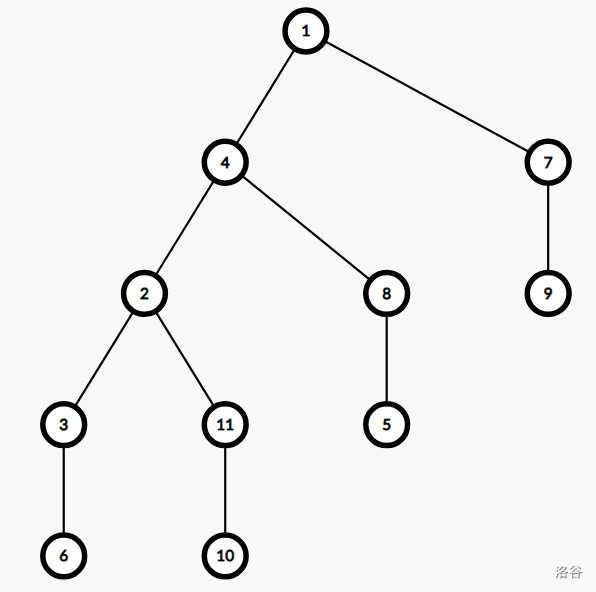
\(1\) 的重儿子就是 \(4\) ，以 \(1\) 为链头的一条可能重链为 $ 1 \to 4 \to 2 \to 3 \to 6 $。所有重链组成的区间就可能是这样的：\(1-4-2-3-6-11-10-8-5-7-9\)，其中 \(1 \to 4 \to 2 \to 3 \to 6\)，\(11\to 10\)，\(8\to 5\)，\(7\to 9\) 为重链。

对于每个节点，我们需要记录以下信息：

  • \(fa\)：节点的父亲。
  • \(dep\)：节点的层数。
  • \(son\)：节点的重儿子。
  • \(siz\)：以该节点为根的子树节点数。
  • \(dfn\)：节点对应区间的位置编号。
  • \(top\)：节点所在重链的链头。

用以实现后面的操作。

将每条重链按一定的顺序拼接起来，就可以用区间数据结构维护了。这样的分链的树有一些有趣的性质：

  • 每下到一个轻儿子，子树节点数至少减少 \(\lceil \cfrac{size}{2} \rceil\)。

这条很简单，如果该儿子的子树节点数超过了 $ \cfrac{size}{2}$，那这个儿子的子树节点数一定比其他儿子的子树节点数多，因而成为重儿子，这与轻儿子的定义不符。

  • 每个子树都在一段连续的区间上。

这两个性质决定了路径操作和子树操作的时间复杂度。第一个性质决定了路径操作不会超过 \(O(\log n)\) 的时间查询路径，第二个性质决定了子树操作是 \(O(1)\) 的。

这里证明一下路径操作不会超过 \(O(\log n)\) 的时间查询路径：

对于路径上左右端点，如果在重链上，可以直接对链头至节点做区间操作。若是不在，则对该链做一次区间操作，并跳到重链头的父亲这个位置，子树节点数因为第一条性质至少增加了 \(\lceil \cfrac{size}{2} \rceil\)，至多能够增加 \(\log n\) 次，因此复杂度为 \(O(\log n)\)。

对于区间修改和查询，随便套个线段树就可以。但 loj 的模板不是一般的恶心。可以看到，题目中还有换根操作，然而树链剖分只能处理静态树，每次换根重分链时间会爆炸的。

实际上，我们并不需要真的换根，只需要处理换根造成的影响即可。

首先，对于路径显然换根是不会有任何影响的。对于子树，我们需要分类讨论。

  1. 根在该子树根上。
    ——那显然是在查询整棵树，对区间 $1 \sim n $ 操作即可。

  2. 根在该子树内。
    ——那就需要查询除根所在的子树内的区间的整个区间，所以我们需要找到根在哪个儿子的子树上。这里就还需要再分类讨论。
    一、根在重儿子所在子树上。那直接将重儿子所在子树的影响去除即可。
    二、根在轻儿子所在子树上。那就从根开始不断跳到重链头，直到父亲是该节点为止。显然同查询路径一样，不会超过 \(O(\log n)\)。

  3. 根在该子树外。
    ——那没有影响，直接对 \(dfn \sim dfn+siz-1\) 这个区间操作即可。

Code：

bool _Start;
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
namespace IO
{
	#define TP template<typename T>
	#define TP_ template<typename T,typename ... T_>
	#ifdef DEBUG
	#define gc() (getchar())
	#else
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	#endif
	#ifdef DEBUG
	void pc(const char &c)
	{
		putchar(c);
	}
	#else
	char pbuf[1<<20],*pp=pbuf;
	void pc(const char &c)
	{
		if(pp-pbuf==1<<20)
			fwrite(pbuf,1,1<<20,stdout),pp=pbuf;
		*pp++=c;
	}
	struct IO{~IO(){fwrite(pbuf,1,pp-pbuf,stdout);}}_;
	#endif
	TP void read(T &x)
	{
		x=0;static int f;f=0;static char ch;ch=gc();
		for(;ch<'0'||ch>'9';ch=gc())ch=='-'&&(f=1);
		for(;ch>='0'&&ch<='9';ch=gc())x=(x<<1)+(x<<3)+(ch^48);
		f&&(x=-x);
	}
	TP void write(T x)
	{
		if(x<0)
			pc('-'),x=-x;
		static T sta[35],top;top=0;
		do
			sta[++top]=x%10,x/=10;
		while(x);
		while(top)
			pc(sta[top--]^48);
	}
	TP_ void read(T &x,T_&...y){read(x);read(y...);}
	TP void writeln(const T x){write(x);pc('\n');}
	TP void writesp(const T x){write(x);pc(' ');}
	TP_ void writeln(const T x,const T_ ...y){writesp(x);writeln(y...);}
	TP void debugsp(const T x){fprintf(stderr,"%d ",x);}
	TP void debug(const T x){fprintf(stderr,"%d\n",x);}
	TP_ void debug(const T x,const T_...y){debugsp(x);debug(y...);}
	TP inline T max(const T &a,const T &b){return a>b?a:b;}
	TP_ inline T max(const T &a,const T_&...b){return max(a,max(b...));} 
	TP inline T min(const T &a,const T &b){return a<b?a:b;}
	TP_ inline T min(const T &a,const T_&...b){return min(a,min(b...));}
	TP inline void swap(T &a,T &b){static T t;t=a;a=b;b=t;}
	TP inline T abs(const T &a){return a>0?a:-a;}
	#undef TP
	#undef TP_
}
using namespace IO;
using std::cerr;
using LL=long long;
constexpr int N=1e5+10;
struct edge
{
	int y,pre;
}
a[N];int alen,last[N];
void ins(int x,int y)
{
	a[++alen]=edge{y,last[x]};
	last[x]=alen;
}
namespace Chain
{
	struct trnode
	{
		int fa,dep,son,siz,dfn,top,end;LL val;//这里 end 就是 dfn+siz-1。
	}tr[N];
	void prepare(int x,int fa)
	{
		tr[x]={fa,tr[fa].dep+1,0,1,0,0,0,tr[x].val};
		for(int k=last[x];k;k=a[k].pre)
		{
			int y=a[k].y;
			if(y==fa)
				continue;
			prepare(y,x);
			tr[x].siz+=tr[y].siz;
			if(tr[tr[x].son].siz<tr[y].siz)
				tr[x].son=y;
		}
	}
	int num,b[N];
	void dfs_chain(int x,int tp)
	{
		b[tr[x].dfn=++num]=x;
		tr[x].top=tp;
		if(tr[x].son)
			dfs_chain(tr[x].son,tp);
		for(int k=last[x];k;k=a[k].pre)
		{
			int y=a[k].y;
			if(y==tr[x].fa||y==tr[x].son)
				continue;
			dfs_chain(y,y);
		}
		tr[x].end=num;
	}
}
namespace Segtree
{
	struct trnode
	{
		int l,r,lc,rc;LL sum;
		LL lazy;
	}
	tr[N<<1];int trlen;
	#define lc tr[now].lc
	#define rc tr[now].rc
	void Plus(int now,LL c)
	{
		tr[now].sum+=(tr[now].r-tr[now].l+1)*c;
		tr[now].lazy+=c;
	}
	void pushup(int now)
	{
		tr[now].sum=tr[lc].sum+tr[rc].sum;
	}
	void pushdown(int now)
	{
		if(tr[now].lazy)
		{
			Plus(lc,tr[now].lazy);
			Plus(rc,tr[now].lazy);
			tr[now].lazy=0;
		}
	}
	void build(int l,int r)
	{
		int now=++trlen;
		tr[now]={l,r};
		if(l==r)
			tr[now].sum=Chain::tr[Chain::b[l]].val;
		else
		{
			int mid=(l+r)>>1;
			lc=trlen+1;build(l,mid);
			rc=trlen+1;build(mid+1,r);
			pushup(now);
		}
	}
	void modify(int now,int l,int r,LL c)
	{
		if(l<=tr[now].l&&tr[now].r<=r)
			return Plus(now,c);
		pushdown(now);
		int mid=(tr[now].r+tr[now].l)>>1;
		if(l<=mid)
			modify(lc,l,r,c);
		if(r>=mid+1)
			modify(rc,l,r,c);
		pushup(now);
	}
	LL query(int now,int l,int r)
	{
		if(l<=tr[now].l&&tr[now].r<=r)
			return tr[now].sum;
		pushdown(now);
		LL ans=0;int mid=(tr[now].r+tr[now].l)>>1;
		if(l<=mid)
			ans+=query(lc,l,r);
		if(r>=mid+1)
			ans+=query(rc,l,r);
		return ans;
	}
	#undef lc
	#undef rc
}
int rt=1;
void modify_route(int x,int y,LL c)
{
	using namespace Chain;
	using Segtree::modify;
	while(tr[x].top!=tr[y].top)
	{
		if(tr[tr[x].top].dep>tr[tr[y].top].dep)
			swap(x,y);
		modify(1,tr[tr[y].top].dfn,tr[y].dfn,c);
		y=tr[tr[y].top].fa;
	}
	if(tr[x].dep>tr[y].dep)
		swap(x,y);
	modify(1,tr[x].dfn,tr[y].dfn,c);
}
void modify_subtree(int x,LL c)
{
	using namespace Chain;
	using Segtree::modify;
	if(tr[x].dfn>tr[rt].dfn||tr[x].end<tr[rt].dfn)
		return modify(1,tr[x].dfn,tr[x].end,c);
	modify(1,1,num,c);
	if(tr[tr[x].son].dfn<=tr[rt].dfn&&tr[tr[x].son].end>=tr[rt].dfn)
		return modify(1,tr[tr[x].son].dfn,tr[tr[x].son].end,-c);
	else if(tr[x].dfn<tr[rt].dfn&&tr[x].end>=tr[rt].dfn)
	{
		int tmp=tr[rt].top;
		while(tr[tmp].fa!=x)
			tmp=tr[tr[tmp].fa].top;
		return modify(1,tr[tmp].dfn,tr[tmp].end,-c);
	}
}
LL query_route(int x,int y)
{
	using namespace Chain;
	using Segtree::query;
	LL ans=0;
	while(tr[x].top!=tr[y].top)
	{
		if(tr[tr[x].top].dep>tr[tr[y].top].dep)
			swap(x,y);
		ans+=query(1,tr[tr[y].top].dfn,tr[y].dfn);
		y=tr[tr[y].top].fa;
	}
	if(tr[x].dep>tr[y].dep)
		swap(x,y);
	ans+=query(1,tr[x].dfn,tr[y].dfn);
	return ans;
}
LL query_subtree(int x)
{
	using namespace Chain;
	using Segtree::query;
	if(tr[x].dfn>tr[rt].dfn||tr[x].end<tr[rt].dfn)
		return query(1,tr[x].dfn,tr[x].end);
	LL ans=0;
	ans+=query(1,1,num);
	if(tr[tr[x].son].dfn<=tr[rt].dfn&&tr[tr[x].son].end>=tr[rt].dfn)
		return ans-=query(1,tr[tr[x].son].dfn,tr[tr[x].son].end);
	else if(tr[x].dfn<tr[rt].dfn&&tr[x].end>=tr[rt].dfn)
	{
		int tmp=tr[rt].top;
		while(tr[tmp].fa!=x)
			tmp=tr[tr[tmp].fa].top;
		return ans-=query(1,tr[tmp].dfn,tr[tmp].end);
	}
	return ans;
}
bool _End;
int main()
{
//	fprintf(stderr,"%.2 MBlf\n",(&_End-&_Start)/1048576.0);
	int n;read(n);
	for(int i=1;i<=n;i++)
		read(Chain::tr[i].val);
	for(int i=2,x;i<=n;i++)
		read(x),ins(x,i);
	Chain::prepare(rt,0);
	Chain::dfs_chain(rt,rt);
	Segtree::build(1,Chain::num);
	int q;read(q);
	while(q--)
	{
		int op;read(op);
		switch(op)
		{
			case 1:
			{
				read(rt);
				break;
			}
			case 2:
			{
				int x,y;LL c;
				read(x,y,c);
				modify_route(x,y,c);
				break;
			}
			case 3:
			{
				int x;LL c;
				read(x,c);
				modify_subtree(x,c);
				break;
			}
			case 4:
			{
				int x,y;
				read(x,y);
				writeln(query_route(x,y));
				break;
			}
			case 5:
			{
				int x;read(x);
				writeln(query_subtree(x));
				break;
			}
		}
	}
	return 0;
}

标签：子树,剖分,loj,top,tr,树链,int,dfn,节点
From： https://www.cnblogs.com/lofty2007/p/18068078

相关文章

  • 树链剖分笔记
    树链剖分+线段树代码量通常在3K左右，出错的地方非常多，为了好好练手，特建立该题单，建议不要进行复制每一题都老老实实重打题单博客题单Orz1.区间加，区间修改，区间最大值#include<bits/stdc++.h>usingnamespacestd;constintMX=1e5+10;intn,m,r,p;intinput[MX]={0};intsiz[......
  • 树链剖分
    树链剖分1基础理论1.1基础概念在树链剖分中，我们将会遇到如下的名词，在此先做以解释：重儿子：对于一个子节点$u$如果$v$是其儿子，且$v$的子树大小是节点$u$的儿子中最大的，则称$v$是$u$的重儿子。轻儿子：除了重儿子以外，就是轻儿子。重链：除顶部以外，其余节点都为重儿子......
  • 树链剖分学习笔记
    树链剖分学习笔记树链剖分的思想及能解决的问题树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。具体来说，将整棵树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。树链剖分（树剖/链剖）有多种形式，如重链剖分，长链剖分和用于Link/cutTree的剖分（......
  • LG5290/LOJ3052 春节十二响 题解(启发式合并)
    考虑当这个东西是一条链的时候我们该怎么做，显然\(1\)​会有两个儿子，然后两个儿子分别是一条链。所以我们可以给两个儿子的链上的所有节点分别加到两个堆里，每次取出两个堆的最大值加入到我们选择的答案中，然后把两个堆的最大值全部pop掉。最终的答案就是我们pop完一个堆之后，......
  • 长链剖分&DP
    长链剖分优化DP长链剖分有一些美妙的性质一个点跳到根最多经过\(\sqrtn\)条链向上跳链，链长一定会增加，最坏是\(1,2,3,...,\sqrtn\)所有长链的总链长相加为n（如说）优化DP如果dp中有一维和深度有关，就考虑优化，考虑用长儿子\(O(1)\)转移（一般是平移，考虑用指针），其他暴力转......
  • LOJ2834 「JOISC 2018 Day 2」修行
    LOJ传送门考虑若已求出钦定\(k\)个升高的排列数量\(f_k\)，那么二项式反演就可以求出恰好\(k\)个升高的排列数量\(g_k\)，即：\[g_k=\sum\limits_{i=k}^n(-1)^{i-k}\binom{i}{k}f_i\]考虑求\(f_i\)。相当于钦定原序列构成了\(n-k\)个上升段。相当于把\(n\)个......
  • 有源汇有上下界最大流 【loj】
    Describe:\(n\)个点，\(m\)条边，每条边\(e\)有一个流量下界\(\text{lower}(e)\)和流量上界\(\text{upper}(e)\)，给定源点\(s\)与汇点\(t\)，求源点到汇点的最小流。Solution：首先因为仍然有流量的限制，第一步就是要找可行流。想到上题无源汇做法，尝试转换。上题中可行流实际......
  • 长链剖分
    谁家刚学会一个知识点就放黑来做啊。长链剖分建议在会重链剖分的基础上再来学长链剖分。长链剖分与重链剖分不同的地方在于：重剖以子树大小来选重儿子，长剖以子树深度来选重儿子。长剖的优势有：可以\(\mathcal{O}(1)\)求\(k\)级祖先，可以在与深度有关的树形dp中优化掉一......
  • P5478 [BJOI2015] 骑士的旅行 - 重链剖分
    首先分析一下题目，对于这棵树，操作如下：查询从X到Y的路径上的前k大的值。把$P_i$上的武力值减去一个$F_i$并在Y上的武力值加上一个$F_i$，再把$P_i$改成Y。将$P_i$上的武力值减去一个$F_i$再加上一个Y，并把$F_i$改成Y。由第一个我们可以想到，先用树剖，再用......
  • P3384 【模板】重链剖分/树链剖分 - SGT && 重链剖分
    本题是非常非常非常纯粹的树剖，利用了重链剖分后下标的性质不多说上代码就好了#include<cstdio>#include<vector>#definelllonglongusingnamespacestd;constintN=1e5+5;intn,m,r;llp,a[N],b[N];vector<int>V[N];intfa[N],dep[N],siz[N],hson[N]......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99