博弈论个人笔记总结

博弈论

简单易懂的博弈论讲解(巴什博弈、尼姆博弈、威佐夫博弈、斐波那契博弈、SG定理) - The_Virtuoso - 博客园 (cnblogs.com)

尼姆博弈（Nim）游戏

引入 ：

• 假设先手为$X$,后手为$Y$
• 先假设有两堆石子，数量分别为 a,b, 如果 $a \neq b\ and\ a >b$ ,$X$选石子$x$个让$a-x = b$ ,然后$Y$只能任选石子个数$k$个导致$a \neq b$,然后$X$跟着$Y$在另外一堆选$k$个,那么还是回到$a = b$,循环那么最终$a = b = 0$,$Y$是没法再取,$Y$失败, 同理如果开局$a = b$ ,则$X$必败
• 在这里 $a = b$为先手必败态，$a\neq b$ 为先手必胜态

推广:

• 假设有n堆石子呢， 我们该怎么办，我们可以想到异或的性质，二进制同位相同异或值为0，否则为1
• 假设有3堆石子数量二进制表示$a = 1100,b = 1001 ,c = 0101$ ,$a$ ^ $b$ ^ $c = 0$
• 正常情况是可以压缩为只有两堆石子那样,$X$取多少,$Y$取多少
• 如果$X$挣扎在$a$石堆中取$1010$,那么剩余的石子堆中$a = 0010,b = 1001,c = 0101$中均没有那么大的数,即$Y$不能取相同的数
• 让 $S = a$^$b$$c$那么$Y$只需要在剩余石堆中寻找符合的( $Value$^S$ \le Value$ 也就是让该石堆的数量为其余石堆的异或值 )即石堆b取掉$b - b$^S,那么$\ \ b -> b$^$S$
• 结束后$a = 0010,b = 0111,c = 0101$,那么再次,$a$ ^ $b$ ^ $c = 0$
• 也就是说如果只要开局$a_1$ ^$a_2$...^$a_n = 0$,不管$X$怎么操作,$Y$永远都可以让$a_1$ ^$a_2$...^$a_n = 0$,直到取完,$X$失败
• 同理开局$a_1$ ^$a_2$...^$a_n \neq 0$,$X$都可以让$a_1$ ^$a_2$...^$a_n \neq 0$,直到取完,$Y$失败

总结 :

• $a_1$ ^$a_2$...^$a_n \neq 0$ 先手必胜态
• $a_1$ ^$a_2$...^$a_n = 0$ 先手必败态

#include<cstdio>
using namespace std;

int k,a[500002];

int main(){
  scanf("%d",&k); 
  int s=0;
  for(int i=1;i<=k;i++)
    scanf("%d",&a[i]), s^=a[i];
    
  if(!s) return puts("lose"),0;
  for(int i=1;i<=k;i++){
    if((a[i]^s)>=a[i]) continue;
    printf("%d %d\n",(a[i]-(a[i]^s)),i);
    a[i]=a[i]^s; break;
  }
  for(int i=1;i<=k;i++) printf("%d ",a[i]);
  return 0;
}

题目 :

• Luogu P2197 【模板】nim 游戏
• Luogu P1247 取火柴游戏
• Luogu P1288 取数游戏 II
• SHOI2008]小约翰的游戏
• NOIP2010 普及组] 三国游戏
• Luogu P1290 欧几里德的游戏
• SHOI2002]取石子游戏|【模板】威佐夫博弈

台阶型 Nim游戏

主要思想 :

• $a_1$ ^$a_3$$a_5$...^$ \neq 0$ 先手必胜态
• $a_1$ ^$a_3$$a_5$...^$ = 0$ 先手必败态

expand :每人每次可以从$[1,d]$堆中各取任意多个石子 ?

1int read(){2      int x=0,f=0,ch;3      while(!isdigit(ch=getchar()))f|=ch=='-';4      while(isdigit(ch))x=(x<<1)+(x<<3)+(ch^48),ch=getchar();5      return f?-x:x;6}cpp

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

int T,n;
int a[1005],b[1005];

int main(){
  cin>>T;
  while(T--){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1);
    for(int i=n;i>=1;i--)b[n-i+1]=a[i]-a[i-1]-1;
    
    int s=0;
    for(int i=1;i<=n;i+=2) s^=b[i];
    
    if(s) puts("Georgia will win");
    else puts("Bob will win");
  }
}

题目 :

• POJ1704 Georgia and Bob

Nim游戏 SG函数

主要思想 :

​ DFS树林 转化为 多堆石堆子

​ 如何转换 ?

​ 因为 parent = MEX{childs...}

​ if parent == 0 : child must >= 0 so child of child must have 0 这棵树一定是没用的

​ else parent != 0 next must < parent => 石堆子

补充 :

• mex运算 这是一个施加于集合的运算，表示求出这个集合中最小的没有出现过的非负整数，比如 mex{0,2,3} = 1,mex{1,2} = 0,mex{} = 0

int f[N];
/*
* 递归运算 :
*    parent =  MEX{childs...}
*    Tree : if root == 0 ,这棵树没有意义
*           if root != 0 ,change => Nim多堆石子问题
* 扩展 : 
*    if parent 和 child 存在一种可推断关系即可转化为 sg问题
*/
int sg(int u){
  if(f[u]!=-1) return f[u];  // 记忆化搜索
  set<int> S; // 把子节点的sg值插入集合
  /* TODO : parent about child connections
  *
  *  for(int i=h[u];i;i=ne[i])  // there is edge
  *    S.insert(sg(to[i]));    // mex运算求当前节点的sg值并记忆/
  */
  for(int i=0; ;i++) 
    if(!S.count(i)) return f[u]=i;
}

题目 :

• LOJ 10243. 移棋子游戏
• 集合型 Nim游戏
• POJ2311 Cutting Game

威佐夫博弈

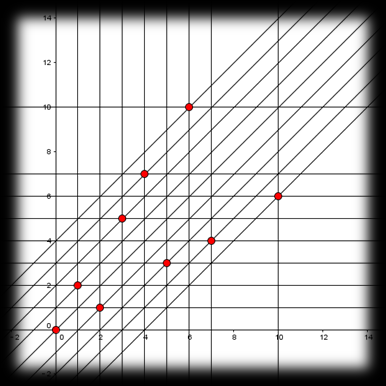
题面 :有两堆各若干个物品，两个人轮流从任一堆取至少一个或同时从两堆中取同样多的物品，

​ 规定每次至少取一个，多者不限，最后取光者得胜。

主要思想 : 枚举

公式 : $\frac{\sqrt{5} + 1}{2} * (n-m) == m .其中 n > m$

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int n,m;
	float eqa=(1+sqrt(5))/2;
	while(cin>>n>>m){
		if(n>m) swap(n,m);
		int dif=m-n;
		if(int(dif*eqa)==n) cout<<"0"<< '\n';
		else cout<<"1"<< '\n';
	}
	return 0;
}
/* 进阶级题型  : win输出 取法 枚举....*/

巴什博奕

题面 : 只有一堆n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个。最后取光者得胜。
主要思想 :

• 什么是博弈论 ? 必胜 => 必败 => 必胜 => ...... , 最终令一个必败
• 那么从小反推到大, cnt <= m 必胜, 怎么由必败态转化来 ? 那就是 在(m+1,2 * m)中只有m+1满足

公式 : $n % (m+1) == 0$

题目 :

• 例题1链接：hdu-1847 Good Luck in CET-4 Everybody!

简单博弈

三种典型的博弈论问题之巴什博奕(Bash Game)_巴什博弈-CSDN博客