首页 > 其他分享 >计算几何——扫描线 学习笔记

计算几何——扫描线 学习笔记

时间：2024-03-11 20:25:29浏览次数：34  
标签：em int 0.5 笔记 kern 扫描线 几何 x2 x1

计算几何——扫描线 学习笔记

你会发现我的笔记的顺序和很多扫描线的讲解是反着来的。

其实是和我老师给的课件完全是逆序（谁帮我算一下逆序对啊喵）。

前言

一开始以为扫描线就是用来求二维几何图像的信息的。

但是其实这个并不准确。个人认为，扫描线其实是一个思想，就像动态规划一样。

具体的，其思想为，用一根（无形的）的线，去扫描一个空间。

在扫描的过程中记录下信息，然后加以处理、应用。如图：

当然你可以暂时忽略这个图片的内容。

引入——会议室问题

问题描述：一个饭店要接待 \(n\) 个顾客，每个顾客会在时间 \([l_i,r_i]\) 内就餐。求饭店里同时存在的最多的顾客数量。

非常基础的一道题了。我们举一个例子：

假设我们有 \(4\) 个顾客，分别记为 \(ABCD\)，我们画出这 \(4\) 个顾客到访的时间段。

\[\begin{array}{lcl} A&:&\kern{4em}|\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}|\\[0.5em] B&:&\kern{2em}|\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}|\\[0.5em] C&:&\kern{11em}|\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}|\\[0.5em] D&:&\kern{1em}|\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}-\kern{-0.5em}|\\[0.5em] \hline\\[-0.5em] &&0\kern{0.5em}1\kern{0.5em}2\kern{0.5em}2\kern{0.5em}3\kern{0.5em}3\kern{0.5em}3\kern{0.5em}2\kern{0.5em}1\kern{0.5em}1\kern{0.5em}0\kern{0.5em}1\kern{0.5em}1\kern{0.5em}1 \end{array} \]

考虑人是怎么思考这一个问题的。

我们一般会从左到右（当然从右到左也是可以的）看完这个时间线，然后直接找到一个时间点，存在最多的线段。显然，这个图里最多有 \(3\) 个顾客。

考虑计算机是怎么实现的。好吧。一样。

考虑一根线从左到右的扫描时间轴，我们发现，当这个线遇到一个线段的左端点（称为入点）的时候，顾客数就会加一，当遇到一个线段的右端点（称为出点）的时候，顾客数就会减一。

于是，我们可以在数轴上标记一个值，记为 \(p_i\)，表示如果扫描线经过这个点，会增加多少。

显然，对于一个顾客 \([l,r]\)，\(p_l=p_l+1,p_r=p_r-1\)。

但是这个算法会有一个问题，就是如果时间轴过于长？

考虑离散化。把数轴压缩。因为我们发现实际上对于这个答案，仅有存在的最多的人数是有用的，区间长度实际上没有用。

于是我们就得到了一个 \(\mathcal O(n)\) 的算法，由于他过于简单，就不写了。

开始——二维数点

先看一道例题：P1972 [SDOI2009] HH的项链。

题目描述：给定长度为 \(n\) 的序列，多组询问，每次询问一个区间 \([l_i,r_i]\)，求这个区间内的不同的数的个数。

显然有莫队和分块的做法。这里讲二维数点的算法。

我们发现，当区间的右端点固定的时候，对于一个数字，其最后一次出现可以作用的范围更大，因此我们贪心的考虑：

记 \(F_i\) 表示为，当前状态下，\(i\) 这个数是否为最后一次出现，即是否计入贡献，记 \(S_i\) 为其前缀和。

固定右端点，考虑每个数最后一次出现的位置所存在的贡献，那么可以知道，区间 \([l,r]\) 内不同的数的个数为 \(\sum_{i=l}^rF_i=S_r-S_{l-1}\)。

然后考虑右端点不固定的情况，我们发现这个右端点向右扩展，是非常容易的。

于是考虑将所有区间离线下来，然后按照右端点排序，从头开始，一个一个扩展右端点。

同时记录下每一个问题的答案。然后考虑这个过程需要怎么维护。

首先，我们需要快速的知道 \(S_x\) 的值，还需要快速的修改任意一个 \(F\) 的值，这就是树状数组！

然后（用扫描线）去扫右端点，就没啥难度了。自己看代码：

#include <bits/stdc++.h>

using namespace std;

#define range(x) x.begin(), x.end()

struct query {
    int id;
    int l, r;
    query() = default;
    query(int id, int l, int r): id(id), l(l), r(r) {}
    friend bool operator <(const query &a, const query &b) { return a.r < b.r; }
};

#define lowbit(x) ((x) & -(x))

constexpr int N = 1e6 + 10;

int n, m;

int s[N];

void add(int x, int v) {
    for (; x <= n; x += lowbit(x)) s[x] += v;
} int sum(int x) {
    int r = 0;
    for (; x; x -= lowbit(x)) r += s[x];
    return r;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> n; vector<int> a(n + 1);
    for (int i = 1; i <= n; ++i) cin >> a[i];
    cin >> m; vector<query> q(m);
    for (int i = 0; i < m; ++i) cin >> q[i].l >> q[i].r, q[i].id = i;
    sort(range(q)); int now = 0;
    vector<int> pos(N), e(m);
    for (query &_ : q) {
        int l = _.l, r = _.r;
        for (int i = now + 1; i <= r; ++i) {
            if (pos[a[i]]) add(pos[a[i]], -1);
            add(i, 1), pos[a[i]] = i;
        } now = r; e[_.id] = sum(r) - sum(l - 1);
    } for (int i : e) cout << i << '\n';
    return 0;
}

入门——二维数点

没错，这个就是真真正正的「二维数点」了。

例题：P2163 [SHOI2007] 园丁的烦恼。

题目描述：给定平面内 \(n\) 个点 \((x_i,y_2)\)，询问一个矩形，求这个矩形内有多少个点。

这道题其实一眼离线、二维查分加离散化（当然这道题数据范围比较小，不需要离散化）。

设 \(S_{a,b}\) 表示 \(\sum_{i=0}^a\sum_{j=0}^bQ_{i,j}\)，其中 \(Q_{i,j}\) 表示 \((i,j)\) 是否有点。

注意到询问 \([x_1,y_1,x_2,y_2]\) 的答案即为 \(S_{x_2,y_2}-S_{x_2,y_1-1}-S_{x_1-1,y_2}+S_{x_1-1,y_1-1}\)。

然后考虑离线怎么处理。

可以将这些分别来看，然后再乘上系数（\(\pm1\)）加到对应的询问里。

因此转化为怎么求所有存在的点 \(S_{a,b}\) 了。

延伸上一题的思路：

按照 \(x\) 左边排序，然后用树状数组维护 \(y\) 轴上是否有点，以及快速前缀求和。

然后扫描，并更新即可。也不难，代码：

#include <bits/stdc++.h>

using namespace std;

#define endl '\n'

using ll = long long;

#define range(x) x.begin(), x.end()

struct point {
    int x, y;
    point() = default;
    point(int x, int y): x(x), y(y) {}
    friend bool operator <(const point &a, const point &b) { return a.x < b.x; }
};

struct query {
    int x, y, v, id;
    query() = default;
    query(int x, int y, int v, int id): x(x), y(y), v(v), id(id) {}
    friend bool operator <(const point &a, const point &b) { return a.x < b.x; }
};

constexpr int N = 1e7 + 10;

int s[N];

#define lowbit(x) ((x) & -(x))

void add(int x, int v) {
    for (; x < N; x += lowbit(x)) s[x] += v;
}

int sum(int x) {
    int r = 0;
    for (; x; x -= lowbit(x)) r += s[x];
    return r;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
    int n, m; cin >> n >> m; vector<point> a(n);
    for (int i = 0; i < n; ++i) cin >> a[i].x >> a[i].y, ++a[i].x, ++a[i].y;
    sort(range(a)); vector<query> q(m << 2);
    for (int i = 0; i < m; ++i) {
        int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
        ++x1, ++y1, ++x2, ++y2;
        q[i] = query(x2, y2, 1, i);
        q[i + m] = query(x1 - 1, y2, -1, i);
        q[i + 2 * m] = query(x2, y1 - 1, -1, i);
        q[i + 3 * 2] = query(x1 - 1, y1 - 1, 1, i);
    } sort(range(q)); vector<int> ans(m);
    int cur = 0; for (int i = m; i < (m << 2); ++i) {
        int x = q[i].x, y = q[i].y, v = q[i].v;
        for (; cur < n && a[cur].x <= x; ++cur) add(a[cur].y, 1);
        ans[q[i].id] += v * sum(y);
    } for (int i : ans) cout << i << endl;
    return 0;
}

基础——亚特兰蒂斯（Atlantis）问题

最经典的扫描线喵：P5490 【模板】扫描线。

题目描述：给出平面内 \(n\) 个矩形的左下以及右上坐标，求出所有矩形构成的图形的面积。

现在假设一根线从下往上扫：

我们可以把整个矩形分成 \(5\)个颜色不同的小矩形。

每个矩形的面积该如何求呢？我们按照 \(y\) 坐标从下往上遍历每个矩形，高也就是相邻的矩形的 \(y\) 坐标的差值，矩形的长度是若干条线段的交集，并且在不断发生变化。

我们使用线段树维护矩形的长度：对于每个矩形，记下面的边为「入边」，上面的边为「出边」。

按照 \(y\) 坐标从下往上遍历每个矩形，入边先被扫描到，将入边加入到线段树，出边后被扫描到，将出边从线段树中删除。对于每一条入边和出边，可以标记为 \(\pm1\)，代表加入和删除。

线段树维护的东西都是点，但是我们需要维护的是区间，那么我们可以把区间下放到点上，也就是每一个叶子节点维护的是一个线段。

维护一个 \(\mathit{cov}\) 为当前区间被几个矩形覆盖，以及一个 \(\mathit{len}\) 表示当前区间被覆盖的区间长度。

我们扫描到一条线，将该条线段加入到线段树维护，修改对应区间的 \(\mathit{cov}\)。

向上更新表示当前区间被覆盖的区间长度，当 \(\mathit{cov}\) 非 \(0\)，则代表整个区间被覆盖；\(\mathit{cov}\) 为 \(0\)，则统计子区间被覆盖的长度

注意到维护的线段，一定是成对出现的，因此不需要标记下传，最后一定会被减回去。

我们根据代码来解释一些细节问题：

  • 下文代码表示的是在标准平面直角坐标系，\(x\) 轴水平向右、\(y\) 轴数值向上，扫描线从下往上扫的。
#include <bits/stdc++.h>

using namespace std;

using ll = long long;

#define range(x) x.begin(), x.end()
  • 头文件等。
struct line {
    int y, x1, x2, v;
    line() = default;
    line(int y, int x1, int x2, int v): y(y), x1(x1), x2(x2), v(v) {}
    friend bool operator <(const line &a, const line &b) { return a.y < b.y; }
};
  • 定义了线段，包括其纵坐标，横坐标上延伸的起始和终止，以及权值。
class segment {

private:

struct emm {
    int l, r;
    int cnt, len;
};

vector<emm> a;
  • 个人习惯，使用 class + struct 定义线段树，标记左端点 \(l\) 及右端点 \(r\)（表示的是原坐标，即未经离散化的，而且注意此处的端点也与普通线段树有区别，是左闭右开的区间，而非闭区间）。
void push_up(int k) {
    if (a[k].cnt) a[k].len = a[k].r - a[k].l;
    else a[k].len = a[k * 2].len + a[k * 2 + 1].len;
}
  • 标记上传，不能全用 else 里的语句的原因是，没有标记下传，只能根据这个区间当前有没有被覆盖来考虑。而如果其两个子区间都被完全覆盖，而其未被标记为完全覆盖，会调用子节点的信息，加起来也是其区间总长度。
void build(vector<int> &p, int k, int l, int r) {
    a[k].l = p[l], a[k].r = p[r];
    a[k].len = a[k].cnt = 0;
    if (r - l == 1) return;
    int mid = l + r >> 1;
    build(p, k * 2, l, mid);
    build(p, k * 2 + 1, mid, r);
}
  • 建树，传入的 \(l\) 和 \(r\) 并不是区间的端点，而是区间端点的离散化的 \(\mathit{rank}\)，需要调用 \(p_i\) 来寻找原坐标，用来标记给线段树维护的区间。而终止条件 r - l == 1 是因为线段树的叶子结点维护的是区间，而非单一的节点，需要两个端点。不需要在这里标记上次的原因是还没有任何有意义的值赋给它。
void modify(int k, int p, int q, int v) {
    int l = a[k].l, r = a[k].r;
    if (l >= p && r <= q) return void((a[k].cnt += v, push_up(k)));
    if (a[k * 2].r > p) modify(k * 2, p, q, v);
    if (a[k * 2 + 1].l < q) modify(k * 2 + 1, p, q, v);
    push_up(k);
}
  • 修改操作，与普通线段树唯一的区别是，修改一个区间仅仅是标记它被完全覆盖，然后标记上传，也就是重新计算这个区间的 \(\mathit{len}\) 值。
public:

segment(vector<int> &p, int n) { a.resize(n << 3); build(p, 1, 1, n); }
void change(int l, int r, int v) { modify(1, l, r, v); }
int xht() { return a[1].len; }

};
  • 没什么意义，只是简化下面调用的代码。
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
    int n; cin >> n;
    vector<line> a(n * 2);
    vector<int> p(n * 2);
    p.push_back(-1);
    for (int i = 0; i < n; ++i) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        p[i] = x1, p[i + n] = x2;
        a[i] = line(y1, x1, x2, 1);
        a[i + n] = line(y2, x1, x2, -1);
    }
    sort(range(a)), sort(range(p));
    int tot = unique(range(p)) - p.begin();
  • 输入和离散化，注意 \(p\) 要加一个极小值（根据题目不同，要比最小坐标值还要小，这道题左边都是非负，因此取 \(-1\) 是可以的，有的还要取更小的值）。
    segment seg(p, tot - 1); ll ans = 0;
    for (int i = 0; i < 2 * n - 1; ++i) {
        seg.change(a[i].x1, a[i].x2, a[i].v);
        ans += 1ll * seg.xht() * (a[i + 1].y - a[i].y);
    } cout << ans << endl;
    return 0;
}
  • 建树和询问。具体的看上面对于小矩阵面积计算的解释。

进阶——矩形周长（Picture）问题

例题：P1856 [IOI1998] [USACO5.5] 矩形周长Picture。

题目描述：给出平面内 \(n\) 个矩形的左下以及右上坐标，求出所有矩形构成的图形的周长。

首先计算横线，不难发现，在扫描线向上平移的时候，增加或者减少的长度就是周长的共线，因为我们的线段是一条一条加的，所以就保证了，加上去，一定是加了一个表面；减去，也一定是减去了一个表面。

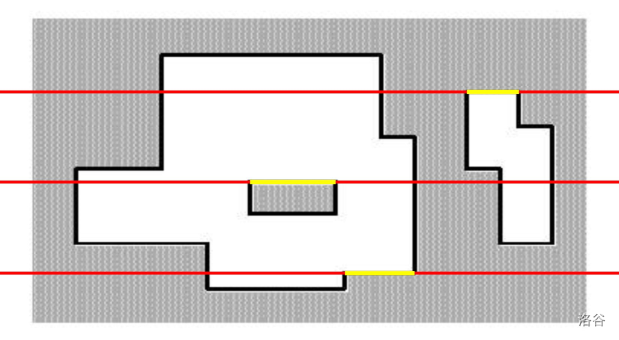
因此对答案的贡献就是上一次获得的长度与这一次的长度的差的绝对值。再解释一下绝对值，因为周长一定是正的，而每次长度变化量就是新增的表面。

所以我们需要加个绝对值。而竖线的长度有两种方法：

  1. 从左到右再扫描一遍。
  2. 扫描横线的过程中，同步记录没有重合的矩形个数，再乘上二就是新增的纵边数，在乘上这个矩形的高度就是新增的竖线的长度了。

作者太菜，只会第一个。

  • 然后我们根据代码再详解一下：
#include <bits/stdc++.h>

using namespace std;

#define range(x) x.begin(), x.end()

using ll = long long;

struct line {
    int y, x1, x2, v;
    line() = default;
    line(int y, int x1, int x2, int v): y(y), x1(x1), x2(x2), v(v) {}
    friend bool operator <(const line &a, const line &b) { return a.y < b.y; }
};

class segment {

private:

struct emm {
    int l, r;
    int cov, len;
};

vector<emm> a;

void push_up(int k) {
    if (a[k].cov) a[k].len = a[k].r - a[k].l;
    else a[k].len = a[k * 2].len + a[k * 2 + 1].len;
}

void build(vector<int> &p, int k, int l, int r) {
    a[k].l = p[l], a[k].r = p[r];
    a[k].cov = a[k].len = 0;
    if (r - l == 1) return;
    int mid = r + l >> 1;
    build(p, k * 2, l, mid);
    build(p, k * 2 + 1, mid, r);
}

void modify(int k, int p, int q, int v) {
    int l = a[k].l, r = a[k].r;
    if (l >= p && r <= q) return void((a[k].cov += v, push_up(k)));
    if (a[k * 2].r > p) modify(k * 2, p, q, v);
    if (a[k * 2 + 1].l < q) modify(k * 2 + 1, p, q, v);
    push_up(k);
}

public:

segment(vector<int> &p, int n) { a.resize(n << 3); build(p, 1, 1, n); }
int xht() { return a[1].len; }
void change(int l, int r, int v) { modify(1, l, r, v); }

};

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
    int n, lt; cin >> n;
  • 从这下面开始才和上一个有本质不同，也就是建了两个扫描线，其中标号 \(1\) 的是向上扫描的，标号 \(2\) 的是向右扫描的。
    vector<line> a1(n * 2), a2(n * 2);
    vector<int> p1(n * 2); vector<int> p2(n * 2);
    p1.push_back(-1e5); p2.push_back(-1e5);
    for (int i = 0; i < n; ++i) {
        int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
        p1[i] = x1, p1[i + n] = x2;
        p2[i] = y1, p2[i + n] = y2;
        a1[i] = line(y1, x1, x2, 1);
        a1[i + n] = line(y2, x1, x2, -1);
        a2[i] = line(x1, y1, y2, 1);
        a2[i + n] = line(x2, y1, y2, -1);
    }
    sort(range(a1)), sort(range(p1));
    sort(range(a2)), sort(range(p2));
    int tot1 = unique(range(p1)) - p1.begin();
    int tot2 = unique(range(p2)) - p2.begin();
    segment seg1(p1, tot1 - 1);
    segment seg2(p2, tot2 - 1);
    ll res = 0; int lt1 = 0, lt2 = 0;
    for (int i = 0; i < 2 * n; ++i) {
        seg1.change(a1[i].x1, a1[i].x2, a1[i].v);
        seg2.change(a2[i].x1, a2[i].x2, a2[i].v);
        int rt1 = seg1.xht(); res += abs(rt1 - lt1);
        int rt2 = seg2.xht(); res += abs(rt2 - lt2);
        lt1 = rt1, lt2 = rt2;
    } cout << res << endl;
    return 0;
}

是不是很简单？

练习题

题单：https://www.luogu.com.cn/training/479926。

Reference

[1] https://oi-wiki.org/geometry/scanning/

[2] https://blog.csdn.net/qq_30320171/article/details/129787418

[3] https://www.luogu.com.cn/article/iilru8ad

[4] https://www.luogu.com.cn/article/9cuyuf44

[5] https://www.youtube.com/watch?v=YnIxejYW7cE

标签：em,int,0.5,笔记,kern,扫描线,几何,x2,x1
From： https://www.cnblogs.com/RainPPR/p/18066950/scanning

相关文章

  • Java学习笔记——第十二天
    面向对象高级（三）内部类内部类是类中的五大成分之一（成员变量、方法、构造器、内部类、代码块），如果一个类定义在另一个类的内部，这个类就是内部类。场景：当一个类的内部，包含了一个完整的事物，且这个事物没有必要单独设计时，就可以把这个事物设计成内部类。比如：汽车类中的发动机类，发动......
  • C++学习笔记
    第一章认识C++1.1命名空间1.1.1命名空间的基本格式命名空间是一个由用户自己定义的作用域，在不同作用域中定义相同变量，不会冲突。命名空间中可以存放以下类型，这些定义/声明在结构体中的内容成为实体变量常量函数（可以是定义或声明）结构体类模板命名空间（可以嵌套定义）......
  • 一文学会JDBC实现java和mySQL的数据连接(尚硅谷学习课程代码+笔记+思路总结)
    JDBC是指数据库连接技术，用于java连接mySQL等数据库。本文详细介绍了尚硅谷课程中JDBC的学习内容和补充知识。概述java语言只提供规范接口，存在于java.sql.javax.sql包下，然后数据库软件根据java提供的规范实现具体的驱动代码（jar)jar包是java程序打成的一种压缩包格式，只要导入就......
  • Vue学习笔记44--mixin混入
    mixin混入：可以理解为是代码的一种重构复用一个混入对象可以包含任意组件选项（如data、methods、mounted等等）。当组件使用混入对象时，所有混入对象的选项将被“混合”进入该组件本身的选项。示例一：局部混合示例局部混入就是在单独的vue组件中引入了mixin混入对象 Student.vue......
  • 【刷题笔记】LeetCode-53 最大子数组和
    题目：给你一个整数数组nums，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。示例1：输入：nums=[-2,1,-3,4,-1,2,1,-5,4]输出：6解释：连续子数组 [4,-1,2,1]的和最大，为 6。示例2:输入：nums=[1]输出：1示例3：输入：nums=[5,4,-1,7,8]输出：23......
  • 技术笔记（6）SourceTree Push到github时报错
    技术笔记（6）SourceTreePush到github时报错remote:SupportforpasswordauthenticationwasremovedonAugust13,2021.Pleaseuseapersonalaccesstokeninstead.​即无法通过输入账号密码的方式来验证，需要使用个人token来验证。昨晚搜到了很多无效方法，搞得有点头痛了，记......
  • 技术笔记（5）MMORPG
    技术笔记（5）MMORPG希望实现的功能或目标：搞定UI系统搞定人物选择系统‍学习笔记：RawImage在登陆界面中负责将某些特定模型渲染出来，比如：人物、怪物UIMask是可以拦截穿透的，即点击上层覆盖的UI界面时，下层是点不到的UISystem类字典：privateDictionary<string,Ba......
  • 载谭 Binomial Sum 学习笔记
    对于微分有限的生成函数\(F(x)\)，有一个生成函数\(G(x)\)，以及数列\(a\)，如果对于\(0\lek\len\)，我们已知\(\displaystyle\sum_{i=0}^na_i[x^i]G(x)^k\)，那么我们能够在\(\Theta(n)\)的时间复杂度内求出\(\displaystyle\sum_{i=0}^na_i[x^i]F(G(x))\)。设\(c=[x^0]......
  • 线段树 学习笔记
    简介略。-1一个模板改编自tourist。其中只需要写apply、pushdown、mergeclasssegtree{public:structnode{//don'tforgettosetdefaultvalue(usedforleaves)//notnecessarilyneutralelement!intsum=0,add=0;voi......
  • 狂神说Java——Mybatis学习笔记
    前言：配合狂神老师的教学视频使用效果更佳：https://www.bilibili.com/video/BV1NE411Q7Nx/?spm_id_from=333.1007.top_right_bar_window_custom_collection.content.click&vd_source=4c3c519d33c113799489c7417a0a4c0e1、简介环境说明：jdk8+MySQL5.7.19maven-3.6.......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99