基础数论学习笔记

1.辗转相减

利用辗转相减法求最大公约数, 即 \(gcd(a, b)\)。假设 \(a > b\), 则 gcd(a, b) =gcd(a − b, b), 不断的利用大的数减去小的数，就能得到最大公约数。

1.证:若\(n,m(n>m)\)互质，则 $(n-m) , m $互质

若不互质,则设 \(n - m = k * a , m = k * b\)

\(\therefore n-k*b=k*a\)

\(\therefore n=k*(a+b)\)，与n,m互质矛盾,得证

我们发现当 a 一直大于 b 的时候，就会一直减去 b，其实就是变成 a%b，所以就变成了辗转相除

2.扩展欧几里得(exgcd)

若\(a,b\)是整数,且\(gcd(a,b)=k\)，那么对于任意的整数\(x,y,ax+by\)都一定是k的倍数。

证：一定存在整数\(x,y\)，使\(ax+by=gcd(a,b)\)成立。

不太好证，采用数形结合的方法

皮克定理 : 给定顶点坐标均是整点（或正方形格点）的简单多边形，面积\(S\)和内部格点数目\(n\)、多边形边界上的格点数目\(k\)：\(S=n+\frac{k}{2} -1\)

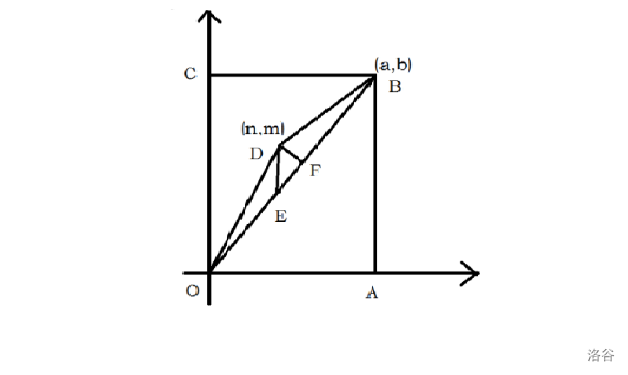
\(\because \gcd(a, b)=1\)

\(\therefore AO\)上无整点

在矩形\(ABCO\)中找离\(AO\)最近的格点\(P(n,m)\)

\(\Delta A P O\) 边界上和内部无整点(如果有的话那个点肯定跟优,与假设矛盾)

\(\therefore S\Delta A P O=0+\frac{3}{2}-1=\frac{1}{2}\)

$\because AO=\sqrt{a^2+b2} $

\(\therefore PH=\frac{\left |bn-am \right |}{\sqrt{a^2+b^2} }\) (点到直线距离公式)

\(\therefore S\Delta A P O=\frac{1}{2}\sqrt{a^2+b^2} *\frac{\left |bn-am \right |}{\sqrt{a^2+b^2} }=\frac{1}{2}\left |bn-am \right |\)

\(\therefore \left |bn-am \right |=1\)

所以当$\left{\begin{matrix}
x=m \
y=-n
\end{matrix}\right. \(或\)\left{\begin{matrix}
x=-m \
y=n
\end{matrix}\right. $时等式成立

所以当 c 是 gcd(a, b) 的倍数的时候,方程有解，将x,y同时扩大多少倍即可

若\(b*x_{1}+a \bmod b *y_{1}=\gcd(a, b)\)

\(\therefore b*x_{1}+(a-\left \lfloor \frac{a}{b} \right \rfloor *b) *y_{1}=\gcd(a, b)\)

\(\therefore a*y_{1}-b*(x_{1}-\left \lfloor \frac{a}{b} \right \rfloor *y_{1}) =\gcd(a, b)\)

\(\therefore x=y1,y=x_{1}-\left \lfloor \frac{a}{b} \right \rfloor *y_{1}\)

3.乘法逆元

设$ \frac{a}{b} \bmod p = x $

$\therefore \frac{a}{b} \equiv x \bmod p $

$\therefore a \equiv bx \pmod{p} $

设 \(a \bmod p=k_{1}.....n\)

$ bx \bmod p=k_{2}.....n$

\(\therefore k_{1}*p+n=a,k_{2}*p+n=bx\)

\(\therefore k_{2}*p+a-k_{1}*p=bx\)

$\therefore a+p*(k_{2}-k_{1})=bx $

$\therefore p*(k_{1}-k_{2})+bx=a $

既然a,b,p都知道，我们就可以用exgcd啦

4.高斯消元

非常好理解，之前我被 @【数据删除】称为高斯消元高手，为了不负期望，我决定复习一次。

#include<iostream>
using namespace std;
int n,st;
double a[105][105];//第i个方程的第j个未知数的系数
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n+1;j++){
			cin>>a[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		int st=i;
		for(int j=i+1;j<=n;j++){
			if(a[j][i]>a[st][i]){//选取一个最大值减小误差
				st=j;
			}
		}
		for(int j=1;j<=n+1;j++){
			swap(a[i][j],a[st][j]);//i和st对换
		}
		if(a[i][i]==0){
			puts("No Solution");
			return 0;
		}
		for(int j=1;j<=n+1;j++){
			if(i!=j){
           //当前消到第i个未知数，那么当做到第j个方程时，其第i个未
           //知数的系数就是a[j][i]，那么这个方程就应该整体减去
           //a[j][i]/a[i][i]倍的方程i
				for(int k=i+1;k<=n+1;k++){//前面已经都是0了
					a[j][k]-=a[i][k]*a[j][i]/a[i][i];
				}
			}
		}
	}
	for(int i=1;i<=n;i++){
		printf("%.2lf\n",a[i][n+1]/a[i][i]);
	}
	
	return 0;
}

逻辑运算

eeeeeeee,学学玩的

1. 对于一个仅由\(\land\)或\(\lor\)(加不加\(!\))都一样是满足交换律的,枚举易证.

2. \(!(p \land q)=!p \lor !q\)

3. \(!(p \lor q)=!p \land !q\)

4. 韦恩图很厉害,能解决三个命题以下的问题