标签：密度估计 frac text 带宽 np 最优 hat

1.一维核密度

许多实际问题中，总体的分部类型事先并不知道。这就需要我们，首先根据实际情况对总体的分布类型提出某种假设，然后再根据样本提供的信息检验此假设是否合理。这种假设检验称为非参数假设检验或分布拟合检验.

• 皮尔逊卡方拟合检验法
• 偏度-峰度检验法
• 秩和检验
• 科尔莫哥洛夫检验

以上方法可以实现当个曲线的检验。当涉及多个曲线检验时

• 核密度估计(KDE)
  • 核密度估计(KDE)由Rosenblatt(1955)和Emanuel Parzen(1962)提出，又名Parzen窗(Parzen window)

2.核函数

设样本服从的分布概率函数为 \(F(x), x \in \mathbb{R}\) , 要求 \(F(x)\) 连续可导。当 \(n \rightarrow 0\) 时:

\[F(x)=P(X \leq x)=\frac{1}{n} \sum_{i=1}^n 1 \{x_i \leq x\} \]

概率密度函数 \(\hat{f}(x) = \frac{d F(x)}{d x} = \lim_{h \rightarrow 0^{+}} \frac{F(x+h) - F(x-h)}{2h}\) , 当 \(h\) 不大,且不小的时候:

\[\hat{f}(x) = \frac{F(x+h) - F(x-h)}{2h} = \frac{1}{nh} \sum_{i=1}^n 1 \{ \mid \frac{x-x_i}{h} \mid \leq 1\} \]

示性函数 \(1/2 \{\mid \frac{x-x_i}{h} \mid \leq 1\}\) 可以写为 \(K(\frac{x-x_i}{h})\) , 令 \(t = \frac{x-x_i}{h}\) , 称函数 \(K(t)\) 为核函数, \(\hat{f}(x)\) 为 \(f(x)\) 核密度估计.

对核函数 \(K(t)\) 作出如下规定:

1. \(K(t) \geq 0\)
2. \(K(-t) = K(t)\)
3. \(\int_{\text{R}}K(t) dt = 1\)
4. \(\int_{\text{R}}{t K(t) dt} = 0\)
5. \(\text{A}_{\alpha \beta} = \int_{\text{R}} t^{\alpha} \left [ K(t) \right ] ^{\beta} dt\) 都存在, 其中 \(\alpha = 0,1,2, \dots; \beta = 1,2,3, \dots\)

---

一维核密度估计 \(\hat{f}(x)\) 的性质, 其中 \(h\) 为核密度估计的带宽, \(n\) 为样本个数

1. 非负数 \(\hat{f}(x) \geq 0\)
2. \(\int_{\text{R}}\hat{f}(x) dx = 1\)
3. \(E(X) = \int_{\text{R}} x \hat{f}(x) dx = \overline{X}\) , 数学期望等于样本均值
4. \(D(X) = A_{12} h^2 + S_n^2\) , \(S^2_n\) 为二阶中心矩
5. \(\lim\limits_{h \rightarrow 0^+ \atop n \rightarrow +\infty } E[\hat{f}(x)] = f(x)\) 渐进无偏性

3.最优带宽的计算

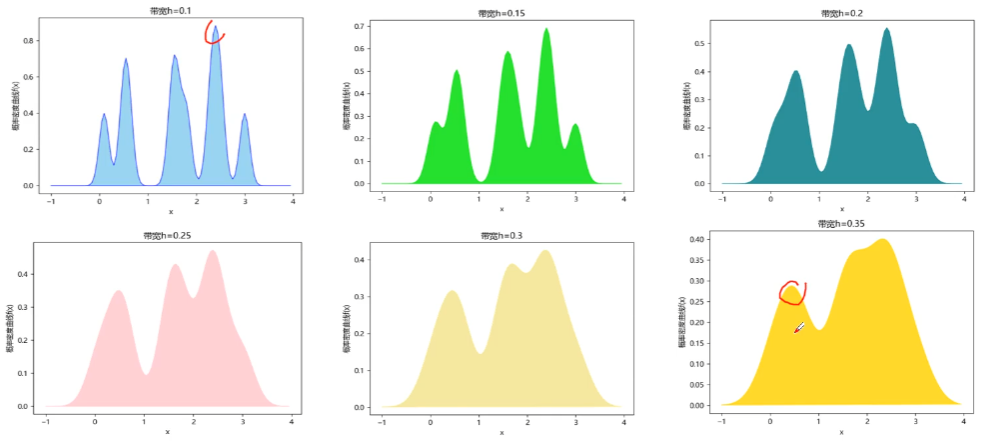
随着带宽的增加, 峰值逐渐变平缓, 峰的数量变少, 数据的方差越大. 因此需要一个方法, 衡量带宽选择的优劣.

• 迭代法
• 拇指法
• 交叉验证法

3.1 迭代法

第2步, 收敛慢!

3.2 拇指法

拇指法来源于 Silverman。若选用高斯核, 则最优带宽 \(h\) :

\[h = \hat{\sigma} \sqrt{\frac{4}{3n}}= \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}} \times \sqrt{\frac{4}{3n}} \]

3.3 交叉验证

适用于一维和二维

from sklearn.neighbors import KernelDensity
from sklearn.model selection import LeaveOneOut,GridSearchCV

bandwidth = np.linspace(0,10,100)
grid = GridSearchCV(KernelDensity(kernel='exponential'),{'bandwidth':bandwidth},cv=LeaveOneOut()))

grid.fit(A)#A中存放的是原始数据，可以是一维或二维

h_good = grid.best_params_.get('bandwidth')

3.4 具体应用

计算步骤

1. 计算最优带宽
   \(h = \hat{\sigma} \sqrt{4/{3n}}\)
2. 构造高斯核函数
3. 构造高斯核密度估计函数并绘制图像
4. 计算对应的均值和方差

import numpy as np
from sklearn.metrics import auc
import matplotlib.pyplot as plt
import matplotlib

#样本
X=[93,75,83,93,91,85,84,82,77,76,77,95,94,89,91,88,84,83,96,81,
  79,97,78,75,67,69,68,84,83,81,75,66,85,70,94,84,83,82,80,78,
  74,73,76,70,86,76,89,90,71,66,86,73,80,94,79,78,77,63,53,55]

#计算最优带宽
h=np.std(X,ddof=1)*(4/(3*len(X)))**0.2

#计算数学期望
print('E(X)='+str('%.2f'%np.mean(X)))

#定义高斯核函数
def K(x,xi):return 1/(2*np.pi)**0.5*np.exp(-((x-xi)/h)**2/2)

#计算方差
print('D(X)='+str('%.2f'%(h**2+np.var(X,ddof=0))))
'''
#定义余弦核函数
def k(x,xi):
   if b-h<=a<=b+h:return np.pi/4*np.cos(np.pi/2*((x-xi)/h))
   else:return 0
#计算方差
print('D(X)='+str('%.2f'%((1-8/np.pi**2)*h**2+np.var(X,ddof=0))))
#定义均匀核函数
def k(x,xi):
   if xi-h<=x<=xi+h:return 0.5
   else:return 0
#计算方差
print('D(X)='+str('%.2f'%(h**2/3+np.var(X,ddof=0))))
'''

#定义高斯核密度估计函数
def f(x):return sum(K(x,xi) for xi in X)/(len(X)*h)

#计算样本属于区间[a,b]概率
def P(a,b):
  x=np.arange(a,b,0.01)
  y=[f(i) for i in x]
  return auc(x,y)
print('P(80≤X≤100)='+str('%.3f'%P(80,100)))

#绘制高斯核密度估计函数的图像
x=np.arange(40,120,0.1)
y=[f(i) for i in x]
plt.title('h='+str('%.3f'%h))
plt.fill(x,y,facecolor='green',alpha=0.5)
plt.plot(x,y,'r-')
plt.xlabel('x')
plt.ylabel('核密度估计函数f(x)')
plt.show() 

标签：密度估计,frac,text,带宽,np,最优,hat
From： https://www.cnblogs.com/AidanLee/p/18031032