Abstract
我们提出了一种非常简单的图对比学习方法作为推荐,该方法放弃了无效的图增强,而是使用一种简单而有效的基于噪声的嵌入增强来生成CL的视图
Introduction
这里介绍以下SimGCL的缺点:
除了推荐任务的正向/反向传递外,每个小批内的对比任务还需要两个额外的正向和反向传递,也就是计算成本很大,所以之后重点要解决的就是计算成本问题
为了解决这个问题,本研究提出了一种非常简单的图对比学习方法作为推荐。XSimGCL建立在SimGCL的基于噪声的增强方法之上,同时通过一个统一推荐和对比任务的共享单通道来简化计算过程。不同之常在于,SimGCL对比了通过不同的正向传递学习到的两个最终表示,并依赖普通表示进行推荐,而XSimGCL对两个任务使用相同的扰动表示,并用跨层对比替换了SimGCL中的最后一层对比
两种方法的对比图如下:
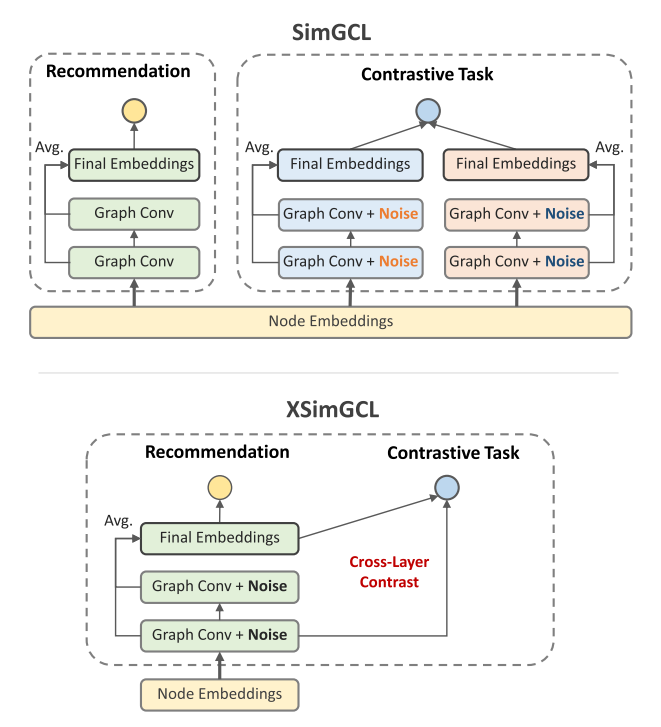
我们的工作有以下贡献:
- 我们阐明了对比学习对图推荐模型的有益影响,特别是通过学习更均匀分布的表示,其中InfoNCE损失比图增强的意义更大
- 我们提出了一种简单而有效的基于噪声的增强方法,它可以平滑地调整学习表示的均匀性
- 我们提出了一种新的基于CL的推荐模型,XSimGCL,它在有效性和效率方面都超过了SimGCL。此外我们还进行了理论分析来解释XSimGCL的优越性
Method
虽然在基于CL的推荐系统中将推荐任务和对比任务的管道分开似乎是一种惯例,但我们质疑这种体系结构的必要性
在使用CL时,有一个最佳点,即相关视图之间的互信息既不是过高也不是过低,然而在SimGCL中,同一节点的一对视图之间的互信息可能总是非常高的,为了解决这个问题,我们对比不同的图层嵌入。这些嵌入具有一些共同的信息,但在聚合的邻居和添加的噪声上有所不同,这符合最优点理论。,此外由于添加的噪声大小很小,可以直接使用扰动表示来进行推荐,不过只在训练时使用扰动表示,测试的时候还是使用普通模式
受益于这种设计,我们可以通过合并SimGCL的编码过程来简化其体系结构。这推导出了一个新的体系结构,它在小批量计算中只有一次前向和反向传递。
XSimGCL的损失函数为:
\(\begin{aligned}\mathcal{L}&=-\sum_{(u,i)\in\mathcal{B}}\log\left(\sigma(\mathbf{e}_u^{\prime\top}\mathbf{e}_i^{\prime}-\mathbf{e}_u^{\prime\top}\mathbf{e}_j^{\prime})\right)\\\\&+\lambda\sum_{i\in\mathcal{B}}-\log\frac{\exp(\mathbf{z}_i^{\prime\top}\mathbf{z}_i^{l^*}/\tau)}{\sum_{j\in\mathcal{B}}\exp(\mathbf{z}_i^{\prime\top}\mathbf{z}_j^{l^*}/\tau)}\end{aligned}\)
\(l^{*}\)表示要与最后一层对比的那一层,选择最后一层的原因是最后一层会导致最佳的性能