多项式
若 \(A(x)=a_0+a_1x+a_2x^2+ \dots a_nx^n(a_n \ne 0)\),则称 \(A\) 是 \(n\) 次多项式。
初中概念,但在 OI 中可以玩出花来。
多项式的表示方式
像上面的介绍一样,用系数 \(a_0,a_1, \dots a_n\) 来表示多项式的方法称为系数表示法。
还有一种表示多项式的方法,就是对于 \(n\) 次多项式,给出 \(n+1\) 对点,\((x_0,A(x_0)),(x_1,A(x_1)),(x_2,A(x_2)) \dots (x_n,A(x_n))\), 且 \(x_0,x_1 \dots x_n\) 互异,称为 点值表示法。
可以证明,点值表示法和系数表示法一一对应,表示唯一的多项式。
系数表示法 \(\rightarrow\) 点值表示法:带入计算即可,复杂度 \(O(n^2)\)。
点值表示法 \(\rightarrow\) 系数表示法:需要使用拉格朗日插值,复杂度 \(O(n^2)\)。
之后我们引入 FFT,可以实现 \(O(n \log n)\) 时间内两种表示法的转化。
多项式乘法
多项式乘法是多项式的核心操作。
若有两个多项式 \(A(x) = \sum_{i=0}^na_ix^i\),\(B(x) = \sum_{i=0}^mb_ix^i\),其乘积为
\[M(x)=A(x)B(x)=\sum_{i=0}^{n}\sum_{j=0}^{m}a_ib_jx^{i+j} \]就是简单的代数运算,\(n\) 次多项式和 \(m\) 次多项式的乘积次数是 \(n+m\)。
直接硬乘复杂度自然是 \(O(n^2)\)。
对于点值表示法,两个多项式预先准备 \(n+m+1\) 对点,然后乘起来,得 \((x_{ai}x_{bi},A(x_{ai})B(x_{b_i}))\)。
这 \(n+m+1\) 对点足够表示出多项式。 复杂度是 \(O(n)\)。
可以看出,点值表示法做乘法速度很快,但系数表示法无论是直接乘还是转化为点值乘,都是 \(O(n^2)\),为了解决这个问题,就要请出 FFT——快速傅里叶变换了。
FFT
简介
我们如果将 \(n+1\) 个普通的数带入多项式计算点值,复杂度难以优化。而 FFT,简单来说,就是通过带入特殊的数,来加速系数表示 \(\rightarrow\) 点值表示的速度。
单位复数根
基础知识:数学必修二(其实就是复数)
在复数域内,对于方程 \(w^n=1\),一共有 \(n\) 个解,由
\[e^{iu}=\cos u+i \sin u \]可得,为 \(e^{2 \pi ik/n}\),其中 \(k=0,1\dots n-1\),称为 \(n\) 次单位复数根。
对于 \(k=1\),我们定义其为 \(w_n=e^{2\pi i/n}\),称为主 \(n\) 次单位复数根。那么这 \(n\) 个根就可以表示为 \(w_n^0,w_n^1 \dots w_n^{n-1}\),它们均匀分布在复平面单位圆上。
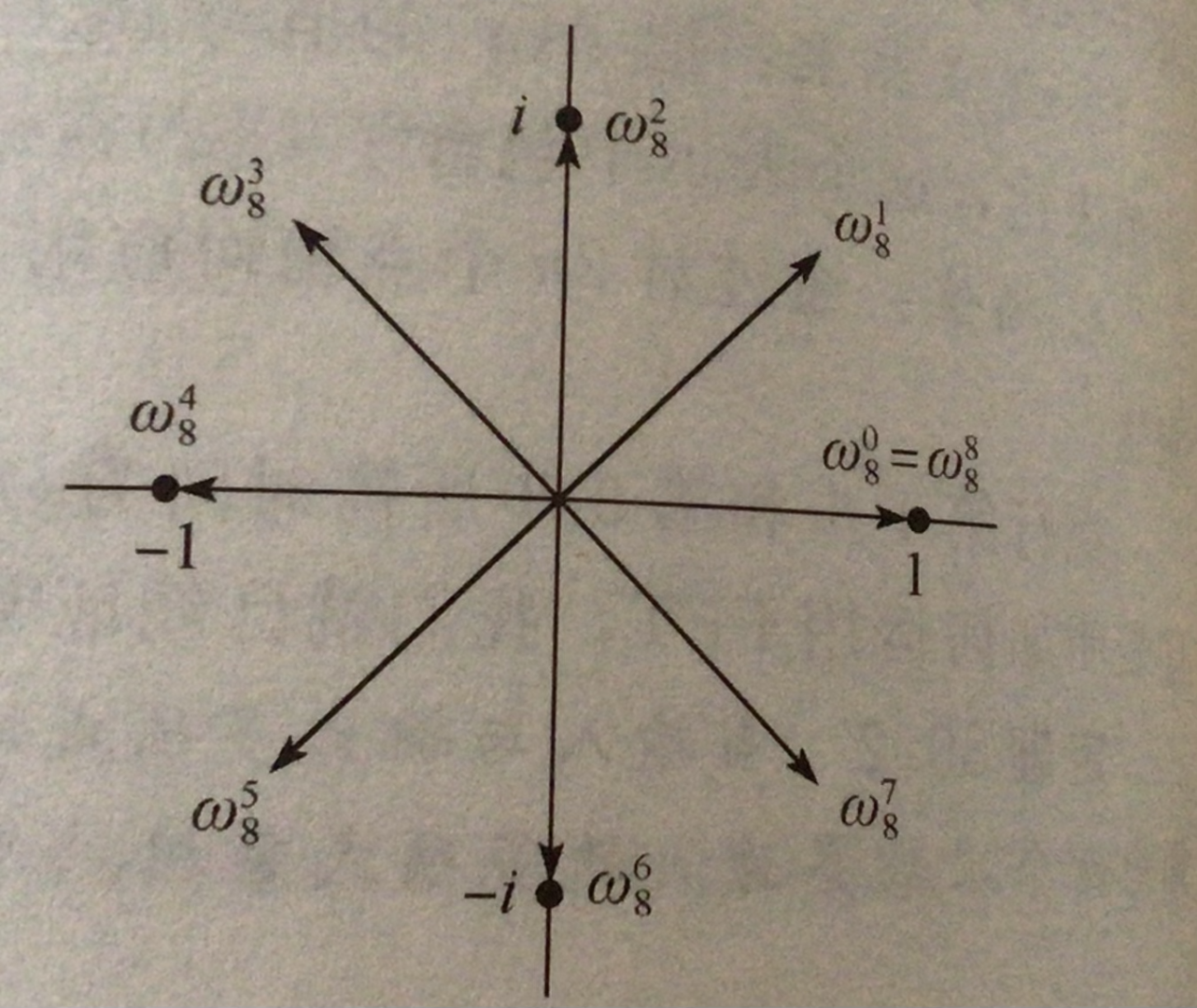
性质一
\(w_{dn}^{dk}=w_{n}^{k}\)(因为单位复数根是在单位圆上均分,所以只看比例 \(k/n\))
引理
若 \(n\)为偶数,\((w_n^k)^2=w^k_{n/2}\)
性质二
若 \(n\) 为偶数,\(w_n^k=-w_n^{k+n/2}\)(几何解释:转半圈)
快速傅里叶变换
利用单位复数根的性质,我们通过分治法代入 \(n\) 次单位复数根,来得到 \(n-1\) 次多项式的点值表示。
基于这样一个分治思想,令 \(A^{[0]}(x) = a_0+a_2x+a_4x^2\dots\),\(A^{[1]}(x)=a_1+a_3x+a_5x^2\dots\),就是把偶数项系数和奇数项系数分给两个多项式,那么就有
\[A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2) \]对 \(A^{[0]}(x),A^{[0]}(x)\) 分治计算即可。
这样并不能优化复杂度,因为普通的值代入多项式,\(A^{[0]},A^{[1]}\) 实际要计算 \(x_1, x_2^2,x_3^2\dots\) 共 \(n\) 个值,但又有它们是 \(n/2\) 次多项式,理论上只需要代入 \(n/2\) 个值。
这个时候,单位复数根就起作用了,如果计算 \(A(w_n^k)\),分治时,\((w_n^k)^2\) 变为了 \(w_{n/2}^k\),就有
\[A(w_n^k)=A^{[0]}(w_{n/2}^k)+w_n^kA^{[1]}(w_{n/2}^k) \]同时根据性质二,有
\[A(w_n^{k+n/2})=A^{[0]}(w_{n/2}^k)-w_n^kA^{[1]}(w_{n/2}^k) \]那么对于 \(A^{[0]},A^{[1]}\),它们只要计算 \(n/2\) 个值就行了,复杂度为 \(T(n)=2T(n/2)+n\),为 \(O(n \log n)\)。
边界是 \(n=1\) 的情况,此时 \(A(w_1^0)=A(1)=a_0\)
下面是 FFT 的递归模版,将系数表示原址转化为点值表示
void FTT(complex<double>* A, int n) {
if (n == 1) return ; // A(w_1^0)=A(1)=a_0
vector<complex<double>> tmp(n);
complex<double> wn(cos(2 * pi / n), sin(2 * pi / n)); //n次单位复数根计算
complex<double> wk(1, 0);
for (int i = 0; i < n; i++) {
if (i & 1) tmp[i / 2 + n / 2] = A[i];
else tmp[i / 2] = A[i];
}
for (int i = 0; i < n; i++) A[i] = tmp[i];
// 对A数组进行原址划分,递归左右两部分
// 得出来的A数组[0,n/2)内储存A0(w_n/2)
// [n/2,n)内储存A1(w_n/2)
vector<complex<double>>().swap(tmp);
FTT(A, n / 2), FTT(A, n / 2);
for (int i = 0; i < n / 2; i++, wk *= wn) {
auto x = A[i], y = A[i + n / 2];
A[i] = x + wk * y;
A[i + n / 2] = x - wk * y;
}
}
在 FFT 过程中,要确保 \(n\) 随时为偶数,所以最初 \(n\) 必须得是 \(2\) 的幂。
这里使用了 c++ 的复数模版进行运算,如果只在理论层面上学习 FFT,已经可以完结撒花了。但是,这个模版有几个缺陷。
1.使用复数运算,递归,且多次复制数组,造成了时间空间的巨大开销/
解决方案:自定义复数运算,学习接下来的FFT的迭代实现。
2.三角函数带来的精度问题
解决方案:我们之后介绍的快速数论变换会解决整数多项式在精度上的问题。
FFT 的迭代实现
为了优化常数,我们要将递归改为循环迭代,这是个很考验 FFT 原理的活。
首先递归FFT中有“划分奇偶系数”这一操作,观察递归树。
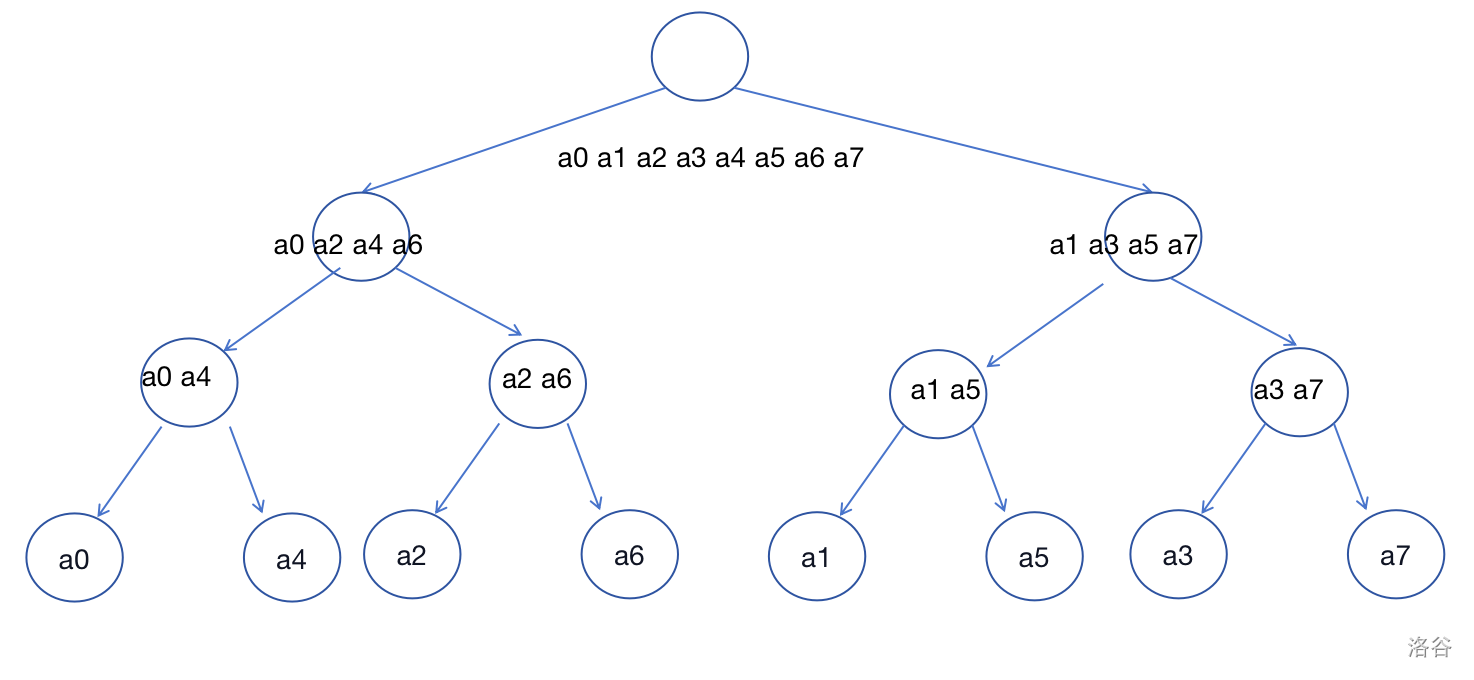
原来的 \(a_0,a_1\dots a_8\) 变为了 \(a_0,a_4,a_2,a_6,a_1,a_5,a_3,a_7\),如果细心的话,可以发现最后 \(a_i\) 所在的下标就是
\(i\) 二进制倒过来,举两个例子
\(a_3:011 \rightarrow 110; 3\rightarrow 7\)
\(a_4:100 \rightarrow 001; 4\rightarrow 1\)
证明很简单,第 \(k\) 层划分是看 \(i\) 第 \(k\) 位是否为 \(1\),然后以 \(2^{dep-k}\) 的权值加到新下标上,所以就是二进制倒过来啦。
我们可以 \(O(n)\) 递推求解 \(0\dots n-1\) 内的倒二进制。
for (int i = 0; i < n; i++) { //自行模拟
rev[i] = rev[i >> 1] >> 1;
if (i & 1) rev[i] |= n >> 1;
}
这被称为 位逆序置换。
“划分”完了,我们要考虑“合并”,这个和递归的合并并无二异,当前 \(A^{[0]}(x)\) 和 \(A^{[1]}(x)\) 分别记录在 \([0,n/2)\) 和 \([n/2,n)\) 中。调用然后覆盖即可。
下面给出代码
//已经计算好 rev
void FFT(auto *A, int n) {
for (int i = 0; i < n; i++) {
if (i < rev[i]) swap(A[i], A[rev[i]]);
}
for (int i = 1; i < n; i <<= 1) { //这里i是枚举 n/2,
auto wn = ...
for (int j = 0; j < len; j += (i << 1)) { //处理[j,j+n)
auto wk(1, 0)...
for (int k = 0; k < i; k++, wk = wk * wn ) {
auto x = A[j + k], y = A[i + j + k];
A[j + k] = x + wk * y;
A[i + j + k] = x - wk * y;
}
}
}
}
逆变换——IDFT
我们由上文知道了系数转点值,那么点值怎么转系数呢?
注意,这里的点值应是通过 FFT 转换过来的 \(A(w_n^k)\),
直接看结论:对点值数组以 \(w_n^{-k}\) 为单位复数根,进行一次 FFT,然后每一个数除以 \(n\)。
我们直接把单位复数根判断写进 FFT 里,就能 FFT IDFT 一起了。
证明:
有 \(A(w_n^k)=a_0+a_1w_n^k+a_2w_n^{2k}+\dots\)
\(A(w_n^k)w_n^{-ki}=a_0w_n^{-ki}+a_1w_n^{k(1-i)}+a_2w_n^{k(2-i)}+\dots\)
我们对 \(k\) 求和:
\(\displaystyle\sum_{k=0}^{n-1}{A(w_n^k)w_n^{-ki}}=a_0(w_n^0+w_n^{-i}+w_n^{-2i}+\dots)+a_1(w_n^0+w_n^{1-i}+w_n^{2(1-i)}+\dots)+\dots\)
由等比数列求和公式,可得:
\(w_n^{0k}+w_n^{1k}+\dots w_n^{(n-1)k}=\displaystyle\frac{w_n^{nk}-w_n^0}{w_n^k-1}=0\)
所以对于第 \(i\) 项 \(w_n^{-i}\),将其代入多项式 \(F(x)=A(w_n^0)+A(w_n^1)x+A(w_n^2)x^2+\dots\) 中,非 \(i\) 项全部被消掉,只留下 \(na_i\),所以就是这样了。
快速数论变换——NTT
这个其实可以单讲的,但其实原理和 FFT 一模一样,只不过把单位复数根换成了原根。对于整数多项式,消除了误差。
前置知识:原根(这玩意真的很有用啊)
我们使用单位复数根是因为它很好的性质,平方后数量减半,我们用原根也能达到这样的效果。由于简便,下面的等号都是在模意义上相等。
选取一个奇素数 \(p\),然后找到原根 \(g\),
我们令 \(n\) 次主单位根 \(w_n=g^{(p - 1)/n}\),可以发现 \(w_n^n=g^{p-1}=1=w_n^{0}\),形成了一个环。
然后对于性质一,自然成立;
对于性质二,\(w_n^{n/2}= g^{(p-1)/2}=-1\),所以成立。
那么和 FFT 代码基本一样,只不过把复数换成了模运算。
由于 \(n\) 要整除 \(p-1\),还得是 \(2\) 的幂,我们尽可能让 \(p-1\) 有较多的 \(2\),可以选取 \(998244353=2^{23}*119+1\)。
最终模版(我还是觉得NTT好用)
const int N = 1 << 22;
const int mod = 998244353, g = 3;
const int gi = pow_mod(3, mod - 2);
void init() {
for (int i = 0; i < len; i++) {
rev[i] = rev[i >> 1] >> 1;
if (i & 1) rev[i] |= len >> 1;
}
}
void NTT(int *A, int len, bool t) {
for (int i = 0; i < len; i++) {
if (i < rev[i]) swap(A[i], A[rev[i]]);
}
for (int i = 1; i < len; i <<= 1) {
int wn = pow_mod(t ? g : gi, (mod - 1) / (i << 1));
for (int j = 0; j < len; j += (i << 1)) {
int w0 = 1;
for (int k = 0; k < i; k++, w0 = w0 * wn % mod) {
int x = A[j + k], y = w0 * A[i + j + k] % mod;
A[j + k] = (x + y) % mod;
A[i + j + k] = (x - y + mod) % mod;
}
}
}
if (!t) {
int inv = pow_mod(len, mod - 2);
for (int i = 0; i < len; i++) A[i] = A[i] * inv % mod;
}
}