2.基础查找
所谓查找,就是在查找空间中找寻符合要求的解的过程。查找方法有多种,下面简单介绍3种。不同的策略对查找的效率和结果有不同的影响。
2.1 线性查找
从首元素开始,遍历整个序列,直到找到目标元素,则结束算法;或者遍历完序列还没有匹配,则查找失败结束算法。时间复杂度为O(n)。

线性查找
//基础查找-线性查找 2024-02-15
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 100 + 10;
int arr[MAXN];
//线性查找
bool LinearSearch(int n, int target)
{
for(int i=0; i<n; i++)
{
if(target == arr[i])
return true;
}
return false;
}
int main()
{
int n;
scanf("%d", &n);
for(int i=0; i<n; i++)
{
scanf("%d", &arr[i]);
}
int m, target;
scanf("%d", &m);
for(int i=0; i<m; i++)
{
scanf("%d", &target);
if(LinearSearch(n, target))
{
printf("YES\n");
}
else{
printf("NO\n");
}
}
return 0;
}
2.2 二分查找
二分查找的前提是有序序列。有两种方法,一种是自定义,自己写一个函数用来贴合题面的要求;第二种是内定义,即使用C++内部封装好的函数来实现二分查找。时间复杂度为O(logn)。
2.2.1 自定义
定义两个变量L和R分别指向首元素和序列的尾元素,计算middle,如果middle所指向的元素和要找的目标值target相等,则查找成功,结束算法;否则如果middle所指向的元素比target小,则在右半边继续查找;左半边同理;直至查找到目标值,或者当R<L时算法结束,查找失败。
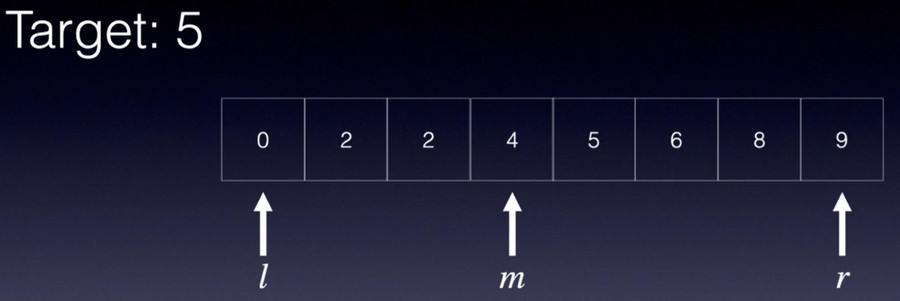
二分查找_自定义
//基础查找-二分查找-前提序列有序-自定义 2024-02-15
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 100 + 10;
int arr[MAXN];
bool BinarySearch(int n, int target)
{
int left = 0;
int right = n-1;
while(left <= right)
{
int middle = left + (right - left)/2;
if(arr[middle] == target)
{
return true;
}
else if(arr[middle] < target)//搜索右半部分
{
left = middle + 1;
}
else{
right = middle -1;
}
}
return false;
}
int main()
{
int n;
scanf("%d", &n);
for(int i=0; i<n; i++)
{
scanf("%d", &arr[i]);
}
sort(arr, arr+n);//默认compare升序
int m, target;
scanf("%d", &m);
for(int i=0; i<m; i++)
{
scanf("%d", &target);
if(BinarySearch(n, target))
{
printf("YES\n");
}
else{
printf("NO\n");
}
}
return 0;
}
2.2.2 内定义
C++内部封装了两个用于实现二分查找的函数,即lower_bound和upper_bound。需要引用头文件#include <algorithm>
1、lower_bound:返回大于或等于目标值的第一个位置。
2、upper_bound:返回大于目标值的第一个位置。
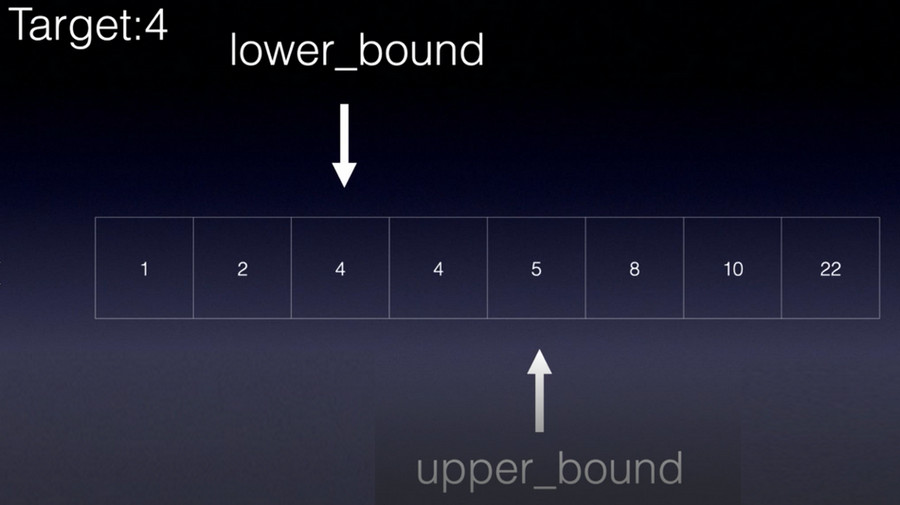
lower_bound(first, last, target)有三个参数,分别是有序序列的起始地址、结束地址和目标值,target可为任意数据类型。
注意考虑lower_bound在查找目标值时的3种情况。其一如上图所示;其二是有序序列中没有目标值,lower_bound会返回最靠近目标值而大于目标值的元素的下标;其三,要查找的target值大于有序序列的最大值,此时lower_bound会移出序列,指向下标n,即越界访问。
注意:lower_bound函数返回的不是数组元素的下标,而是元素所在的地址,减去数组起始地址,即可得到数组下标。int position = lower_bound(arr, arr+n, target) - arr;
二分查找_内定义
//基础查找-二分查找-前提序列有序-内定义 2024-02-15
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 100 + 10;
int arr[MAXN];
int main()
{
int n;
scanf("%d", &n);
for(int i=0; i<n; i++)
{
scanf("%d", &arr[i]);
}
sort(arr, arr+n);//默认compare升序
int m, target;
scanf("%d", &m);
for(int i=0; i<m; i++)
{
scanf("%d", &target);
int position = lower_bound(arr, arr + n, target) - arr ;
if(position != n && arr[position] == target)
{
printf("YES\n");
}
else{
printf("NO\n");
}
}
return 0;
}
2.3 散列查找
线性查找和二分查找都是以数组下标为索引,去遍历查找target值,而散列查找使用散列函数,使得元素值经过常数时间的Hash函数计算后,直接得到其下标索引。时间复杂度为O(1)。
散列查找也有两种方法,一种是自定义,一种是内定义。

2.3.1 自定义
这里散列函数搞一个最简单的线性映射,即开一个和数据范围一样大的bool型辅助数组,在输入元素时,给对应的辅助数组赋值为true。未得到赋值的默认为false。
散列查找_自定义
//基础查找-散列查找 2024-02-15
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 100 + 10;
const int RANGE = 1e6;
int arr[MAXN];
bool hashTable[RANGE];
int main()
{
int n;
scanf("%d", &n);
for(int i=0; i<n; i++)
{
scanf("%d", &arr[i]);
hashTable[arr[i]] = true;
}
sort(arr, arr+n);//默认compare升序
int m, target;
scanf("%d", &m);
for(int i=0; i<m; i++)
{
scanf("%d", &target);
if(hashTable[target])
{
printf("YES\n");
}
else{
printf("NO\n");
}
}
return 0;
}
2.3.2 内定义
C++内部封装了散列函数unordered_map,需要引用头文件#include <unordered_map>。
散列查找_内定义
//基础查找-散列查找-内定义 2024-02-15
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int MAXN = 100 + 10;
int arr[MAXN];
unordered_map<int, bool> hashTable;//1:元素的类型;2:是否出现过用bool表示
//相当于定义了一个辅助数组用于线性映射,就是散列函数
int main()
{
int n;
scanf("%d", &n);
for(int i=0; i<n; i++)
{
scanf("%d", &arr[i]);
hashTable[arr[i]] = true;
}
sort(arr, arr+n);//默认compare升序
int m, target;
scanf("%d", &m);
for(int i=0; i<m; i++)
{
scanf("%d", &target);
if(hashTable[target])
{
printf("YES\n");
}
else{
printf("NO\n");
}
}
return 0;
}
3.参考资料
1.C++ upper_bound()函数
2.rgb颜色对照表