[NOIP2002 普及组] 过河卒
题目描述
棋盘上 \(A\) 点有一个过河卒,需要走到目标 \(B\) 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 \(C\) 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,\(A\) 点 \((0, 0)\)、\(B\) 点 \((n, m)\),同样马的位置坐标是需要给出的。
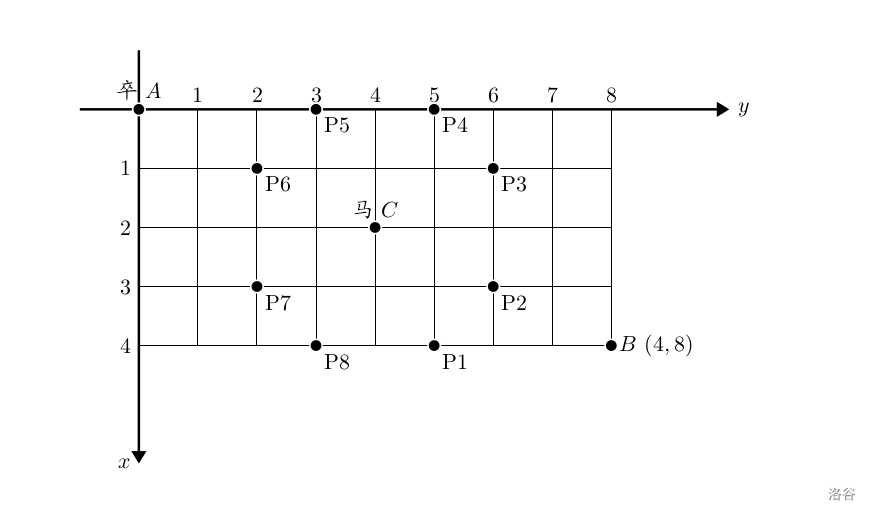
现在要求你计算出卒从 \(A\) 点能够到达 \(B\) 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 \(B\) 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
样例 #1
样例输入 #1
6 6 3 3
样例输出 #1
6
提示
对于 \(100 \%\) 的数据,\(1 \le n, m \le 20\),\(0 \le\) 马的坐标 \(\le 20\)。
【题目来源】
NOIP 2002 普及组第四题
题目分析
\(upd:\)迁移至博客园地址
马走日,象走田,卒子一去不复返
对于本题,卒子一开始的坐标为\((0, 0)\)
而对于卒子,所有格子的状态无非2种: 能走与不能走(1或者0)
但是我们还需要令起点从(0, 0)到(1, 1),即向右下方偏移一位
设dp[i][j]为从1到i的路径条数,我们可以得到对状态进行转移的方程:
\(dp[i][j] = dp[i - 1][j] + dp[i][j - 1]\)
long long dp[25][25];//别忘了定义
但是我们需要先给定格子状态再偏移
所以我们可以bitset一个mp[25][25]用来存储每个格子的状态
(开大些没坏处)
bitset<25> mp[N];
那么什么格子不能走呢?
马能走的格子啊(废话)
所以dp[马的x - 1][马的y + 2] = 0
dp[马的x - 1][马的y - 2] = 0
dp[马的x - 1][马的y + 2] = 0
dp[马的x + 1][马的y - 2] = 0
dp[马的x + 1][马的y + 2] = 0
dp[马的x - 2][马的y + 1] = 0
dp[马的x - 2][马的y + 1] = 0
dp[马的x + 2][马的y + 1] = 0
dp[马的x + 2][马的y + 1] = 0
如果觉得这些代码过于冗杂,可以两个数组 dx[8], dy[8]
代码如下:
int dx[8] = {1, 1, -1, -1, 2, 2, -2, -2};
int dy[8] = {2, -2, 2, -2, 1, -1, 1, -1};
//数组的元素必须一一对应
然后使用for循环处理mp
代码:
for(int i = 0; i < 8; i++)
{
int nx = x + dx[i], ny = y + dy[i];//x为马的坐标x,y为马的坐标y`
if(1 <= nx && nx <= n && 1 <= ny && ny <= m)
{
mp[nx][ny] = ture;//mp为一个二进制数组,相当于bool数组,其中的值表示能不能走
}
}
接下来就是偏移了
这个时候:这个\(dp[i][j] = dp[i - 1][j] + dp[i][j - 1]\)就派上用场了
dp[1][1] = 1;//别忘了将第一个格子初始化
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
if(i == 1 && j == 1) coutinue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
if(mp[i][j])dp[i][j] = 0;//如果走到马的控制点路径为0
}
}
最后输出dp[n][m]
cout << dp[n][m] << '\n';
完整AC代码:
#include <bits/stdc++.h>
using namespace std;
long long dp[25][25] = {0};
bitset<25> mp[25];
int dx[8] = {1, 1, -1, -1, 2, 2, -2, -2};
int dy[8] = {2, -2, 2, -2, 1, -1, 1, -1};
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, m, x, y;cin >> n >> m >> x >> y;
n++, m++, x++, y++;
mp[x][y] = true;
for(int i = 0; i < 8; i++)
{
int nx = x + dx[i], ny = y + dy[i];
if(1 <= nx && nx <= n && 1 <= ny && ny <= m)mp[nx][ny] = true;
}
dp[1][1] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
if(i == 1 && j == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
if(mp[i][j])dp[i][j] = 0;
}
}
cout << dp[n][m] << endl;
return 0;
}