首页 > 其他分享 >【LGR-172-Div.4】洛谷入门赛 #19 题解

【LGR-172-Div.4】洛谷入门赛 #19 题解

时间：2024-01-19 21:23:41浏览次数：30  
标签：10 洛谷 leq 19 题解 样例 int 输出 饼干

比赛链接：\(link\)

T1 分饼干 I

题目描述

洛谷网校举行了期末考试，同学们经过课程的学习，考出了优异的成绩。

Z 在考试中获得了第一名，yz 在考试中获得了第二名，老师决定买一些饼干奖励两名小朋友。

老师买了三盒饼干，第一盒有 \(a\) 块饼干，第二盒有 \(b\) 块饼干，第三盒有 \(c\) 块饼干。老师决定将这三盒饼干奖励给 Z 和 yz，三盒饼干不可以被拆开奖励。

老师希望 Z 拿到的饼干块数不少于 yz，但又希望两人拿到的饼干数量差距尽可能小，请问 Z 和 yz 各拿到几块饼干？

输入格式

输入一行三个整数，分别为 \(a,b,c\)。

输出格式

输出一行两个整数，由空格分隔。第一个整数代表 Z 拿到的饼干数量，第二个整数代表 yz 拿到的饼干数量。

样例 #1

样例输入 #1

3 1 5

样例输出 #1

5 4

样例 #2

样例输入 #2

3 3 5

样例输出 #2

6 5

提示

样例解释 1

Z 拿走 \(5\) 块饼干，yz 拿走 \(3+1=4\) 块饼干。

样例解释 2

Z 拿走 \(3+3=6\) 块饼干，yz 拿走 \(5\) 块饼干。

思路

由题意可知，分配给两人的饼干必定是一人一盒，另一人两盒。

所以暴力求解，列出三种情况。其中拿到两盒饼干的人分别可能是\(a+b,a+c,b+c\)。于是分别求解即可。

代码实现

#include<bits/stdc++.h>
using namespace std;
int main()
{
	ios::sync_with_stdio(false);
	int a,b,c;
	cin>>a>>b>>c;
	int _[3]={a+b,a+c,b+c};
	int _1=abs(_[0]-c);
	int _2=abs(_[1]-b);
	int _3=abs(_[2]-a);
	int mn=min(_1,min(_2,_3));
	if(mn==_1)
	{
		cout<<max(_[0],c)<<" "<<min(_[0],c)<<endl;
	}
	else if(mn==_2)
	{
		cout<<max(_[1],b)<<" "<<min(_[1],b)<<endl;
	}
	else if(mn==_3)
	{
		cout<<max(_[2],a)<<" "<<min(_[2],a)<<endl;
	}
	return 0;
}

T2 分饼干 II

题目描述

老师有 \(N\) 块饼干，要分给 \(k\) 名小朋友。

每名小朋友至少拿到一块饼干，老师想让每名小朋友拿到的饼干数量都不一样多，请问老师能否实现这个目标。

输入格式

本题单个测试点内有多组测试数据。

输入共 \(T + 1\) 行。

输入第一行为一个整数 \(T\)，代表测试数据组数。
接下来 \(T\) 行，每行两个整数，分别为 \(N,k\)。

输出格式

输出共 \(T\) 行，依次对应 \(T\) 组测试数据。如果该组测试数据

  • 可以实现，输出 Yes。
  • 无法实现，输出 No。

样例 #1

样例输入 #1

1
1 1

样例输出 #1

Yes

样例 #2

样例输入 #2

1
5 3

样例输出 #2

No

提示

数据规模与约定

  • 对于 \(50\%\) 的测试数据 \(1 \le k \le 1000\)，\(1 \le N \le 10^6\)。
  • 对于 \(100\%\) 的测试数据，\(1 \le k,N \le 10^9\)。

思路

设想一个长度为\(k\)的序列，由\(1~k\)构成，和为\(n\)，这正好是一个符合题意的饼干分配方式。

于是转化成数学，将\(n\)循环减去\(1~k\)。若最后\(n\)没有被正好减成\(0\)，说明该序列不存在。

代码实现

#include<bits/stdc++.h>
using namespace std;
int main()
{
	ios::sync_with_stdio(false);
	int t;
	cin>>t;
	while(t--)
	{
		int n,k;
		cin>>n>>k;
		int j=1,flag=1;
		do{
			n-=j;
			if(n<0)
			{
				cout<<"No"<<endl;
				flag=0;
				break; 
			}
			j++;
		}while(j<=k);
		if(flag==1) cout<<"Yes"<<endl;
	}
	return 0;
}

T3 跳房子

题目背景

跳房子，也叫跳飞机，是一种世界性的儿童游戏，也是中国民间传统的体育游戏之一，趣味性、娱乐性极强，曾深受广大儿童的喜爱。

题目描述

现在我们给出一种简易跳房子游戏的玩法：

\(n\) 个格子从左到右一字形排开，从左到右依次被标号为 \(1, 2, \cdots, n\)。每一个格子上都有一个正整数，\(i\) 号格子上的正整数是 \(a _ i\)。

这个游戏的规则如下：初始时玩家站在 \(1\) 号格子上，需要做若干次跳跃。每一次跳跃时，玩家需要从当前格子向前跳「当前格子上写的整数」数量的格子。形式化地讲，如果玩家当前处于 \(x\) 号格子，玩家需要跳到 \(x + a _ x\) 号格子上。

如果玩家跳到 \(n\) 号格子右侧的位置，称玩家出界；如果玩家恰好跳到 \(n\) 号格子上，称玩家胜利。这两种情况下玩家都需要停止跳跃。

现在给定格子数量和格子上的整数，你需要求解：

  1. 在停止跳跃后，玩家是否胜利。即，玩家是否能够恰好跳到 \(n\) 号格子上。
  2. 在停止跳跃后，玩家跳跃的总次数。

输入格式

输入共两行。

第一行为一个整数 \(n\)，代表格子的数量。
第二行为 \(n\) 个整数 \(a _ 1, a _ 2, \cdots, a _ n\)，代表每个格子上的数字。

输出格式

输出共两行。

第一行为一个字符串。如果玩家在停止跳跃后恰好跳到 \(n\) 号格子上，输出 Yes，否则输出 No。
第二行一个整数，代表玩家的总跳跃次数。

样例 #1

样例输入 #1

6
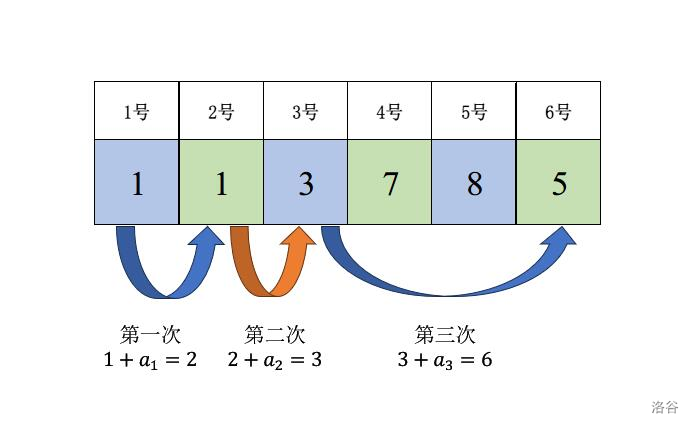
1 1 3 7 8 5

样例输出 #1

Yes
3

样例 #2

样例输入 #2

4
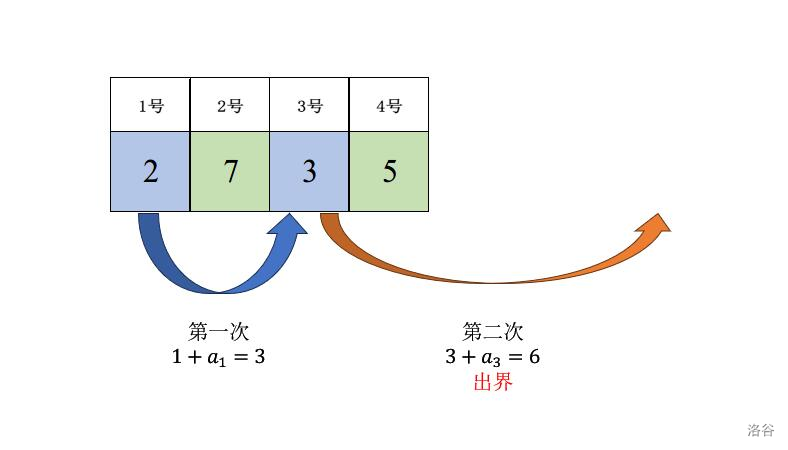
2 7 3 5

样例输出 #2

No
2

提示

样例 1 解释

样例 2 解释

数据规模与约定

对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 10 ^ 6\)，\(1 \leq a _ i \leq 10 ^ 4\)。

测试点编号 \(n\) 特殊性质
\(1\) \(= 1\) 无
\(2 \sim 4\) \(\leq 100\) 无
\(5\) \(\leq 10 ^ 6\) \(a _ i = 1\)
\(6, 7\) \(\leq 10 ^ 6\) \(a _ i = 2\)
\(8 \sim 10\) \(\leq 10 ^ 6\) 无

思路

由题意，模拟。

代码实现

#include<bits/stdc++.h>
using namespace std;
int a[1000005];
int main()
{
	ios::sync_with_stdio(false);
	int n;
	cin>>n;
	int i;
	for(i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	i=1;
	int ans=0;
	bool flag=0;
	while(i<=n)
	{
		if(i==n)
		{
			flag=1;
			break;
		}
		i+=a[i];
		ans++;
	}
	if(flag)
	{
		cout<<"Yes"<<endl<<ans<<endl;
	}
	else if(!flag)
	{
		cout<<"No"<<endl<<ans<<endl;
	}
	return 0;
}

T4 区间函数最小值

题目描述

给定 \(A, B, C, D, E, F, G, P, X_1, X_2, Y_1, Y_2\)，求当 \(X _ 1 \leq x \leq X _ 2\)，\(Y _ 1 \leq y \leq Y _ 2\) 且 \(x, y\) 均为整数时

\[f(x, y) = (A x ^ 3 + B y ^ 3 + C x ^ 2 y + Dxy ^ 2 + Exy + Fx + Gy) \bmod P \]

的最大值。

输入格式

输入共一行十二个整数 \(A, B, C, D, E, F, G, P, X_1, X_2, Y_1, Y_2\)。

输出格式

输出一个整数，代表 \(f(x, y)\) 的最大值。

样例 #1

样例输入 #1

3 2 5 6 1 4 2 998244353 1 2 1 3

样例输出 #1

266

提示

样例解释 #1

当 \(x\) 为 \(1\) 到 \(2\) 之间的整数，\(y\) 为 \(1\) 到 \(3\) 之间的整数时，函数 \(f(x,y)\) 的值如下：

\[f(1,1)=23,\ f(1,2)=63,\ f(1,3)=139\\ f(2,1)=70,\ f(2,2)=144,\ f(2,3)=266 \]

最大值为 \(f(2,3)\)，即 \(266\)。

数据规模与约定

对于 \(100\%\) 的数据，保证 \(1 \leq A, B, C, D, E, F, G, P \leq 10 ^ 9\)，\(1 \leq X _ 1 \leq X _ 2 \leq 10 ^ 3\)，\(1 \leq Y _ 1 \leq Y _ 2 \leq 10 ^ 3\)。

思路

由题意，循环枚举每种可能的\(x,y\)，进行求解\(f\)函数。

代码实现

#include<bits/stdc++.h>
using namespace std;
long long a,b,c,d,e,f,g,p,x1,x2,y1,y2,mx=-1;
long long solve(long long x,long long y)
{
	return ((a*x*x*x)+(b*y*y*y)+(c*x*x*y)+(d*x*y*y)+(e*x*y)+(f*x)+(g*y))%p;
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>a>>b>>c>>d>>e>>f>>g>>p>>x1>>x2>>y1>>y2;
	for(long long x=x1;x<=x2;x++)
	{
		for(long long y=y1;y<=y2;y++)
		{
			mx=max(mx,solve(x,y));
		}
	}
	cout<<mx<<endl;
	return 0;
}

T5 小跳蛙

题目背景

idea 提供者： bj12z_jiasiyuan

验题：卷王

题目描述

有 \(n - 1\) 只小跳蛙在池塘中，依次被编号为 \(1, 2, \cdots, n - 1\)。池塘里有 \(n\) 个位置，每一个位置上有一个数字 \(a_i\)。如果 \(a_i = 0\)，则表示这个位置是一个空位；否则表示这个位置上存在一个编号为 \(a_i\) 的小跳蛙。

接下来的 \(n-1\) 分钟，小跳蛙们将进行跳跃。第 \(i\) 分钟，编号为 \(i\) 的小跳蛙将跳到空位上。

请你输出 \(n-1\) 分钟后池塘中每个位置的数字，即每个位置是否为空、小跳蛙编号是多少。

输入格式

输入共两行。

第一行一个整数 \(n\)。
第二行 \(n\) 个整数 \(a _ 1, a _ 2, \cdots, a _ n\)。

输出格式

输出一行 \(n\) 个整数 \(a _ 1, a _ 2, \cdots, a _ n\)。 表示 \(n-1\) 分钟后池塘的状态。

样例 #1

样例输入 #1

5
1 2 0 3 4

样例输出 #1

2 3 1 4 0

提示

样例解释 #1

  • 第一分钟后池塘状态：0 2 1 3 4
  • 第二分钟后池塘状态：2 0 1 3 4
  • 第三分钟后池塘状态：2 3 1 0 4
  • 第四分钟后池塘状态：2 3 1 4 0

因此最终池塘的状态为 2 3 1 4 0。

数据规模与约定

对于 \(50\%\) 的数据，\(1 \leq n \leq 10 ^ 3\)。

对于 \(100\%\) 的数据，\(1 \leq n \leq 10^6\)，保证序列 \(a\) 是一个 \(0 \sim n - 1\) 这些数字的排列。

思路

每个跳蛙都会跳到每上一个跳蛙跳跃的起始点。换成数学，就是每个元素都\(+1\)，元素\(n-1\)变为\(0\)。

代码实现

#include<bits/stdc++.h>
using namespace std;
int a[1000005],b[1000005];
int main()
{
	ios::sync_with_stdio(false);
	int n;
	cin>>n;
	for(int i=0;i<n;i++)
	{
		cin>>a[i];
		b[i]=a[i]+1;
		if(a[i]==n-1) b[i]=0;
		cout<<b[i]<<" "; 
	}
	return 0;
}

T6 图像变换

题目描述

一张字符图片由 \(n\) 行 \(m\) 列，共 \(n\times m\) 个字符组成，第 \(i\) 行第 \(j\) 列的字符为 \(s_{i,j}\)。如下图所示，为一个 \(4\times 3\) 的字符图片。

%%%
$$$
@w@
!!!

现在，需要将图像放大 \(k\) 倍，得到 \(kn \times km\) 的图片。原图片的每个字符都需要重复 \(k^2\) 次，作为新图像中 \(k\times k\) 的一个区域，各字符的相对位置不变。

将上面给出的例子放大 \(2\) 倍，将得到如下图像：

%%%%%%
%%%%%%
$$$$$$
$$$$$$
@@ww@@
@@ww@@
!!!!!!
!!!!!!

输入格式

输入 \(n+1\) 行。

输入的第一行为三个整数 \(n,m,k\)。

接下来 \(n\) 行，每行 \(m\) 个字符，表示字符图片。

输出格式

输出 \(nk\) 行，每行 \(mk\) 个字符，表示变换后的字符图片。

样例 #1

样例输入 #1

4 3 2
%%%
$$$
@w@
!!!

样例输出 #1

%%%%%%
%%%%%%
$$$$$$
$$$$$$
@@ww@@
@@ww@@
!!!!!!
!!!!!!

提示

数据规模与约定

  • 对于 \(30\%\) 的测试数据，输入的字符画仅包含一种字符；
  • 对于 \(100\%\) 的测试数据，\(1 \le n, m \le 100\)，\(1 \le k \le 10\)，输入的字符仅包含 ASCII 码不超过 127 的可见字符。

思路

事实上，这是将每个字符二维拓展k倍。

代码中，\(i,j\)控制字符坐标，\(v,l\)控制二维放大倍数。

代码实现

#include<bits/stdc++.h>
using namespace std;
char s[102][102];
int main()
{
	ios::sync_with_stdio(false);
	int n,m,k;
	cin>>n>>m>>k;
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<m;j++)
		{
			cin>>s[i][j];
		}
	}
	for(int i=0;i<n;i++)
	{
		for(int v=0;v<k;v++)
		{
			for(int j=0;j<m;j++)
			{
				for(int l=0;l<k;l++)
				{
					cout<<s[i][j];
				}
			}
			cout<<endl;
		}
	}
	return 0;
}

T7 二进制与一

题目描述

给定一个正整数 \(n\)，以及操作次数 \(q\)。对于每次操作，给出一个正整数 \(k\)，要求：让 \(n\) 加上一个非负整数 \(x\)，使得 \(n\) 在二进制下的第 \(k\) 位（从右往左数）是 \(1\)，并在符合要求的情况下，令 \(x\) 最小。

请注意，每次操作都会让 \(n\) 变为 \(n + x\)，会影响后续操作。

小山需要求出，所有的 \(x\) 之和是多少。

输入格式

输入共 \(q + 1\) 行。

第一行两个整数 \(n\) 和 \(q\)。
接下来 \(q\) 行，每行一个正整数 \(k\)，表示要让 \(n\) 在二进制下从右往左数的第 \(k\) 位是 \(1\)。

输出格式

一行一个整数，表示所有的 \(x\) 之和。

样例 #1

样例输入 #1

5 3
2
3
4

样例输出 #1

3

提示

样例 1 说明

\(5\) 在二进制下是 \(101\)。

  • 对于第一次操作，需要让 \(101\) 的第二位变为 \(1\)，则需让 \(101\) 加上 \(1\)，变为 \(110\)；
  • 对于第二次操作，需要让 \(110\) 的第三位是 \(1\)，由于 \(110\) 的第三位本身就是一，所以无需改变；
  • 第三次操作同理，需要让 \(110\) 加上 \(2\)。

最终输出结果是 \(1+0+2=3\)。

数据规模与约定

对于 \(100\%\) 的数据，\(1\le n < 2^{32}，1\le q\le 10^5，1 \le k\le 32\)。

测试点编号 \(n\) \(q\) \(k\)
\(1\) \(\leq 4\) \(\leq 10\) \(\leq 2\)
\(2, 3\) \(\leq 4\) \(\leq 10\) \(\leq 32\)
\(4, 5\) \(\leq 1024\) \(\leq 1000\) \(\leq 10\)
\(6, 7\) \(< 2 ^ {32}\) \(\leq 10\) \(\leq 32\)
\(8 \sim 10\) \(< 2 ^ {32}\) \(\leq 10 ^ 5\) \(\leq 32\)

思路

完善中……

代码实现

To be continued.

T8 Genshin 玩家

题目背景

你说得对，后面忘了。

题目描述

在洛谷入门赛/语言月赛出题 QQ 群里，著名洛谷管理员蓝边铅球老师的群名片是『原神玩家』。

现在，扶苏给了你一个字符串 \(s\)，她想请你求出：有多少种方案可以在 \(s\) 中取出两个子串 \(s[l_1, r_1], s[l_2, r_2]\)，满足：

  • \(1 \leq l_1 \leq r_1 \leq l_2 \leq r_2 \leq |s|\)，这里 \(|s|\) 表示字符串 \(s\) 的长度。
  • \(s[l_1, r_1]\) 表示由 \(s\) 的第 \(l_1\) 个字符到第 \(r_1\) 个字符构成的字符串，\(s[l_1, r_1] = \texttt{Genshin}\)。
  • \(s[l_2, r_2]\) 表示由 \(s\) 的第 \(l_2\) 个字符到第 \(r_2\) 个字符构成的字符串，\(s[l_2, r_2] = \texttt{player}\)。

两个方案不同，当且仅当两个方案中 \(l_1, r_1, l_2, r_2\) 至少有一个对应不同。

输入格式

输入只有一行，表示字符串 \(s\)。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

Genshinplayerplayer

样例输出 #1

2

样例 #2

样例输入 #2

ExpectedIsAGenshinplayerWhoLikesToBeAGenshinplayer

样例输出 #2

3

提示

数据规模与约定

  • 对 \(30\%\) 的数据，保证 \(|s| \leq 50\)。
  • 对 \(60\%\) 的数据，保证 \(|s| \leq 200\)。
  • 对 \(100\%\) 的数据，保证 \(1 \leq |s| \leq 2000\)，\(s\) 中仅含大小写英文字母。

思路

先循环遍历字符串找Genshin的位置，因为player一定要在Genshin后，所以在找到Genshin之后再找player。

代码实现

#include<bits/stdc++.h>
using namespace std;
const string _1="Genshin",_2="player";
int main()
{
	ios::sync_with_stdio(false);
	string s;
	int ans=0;
	cin>>s;
	for(int i=0;i<s.length();i++)
	{
		string str=s.substr(i,7);
		if(str==_1)
		{
			for(int j=i;j<s.length();j++)
			{
				str=s.substr(j,6);
				if(str==_2) ans++;
			}
		}
	}
	cout<<ans<<endl;
	return 0;
}

备注

T7正完善中~~~。

标签：10,洛谷,leq,19,题解,样例,int,输出,饼干
From： https://www.cnblogs.com/j1hx-oi/p/17975649

相关文章

  • 南外集训 2024.1.19 T3
    给定正整数\(m,n\)使得\(m|n\)，求\([1,n]\cap\mathbbZ\)的所有子集中有多少和是\(m\)的倍数。\(1\leT\le10^4,1\lem\le10^7,1\len\le10^{18}\)相当于求\(F(z)=(1+z^0)(1+z^1)\dots(1+z^{n-1})\)的\(0,m,2m,\dots\)项之和。单位根反演可得\(Ans=......
  • AGC019F Yes or No
    洛谷AT思路先思考最优策略是什么，如果你想尽可能多的对，那么一定是答当前剩的数目最多的答案。比如当前还有\(x\)道\(\text{YES}\)，\(y\)道\(\text{NO}\)，在\(x>y\)时一定答\(\text{YES}\)，\(x<y\)时一定答\(\text{NO}\)，\(x=y\)时两者皆可，不妨设他都选\(\text{YES}\)。......
  • 闲话1.19
    摆。上午模拟赛摆了，哈哈，交都没交......
  • 题解 CF1909H
    题意给定一个长度为\(n\)的排列\(p\)。你可以进行不超过\(10^6\)次操作，每次操作是选择一个长度为偶数的区间\([l,r]\)，然后交换\((p_l,p_{l+1}),(p_{l+2},p_{l+3}),...,(p_{r-1},p_r)\)。你需要将排列排序。数据范围：\(n\le3\times10^5\)。题解刚才有个群友问我Z......
  • $20240119$ 练习题解
    \(20240119\)练习题解CF472D通过尝试我们容易发现，与点\(1\)最近的点一定是直接儿子。我们要是把它作为突破点，那就成功了一半了。假设点\(2\)与点\(1\)最近，又假设我们可以用函数\(F(x)\)来确定\(x\)点的子树形态。那我们会发现如果我们还有剩余的节点，那么剩余的节点......
  • 1.19 _fetchSql() 和 getLastSql() 的用法
    1fetchSql()的用法重要点：语法2getLastSql()的用法删除不掉的原因具有外键的那张表叫：主表，也就是details是主表，internet_bar这个是从表当使用:DELETEFROMbusiness_internet_barwhereid=34;删除表中的数据的时候,会发生下面的错误DELETEFROM`business_in......
  • Linked list reversal using stack【1月19日学习笔记】
    点击查看代码//Linkedlistreversalusingstack#include<iostream>#include<stack>//stackfromstandardtemplatelibrary（STL）usingnamespacestd;structnode{ chardata; node*next;};node*A;//全局头指针voidreverse(){ if(A==NULL)return;//空......
  • 2024-1-19阻止事件
    目录阻止事件没有添加阻止事件：添加阻止事件区别点：阻止事件为什么要有阻止事件这里有个情况，但我的输入框内没有输入字符串就被提交的时候，我需要它显示提示文字，但是如果没有阻止事件的参与就有可能无法长久显示没有添加阻止事件：例子如下<!DOCTYPEhtml><html> <head> <met......
  • string reversal using stack【1月19日学习笔记】
    点击查看代码//stringreversalusingstack#include<iostream>#include<stack>//stackfromstandardtemplatelibrary（STL）usingnamespacestd;voidreverse(char*c,intn){ stack<char>S; for(inti=0;i<n;i++){ S.push(c[i]);//st......
  • 2024.1.19寒假每日总结10
    算法题：2809.使数组和小于等于x的最少时间-力扣（LeetCode）spark广播器场景:本地集合对象和分布式集合对象(RDD)进行关联的时候需要将本地集合对象封装为广播变量可以节省:1.网络IO的次数2.Executor的内存占用 ......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99