\(20240119\) 练习题解

CF472D

通过尝试我们容易发现，与点 \(1\) 最近的点一定是直接儿子。我们要是把它作为突破点，那就成功了一半了。

假设点 \(2\) 与点 \(1\) 最近，又假设我们可以用函数 \(F(x)\) 来确定 \(x\) 点的子树形态。那我们会发现如果我们还有剩余的节点，那么剩余的节点中与 \(1\) 最近的也是它儿子，这样反复就能确定该树。所以我们要尝试思考该函数。

我们发现 \(F(x)\) 的目的好像也可以用“找最近的儿子”方法解决，但是新的困难是：我们可能还会有子树外的点。我们只需确定某点 \(y\) 是否在子树 \(x\) 内 \((x > 1)\)。设 \(x\) 的父节点为 \(fa\)。那么：

• 若是，则有 \(dis_{fa, y}-dis_{x, y}=dis_{fa, x}\)；
• 否则，有 \(dis_{fa, y}-dis_{x, y}=-dis_{fa, x}\)。

于是就解决了。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e3 + 5;
int ok[N], n, a[N][N], fa[N];
bool dfs(int u, int pre){
	ok[u] = 1;
	while(1){	
		int Min = INT_MAX, tmp = 0;
		for(int i = 1; i <= n; i++){
			if(abs(a[pre][i] - a[u][i]) != a[pre][u]) return 1;
			if(!ok[i] && a[pre][i] - a[u][i] == a[pre][u] && Min > a[u][i]) Min = a[u][i], tmp = i;
		}
		if(!tmp) break;
		fa[tmp] = u;
		if(dfs(tmp, u)){
			return 1;
		}
	}
	return 0;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){
			cin >> a[i][j];
			if(i == j && a[i][j]){
				cout << "NO" << endl;
				return 0;
			}
			if(i != j && !a[i][j]){
				cout << "NO" << endl;
				return 0;
			}
			if(i > j && a[i][j] != a[j][i]){
				cout << "NO" << endl;
				return 0;
			}
		}
	}
	ok[1] = 1;
	int cnt = 0;
	while(1){
		cnt++;	
		int Min = INT_MAX, tmp = 0;
		for(int i = 1; i <= n; i++){
			if(!ok[i] && Min > a[1][i]) Min = a[1][i], tmp = i;
		}
		if(!tmp) break;
		fa[tmp] = 1;
		if(dfs(tmp, 1)){
			cout << "NO" << endl;
			return 0;
		}
		if(cnt == n + 5){
			cout << "NO" << endl;
			return 0;
		}
	}
	cout << "YES" << endl;
	return 0;
}

CF500E

题意太过复杂，大致为：给定 \(n\) 个区间，每次询问第 \(l\) 个区间的左端到第 \(r\) 个的右端中有几个单位长度未被覆盖。

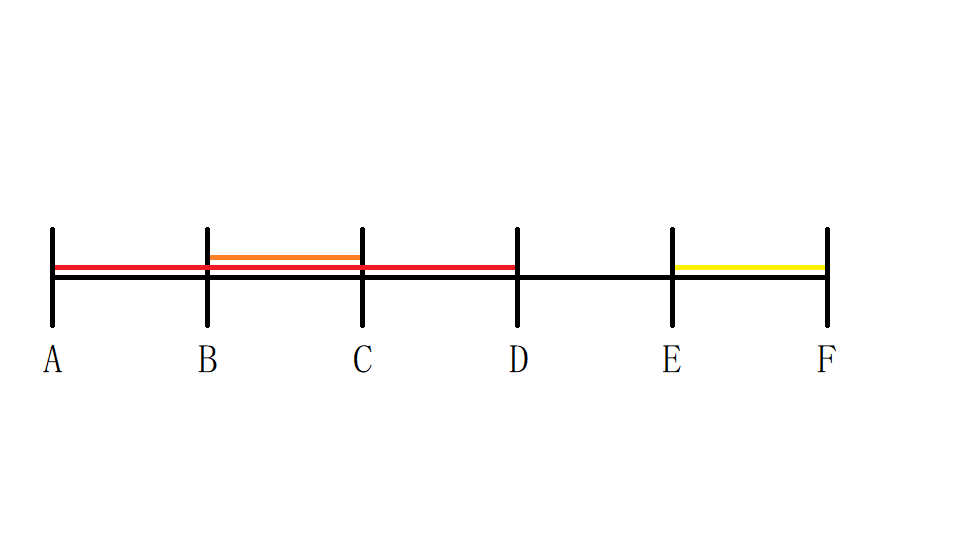
如图，记录：

• \(nxt_i\) 为向右推到 \(i\) 号骨牌后 \(i\) 右侧第一个没倒的，如图 \(nxt_{\text{红}}=\text{黄}\)；
• \(f_i\) 为向右推到后的能到达的最大位置，例如 \(f_{\text{红}}=D\)；
• \(val_i\) 为空缺的单位长度，如 \(val_{\text{红}}=DE=1\)。

接着就倍增就好了。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int n, q, p[N], l[N], f[N], nxt[N][25], val[N][25];
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n;
	for(int i = 1; i <= n; i++)
		cin >> p[i] >> l[i];
	p[n + 1] = INT_MAX;
	nxt[n][0] = n + 1, f[n] = p[n] + l[n];
	for(int i = n - 1; i >= 1; i--){
		nxt[i][0] = i + 1;
		f[i] = p[i] + l[i];
		while(p[i] + l[i] >= p[nxt[i][0]]) f[i] = max(f[i], f[nxt[i][0]]), nxt[i][0] = nxt[nxt[i][0]][0];
	}
	for(int i = n; i >= 1; i--){
		if(nxt[i][0] == n + 1) continue;
		val[i][0] = p[nxt[i][0]] - f[i];
	}
	nxt[n + 1][0] = n + 1;
	for(int i = 1; i <= 20; i++){
		for(int j = n; j >= 1; j--){
			nxt[j][i] = nxt[nxt[j][i - 1]][i - 1];
			val[j][i] = val[j][i - 1] + val[nxt[j][i - 1]][i - 1];
		}
		nxt[n + 1][i] = n + 1;
	}
	cin >> q;
	int ans = 0, l, r;
	while(q--){
		ans = 0;
		cin >> l >> r;
		for(int i = 20; i >= 0; i--)
			if(nxt[l][i] <= r)
				ans += val[l][i], l = nxt[l][i];
		cout << ans << endl;
	}
	return 0;
}

CF241E

蛮好，抽象的。

发现一条边只能是 \(1\) 或 \(2\)，然后：

直接差分约束。

确实蛮好。

#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 1e6;
int cnt, a[N], b[N], c[N], n, m, dis[N], ok[N], used[N];
int s1[N], s2[N];
vector<int> g[N];
void addEdge(int x, int y, int z){
	cnt++, a[cnt] = x, b[cnt] = y, c[cnt] = z;
	return ;
}
void dfs(int u){
	used[u] = 1;
	if(u == n){
		ok[u] = 1;
		return ;
	}
	for(int v : g[u]){
		if(used[v]){
			ok[u] |= ok[v];
			continue;
		}
		dfs(v);
		ok[u] |= ok[v];
	}
	return ;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for(int i = 1; i <= m; i++){
		int x, y;
		cin >> x >> y;
		g[x].push_back(y);
		s1[i] = x, s2[i] = y;
	}
	dfs(1);
	for(int i = 1; i <= m; i++)
		if(ok[s1[i]] && ok[s2[i]])
			addEdge(s1[i], s2[i], 2), addEdge(s2[i], s1[i], -1);
	for(int i = 1; i <= n; i++) dis[i] = 1e9;
	dis[1] = 0;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= cnt; j++){
			dis[b[j]] = min(dis[b[j]], dis[a[j]] + c[j]);
		}
	}
	for(int i = 1; i <= cnt; i++){
		if(dis[b[i]] > dis[a[i]] + c[i]){
			cout << "No" << endl;
			return 0;
		}
	}
	cout << "Yes" << endl;
	for(int i = 1; i <= m; i++){
		if(ok[s1[i]] && ok[s2[i]])
			cout << dis[s2[i]] - dis[s1[i]] << endl;
		else
			cout << 2 << endl;
	}
	return 0;
}

CF41D

更抽象了，因为随机，所以直接暴力 \(1\) 到 \(24\) 的数，代码不放了。