
$upd:$2024.1.19改正了一些错误
题目讲解 只看第三题
若在三角板开始转动的同时,射线\(OC\)也绕点\(O\)以每秒25°的速度逆时针旋转一周,从旋转开始多长时间,射线\(OC\)平分\(∠BOD\)?
最重要的一点:
动角角度 \(=\) 初始值 \(+\) 角度\((vt)\)
明确了这一点之后
我们看题
这题可以分为三种可能
情况1:
图就是图一:
由已知可得:\(OC\)平分\(∠BOD\)
∴ \(∠BOD = 2∠COD\)
根据题意:我们知道\(∠BOD\)初始为\(90\),\(∠COD\)初始为\(30\)
那么根据公式,我们可以得出:
当所有的角都如图一所示时:
\(∠BOD = 90 + 20t\)
\(∠COD = 40 + 25t\)
显然我们可以得出:
\(90 + 20t = 2(40 + 25t)\)
解得$t= $ $ 1 \over 3$
情况2:
如图所示: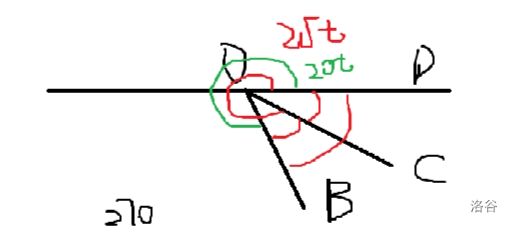
如图所示:\(OC\)转了一圈转到了\(OD\)下面
因为题面中有一句话:本题中的角均大于\(0\)小于\(180\)
所以当\(OB\)转过直线的时候,\(∠BOD=360-(90+20t)=270-20t\)
也就是图中减掉了绿色部分下的\(∠BOD\)
同理,\(∠COD=360-(40+25t)=320-25t\)
∵\(OC\)平分\(∠BOD\)
∴\(∠BOD=2∠COD\)
故\(270-20t=2(320-25t)\)
解得\(t=\) \(37 \over 3\)
情况3:
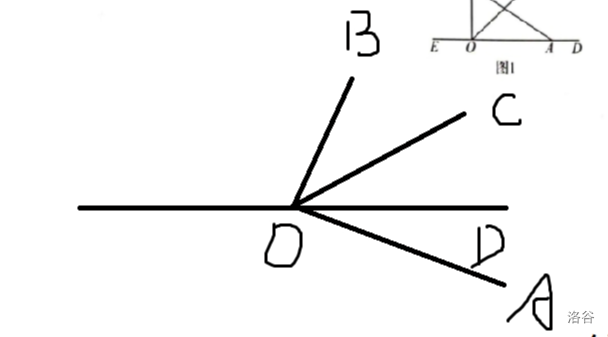
如图所示:\(OC\)回到了起始位置
∵\(OC\)平分\(∠BOD\)
∴\(∠BOC = ∠COD = 40\) 且 \(∠AOB=90\)
又∵\(∠AOD=∠BOA-∠BOC-∠COD\)
∴\(∠AOD=90-40-40=10\)
根据公式,得\(∠AOD=360-20t\)
\(P.S\) 因为\(∠AOD\)最开始的时候是零度角
可得:\(360-20t=10\)
解得\(t=17.5\)
综上所述,\(t=\) \(1 \over 3\) 或 \(t=\) \(37 \over 3\) 或 \(t=17.5\)
\(upd:\) \(vx:18066864787\) \(or\) \(z10y12h14\)获取视频版题解
标签:20t,动角,题解,OC,40,GD,COD,90,BOD From: https://www.cnblogs.com/zhaoyihang/p/17975720