例题1.ACwing 301
为了方便,我们记 \(c_i\) 为c的前缀和,\(t_i\) 同理。
容易推出 \(O(n ^ 2)\) 方程:
\(dp_{i} = \min_{j=0}^{i-1}{(dp_j+s\times (c_n-c_j)+t_i\times (c_i-c_j))}\)
但是本题的数据范围是 3e5,所以考虑优化。
我们先把min给拆掉:
\(dp_i=dp_j+s\times c_n-s\times c_j=t_i\times c_i-t_i\times c_j\)
然后将其转为一个一次函数的形式:
\(dp_j=(s+t_i)c_j+dp_i-s\times c_n-c_i\times t_i\)
我们发现此时可以通过数学方法求出 \(dp_i\),但是我们要求最小。
此时不妨把每个 \((dp_j,c_j)\) 放在平面直角坐标系上。
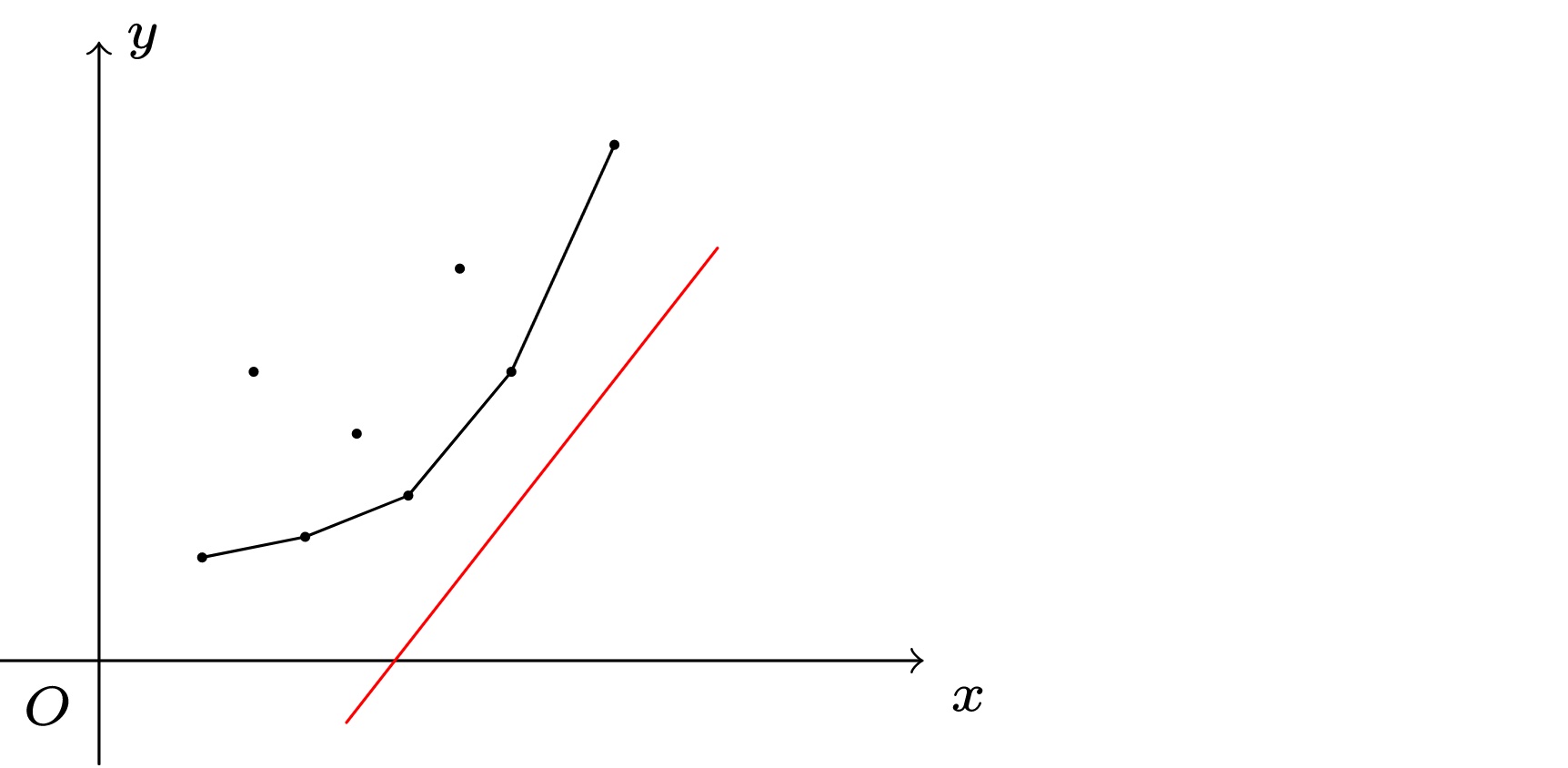
图上黑点即上文所提到的点对,红色线则是此时斜率的代表。
我们要找到一个j,使得 \(dp_i\) 最小,即在图中将红线不断网上平移碰到第一个碰到的点。考虑挖掘这些点的性质,容易发现他们实际上就是一个下凸包,考虑维护下凸包,此时还有一个性质,记 \(k_i\) 表示 在凸包上相邻两点的连线的斜率,那么最优决策点就是第一个大于红线斜率的 \(k_i\) 的右端点。这时我们已经可以用二分去获取答案了,但是注意到本题还有一个性质就是对于单调递增的 \(i\) ,他的斜率也是单调递增的,而且每一次新加的点的横坐标也是单调递增的,那么我们可以直接用维护凸包的队列来获取答案。
查询:因为斜率单调递增,所以如果队头的斜率比现在的斜率小,那么把队头扔掉。
添加:因为横坐标单调递增,所以每一个新算出来的i都要加到下凸包里,但是如果队尾两点的斜率比该点到队尾连线的斜率大的话队尾就要扔掉。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e5 + 5;
int n , s , t[N] , c[N] , dp[N] , q[N] , hh = 1 , tt = 1;
signed main()
{
cin >> n >> s;
for(int i = 1;i <= n;i ++)
{
cin >> t[i] >> c[i];
t[i] = t[i - 1] + t[i];
c[i] = c[i - 1] + c[i];
}
for(int i = 1;i <= n;i ++)
{
while(hh < tt && dp[q[hh + 1]] - dp[q[hh]] <= (t[i] + s) * (c[q[hh + 1]] - c[q[hh]]))hh ++;
int j = q[hh];
dp[i] = dp[j] - (s + t[i]) * c[j] + s * c[n] + c[i] * t[i];
while(hh < tt && (dp[q[tt]] - dp[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (dp[i] - dp[q[tt]]) * (c[q[tt]] - c[q[tt - 1]]))tt --;
q[++ tt] = i;
}
cout << dp[n] << '\n';
return 0;
}
接下来,我们考虑加强版怎么去做。即P5782。
注意到区别就是此时 \(t_i\) 是可以取到负数的。那么这就意味着斜率不在是单调递增的了,但是由于 \(c_i\) 是单调递增的,所以我们每次只能去二分获取答案。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e5 + 5;
int n , s , hh = 1 , tt = 1 , q[N] , t[N] , c[N] , dp[N];
bool check(int mid , int i)
{
return (dp[q[mid + 1]] - dp[q[mid]]) > (s + t[i]) * (c[q[mid + 1]] - c[q[mid]]);
}
int search(int i)
{
int l = hh , r = tt , ans;
while(l < r)
{
int mid = l + r >> 1;
if(check(mid , i))ans = mid , r = mid;
else l = mid + 1;
}
return q[r];
}
signed main()
{
cin >> n >> s;
for(int i = 1;i <= n;i ++)cin >> t[i] >> c[i];
for(int i = 1;i <= n;i ++)t[i] = t[i - 1] + t[i] , c[i] = c[i - 1] + c[i];
for(int i = 1;i <= n;i ++)
{
int j = search(i);
dp[i] = dp[j] - (s + t[i]) * c[j] + s * c[n] + c[i] * t[i];
while(hh < tt && (dp[q[tt]] - dp[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (dp[i] - dp[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt --;
q[++ tt] = i;
}
cout << dp[n] << '\n';
return 0;
}