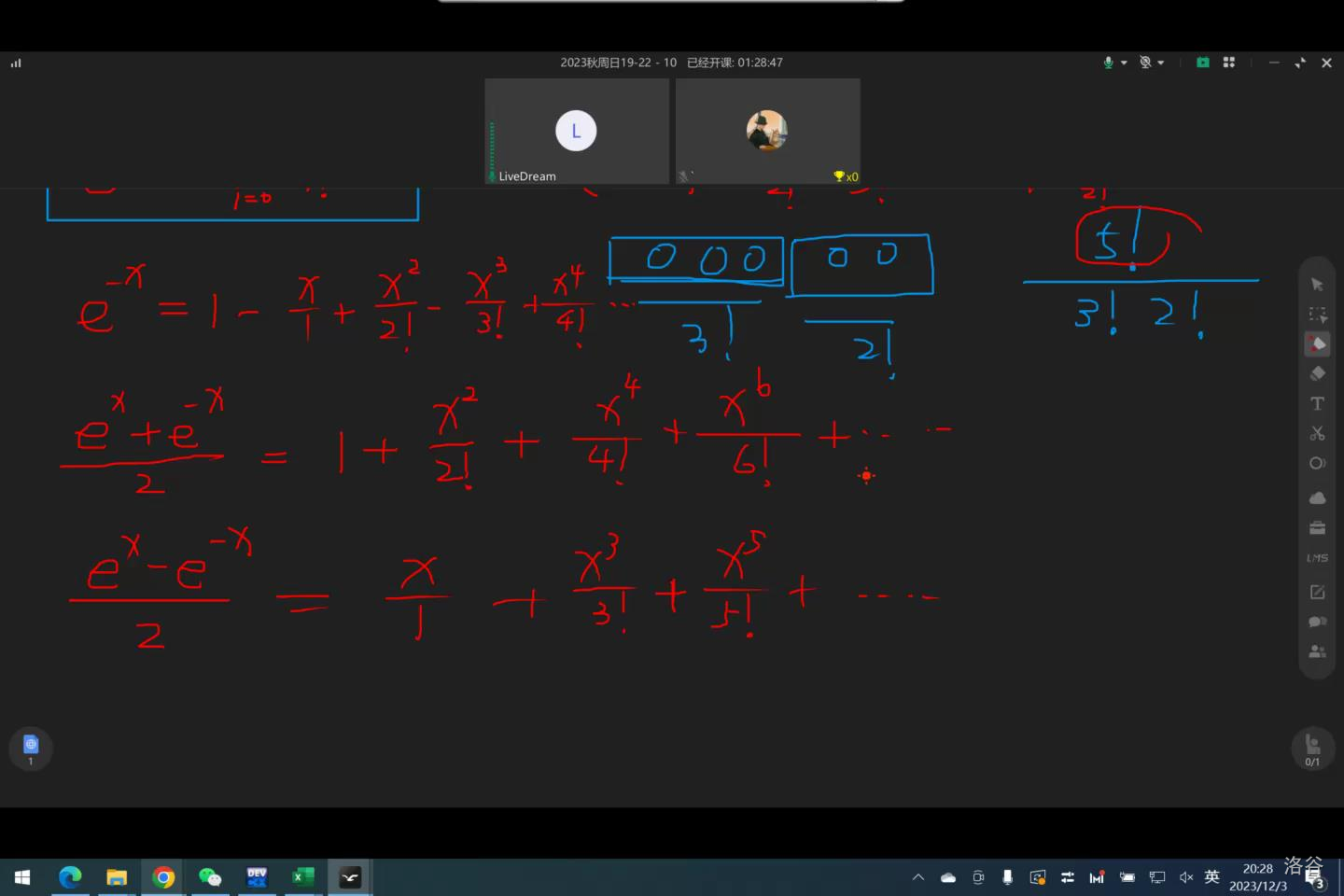
使用场景:无穷级数与函数的对应。
无穷级数:一个无限的数列的和。
生成函数的应用:
- 求组合
- 求排列
普通型生成函数:
\(g(x)=\sum_{i=0}^\infty a_ix_i\)
常见的普通型生成函数:
\(\sum_{i=0}^\infty x^i=\frac{1}{1-x}\)
牛顿二项式定理:
若 \(0\le|a|<|b|\),且 \(n\) 是实数,则有 \((1+x)^n=\sum_{i=0}^\infty C_n^i x^i\)
\(\frac{1}{(1-x)^n}=\sum_{i=0}^\infty C_{n+i-1}^i x^i\)
指数型生成函数:
设 \(g(x)=\sum_{i=0}^na_i\frac{x^i}{i!}\)
\(e^x=\sum_{i=0}^\infty \frac{x^i}{i!}\)
主要的: