MOSFET结构和特性
MOSFET的结构如下:
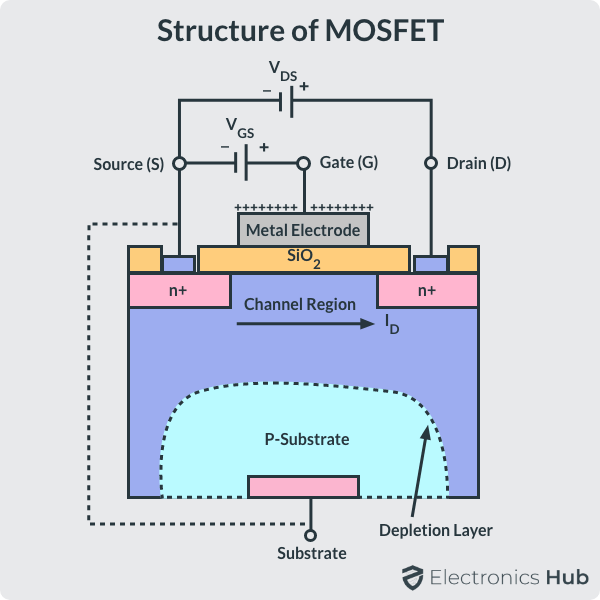
MOSFET的等效电路图如下:
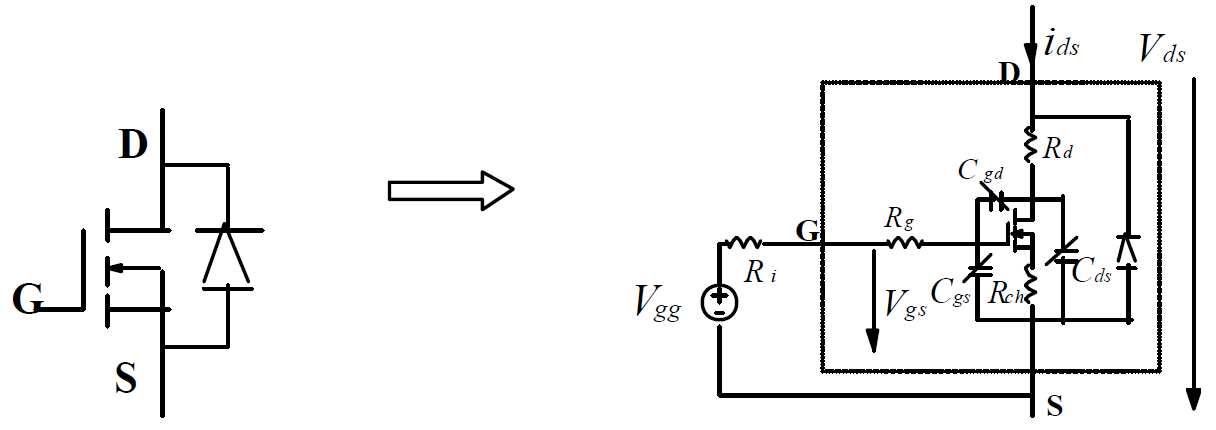
为什么MOSFET的等效电路图中包括了电容?
MOSFET的栅极和漏极、源极之间通过一层薄氧化物如SiO2隔离,但这层绝缘层非常薄,尤其是栅极和源极之间,通常小于一微米厚,以埃为单位测量。这意味着栅极和源极、漏极之间存在相当大的电容,尤其是\(C_{GS}\)非常大。
同时DG、DS之间也存在了相对较小的非线性电容。
MOSFET杂散电容值的大小关系和数量级?
计算MOSFET非线性电容介绍了MOSFET杂散电容的数量级随VDS的变化关系,如下图所示。

其中\(C_{ISS}=C_{gs}+C_{dg}\),\(C_{OSS}=C_{dg}+C_{ds}\),\(C_{RSS}=C_{gd}\)。
从图中可以看出,当\(V_{DS}\)较大时,\(C_{gs}>>C_{ds},C_{gs}>>C_{dg}\),当\(V_{DS}\)较小时,\(C_{gd}\)相对较大,这会加重米勒效应。
在TI的MOSFET和IGBT栅极驱动器电路的基本原理的第10-11页详细介绍了MOSFET开通和关断过程,可注意到米勒效应。
在详谈米勒效应对MOSFET开关过程中的影响介绍了米勒效应造成的米勒平台和误导通现象。
杂散电容造成的影响有什么?
其中米勒平台直接影响了MOSFET的开关速度。同时为了避免误导通,需要人为限制MOSFET的关断速度。而MOSFET开通速度往往由较慢的另一边的二极管的反向恢复速度决定,一般来说不关注。
除此之外,杂散电容与PCB的线路杂散电感存在震荡和误导通问题,也会影响MOSFET开关速度。
杂散电容会造成直接能量损失。包括驱动损耗、\(E_{oss}\)损耗等。其带来的开关速度限制也会增加开关损耗。
为什么米勒效应限制了MOSFET的开关速度?

米勒效应会带来充电时间的延长和米勒平台时间。
当开关管开通过程中,\(C_{gs}\)和\(C_{gd}\)是并联关系,驱动电流需要给\(C_{gs}+C_{gd}\)充电使得\(V_{gs}\)达到合适的电压。
除此之外,当开关管开通时,驱动电流还需要给\(C_{gd}\)充电使得\(V_{DG}\)电压能够降低,进而使得\(V_{DS}\)电压降低,使得开关管从饱和区进入线性区,以达到导通状态。
这会带来米勒平台现象,且电压\(V_{DS}\)越高,米勒平台所需的时间需要的越多,开通速度受限制。
但考虑到\(C_{gd}\)随\(V_{DS}\)的变化关系,\(V_{DS}\)越大,\(C_{gd}\)越小,故米勒平台所需时间与\(V_{DS}\)的关系灵敏度下降了。
开关管关断过程与开通过程刚好相反,有同样的原理。
因此,由于需要给\(C_{gd}\)充电和米勒平台的影响,米勒效应限制了MOSFET的开关速度。
为什么米勒效应带来MOSFET的开关损耗增加?
对MOSFET的开通过程来说,其开启过程损耗计算如下:
\(t_0 - t_2\),在给\(C_{gs}+C_{gd}\)充电使得\(V_{gs}\)达到合适的电压,此时\(V_{DS}\)较大,\(C_{gd}\)较小,充电时间与\(C_{gd}\)关系不大。此阶段损耗功率可近似为$(V_{GS} * C_{gs})/I_{G} * 1/2 V_{DS} * I_D=Q_g/I_G* 1/2 I_DV_{DS} $ 。一般来说,直接用 \(Q_g\) 算出的损耗仅为该段时间的损耗(认为Cgd不变)。
\(t_2 - t_3\),是米勒平台过程,当米勒平台时间较大时,此阶段损耗功率可近似为\((V_{DG} * C_{dg})/I_{G} * 1/2 V_{DS} I_D\),当电压等级较高时,预估损耗需要考虑米勒平台带来的损耗。
\(t_3 - t_4\),在给\(C_{gs}+C_{gd}\)充电使得\(V_{gs}\)进一步增大,此时时间虽然与\(C_{gd}\)关系较大,但此时\(V_{DS}\)较小,\(V_{DS}* I_D\)较小,损耗较小,影响不大。
对MOSFET的关断过程来说,其过程与开通过程刚好相反。
除此之外,在高频时,驱动损耗也是必须考虑的,米勒效应会带来驱动损耗的增加。
标签:11,MOSFET,gs,未完结,米勒,gd,电容,DS From: https://www.cnblogs.com/EvaKo/p/17844507.html