最小生成树

引入

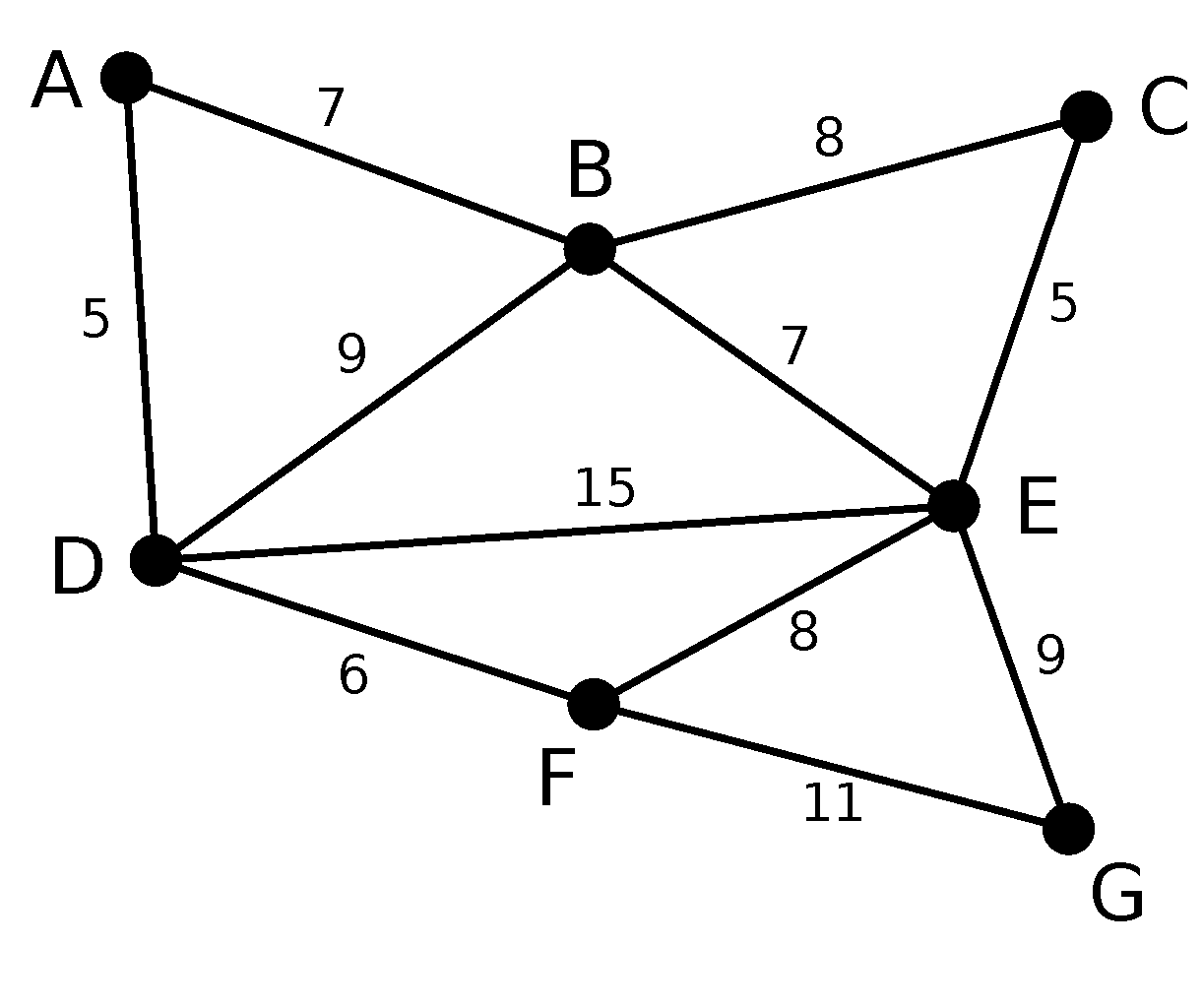
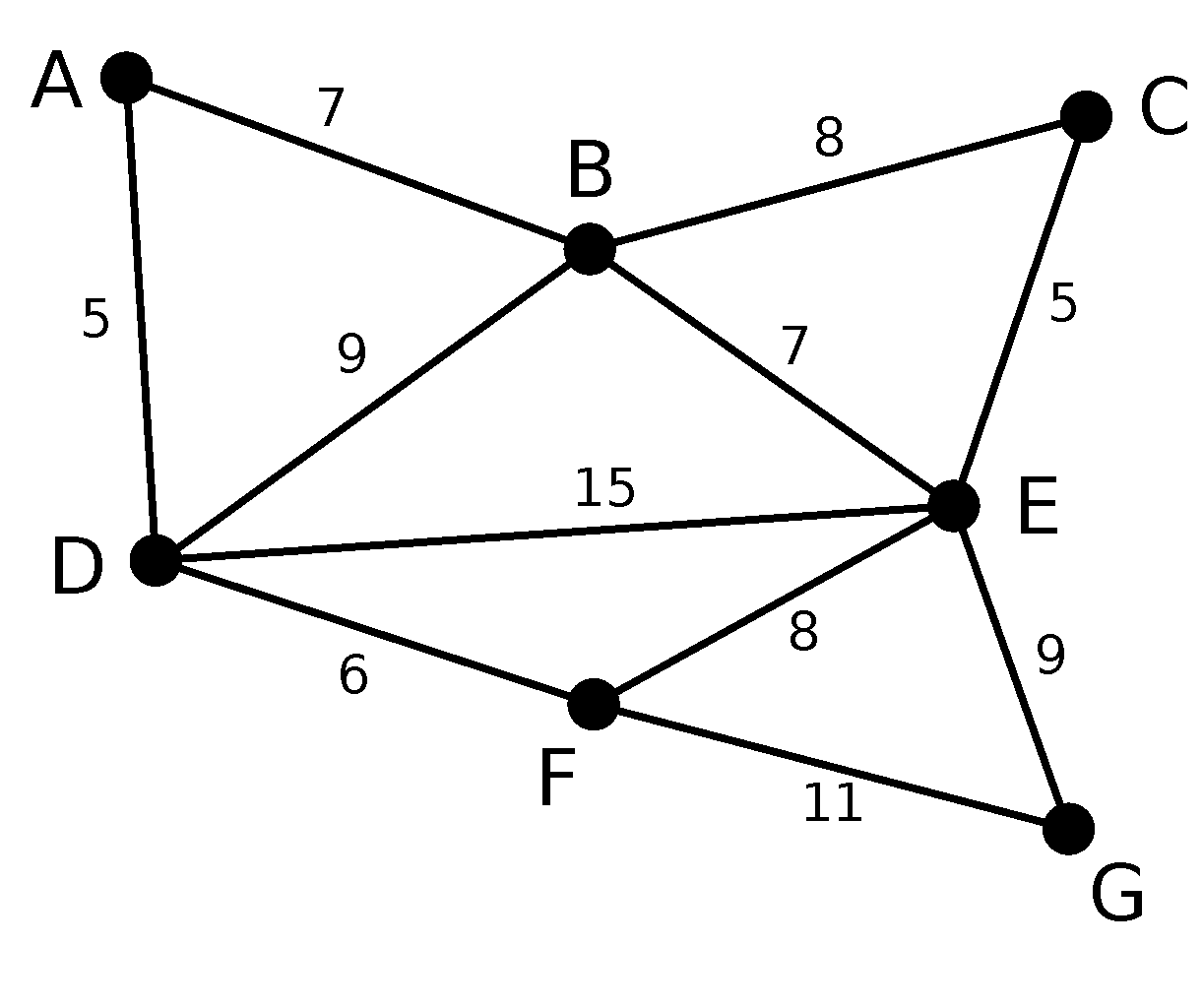
我们定义无向连通图的 最小生成树（Minimum Spanning Tree，MST）为边权和最小的生成树。

注意：只有连通图才有生成树，而对于非连通图，只存在生成森林。

实现

求最小生成树的算法有 Prim 和 Kruskal 两种。这里我们主要讲解 Kruskal 算法（其实是因为太菜了不会 Prim）。

Kruskal 算法

该算法的基本思想是从小到大加入边，是个贪心算法。

先来看一道板子题。

洛谷 P3366 【模板】最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 \(N,M\)，表示该图共有 \(N\) 个结点和 \(M\) 条无向边。

接下来 \(M\) 行每行包含三个整数 \(X_i,Y_i,Z_i\)，表示有一条长度为 \(Z_i\) 的无向边连接结点 \(X_i,Y_i\)。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

不难看出这道题是让我们求最小生成树（这不是废话嘛？）。

我们首先采用直接存边的方式存图。

struct edge{
    int u, v, w;
    bool friend operator<(edge &a, edge &b){
        return a.w < b.w;
    }
}e[MAXM];

for(int i = 1 ; i <= m ; i ++)
    e[i].u = read(),e[i].v = read(),e[i].w = read();

这里我们采用结构体的形式并对运算符进行了重载操作，将每一条边都按权值进行排序。

之后用贪心的思想优先选取权值较小的边，并依次连接，直到已经使用的边的数量比总点数少一即可。

证明：

刚刚有提到：如果某个连通图属于最小生成树，那么所有从外部连接到该连通图的边中的一条最短的边必然属于最小生成树。

所以不难发现，当最小生成树被拆分成彼此独立的若干个连通分量的时候，所有能够连接任意两个连通分量的边中的一条最短边必然属于最小生成树。

证毕。

    for(int i = 1 ; i <= n ; i ++)f[i] = i;
    sort(e + 1, e + m + 1);
    for(int i = 1 ; i <= m ; i ++){
        if(find(e[i].u) != find(e[i].v))
            cnt++,ans += e[i].w,f[find(e[i].u)] = find(e[i].v);
        if(cnt == n - 1)break;
    }

这里给出上面板子题的 AC 代码：

#include <iostream>
#include <algorithm>
#define MAXN 5005
#define MAXM 200005
using namespace std;
int n, m;
struct edge{
    int u, v, w;
    bool friend operator<(edge &a, edge &b){
        return a.w < b.w;
    }
}e[MAXM];
int f[MAXN], cnt, ans;
int read(){
    int t = 1, x = 0;char ch = getchar();
    while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
    while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * t;
}
int find(int x){
    if(f[x] == x)return x;
    else return f[x] = find(f[x]);
}
int main(){
    n = read();m = read();
    for(int i = 1 ; i <= m ; i ++)
        e[i].u = read(),e[i].v = read(),e[i].w = read();
    for(int i = 1 ; i <= n ; i ++)f[i] = i;
    sort(e + 1, e + m + 1);
    for(int i = 1 ; i <= m ; i ++){
        if(find(e[i].u) != find(e[i].v))
            cnt++,ans += e[i].w,f[find(e[i].u)] = find(e[i].v);
        if(cnt == n - 1)break;
    }
    if(cnt < n - 1)cout << "orz" << endl;
    else cout << ans << endl;
    return 0;
}

Prim 算法

对于 Prim 算法，这里仅给出大概实现方法。

Prim 算法是另一种常见并且好写的最小生成树算法。该算法的基本思想是从一个结点开始，不断加点（而不是 Kruskal 算法的加边）。具体来说，每次要选择距离最小的一个结点，以及用新的边更新其他结点的距离。

证明：

Prim算法之所以是正确的，主要基于一个判断：对于任意一个顶点 \(v\)，连接到该顶点的所有边中的一条最短边 \((v, v')\) 必然属于最小生成树（即任意一个属于最小生成树的连通子图，从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树）。

证毕。

小结

两者区别：Prim 在稠密图中比 Kruskal 优，在稀疏图中比 Kruskal 劣。Prim 是以更新过的节点的连边找最小值，Kruskal 是直接将边排序。

两者其实都是运用贪心的思路。

次小生成树

非严格次小生成树

定义

在无向图中，边权和最小的满足边权和 大于等于 最小生成树边权和的生成树

求解方法

• 求出无向图的最小生成树 \(T\)，设其权值和为 \(M\)
• 遍历每条未被选中的边 \(e = (u,v,w)\)，找到 \(T\) 中 \(u\) 到 \(v\) 路径上边权最大的一条边 \(e' = (s,t,w')\)，则在 \(T\) 中以 \(e\) 替换 \(e'\)，可得一棵权值和为 \(M' = M + w - w'\) 的生成树 \(T'\).
• 对所有替换得到的答案 \(M'\) 取最小值即可

如何求 \(u,v\) 路径上的边权最大值呢？

我们可以使用倍增来维护，预处理出每个节点的 \(2^i\) 级祖先及到达其 \(2^i\) 级祖先路径上最大的边权，这样在倍增求 LCA 的过程中可以直接求得。

严格次小生成树

定义

在无向图中，边权和最小的满足边权和 严格大于 最小生成树边权和的生成树

求解方法

考虑刚才的非严格次小生成树求解过程，为什么求得的解是非严格的？

因为最小生成树保证生成树中 \(u\) 到 \(v\) 路径上的边权最大值一定 不大于 其他从 \(u\) 到 \(v\) 路径的边权最大值。换言之，当我们用于替换的边的权值与原生成树中被替换边的权值相等时，得到的次小生成树是非严格的。

解决的办法很自然：我们维护到 \(2^i\) 级祖先路径上的最大边权的同时维护 严格次大边权，当用于替换的边的权值与原生成树中路径最大边权相等时，我们用严格次大值来替换即可。

这个过程可以用倍增求解，复杂度 \(O(m \log m)\)。