邱老师在数学课上留下了一道思考题。
以下是题目简述
已知:
\[\sum _i ^{\infty} \frac{1}{i^2} = \frac{\pi^2}{6} \]求解:
\[\sum _i ^{\infty} \frac{1}{i^2} (2 \ \not| \quad i) \]经过放缩,可以得到一个很是显然的 \(\frac{\pi^2}{8}\)
但是这个解太丑陋了,于是我们尝试去证明 $$\sum _i ^{\infty} \frac{1}{i^2} = \frac{\pi^2}{6} $$
而
参考文献 / 图例 【官方双语】巴塞尔问题:著名公式背后的惊人几何学
当然,这个证明相当粗劣、感性并且不够严谨,但是感性的理解足以让我们体会到巴塞尔问题的巧妙
1 问题的转化
我们可以看到这个标准的代数式上面竟然出现了 \(\pi\),那么说明我们肯定需要转化到几何学的角度上进行分析
故事要从光开始说起。
给出一个很长很长无限长的数轴,我们的眼睛在原点向正方向远眺。
我们在 \(\forall x\in N^+\) 的地方放一个透明且完全一样的灯塔。
那么我们看到的表观亮度也就是数轴上灯塔亮度的和。我们理性的说明,也就是在一个单位时间内,眼睛接受到的光束亮度的大小。
我们假定距离为 \(1\) 的灯塔亮度为 \(1\).
那么你可能会想到各种各样的物理学公式,但是问题求解的确实平方级数。
那么我们考虑重新排列这一个一个灯塔,使在不改变表观亮度的情况下得到一个我们期望获得的解。
华罗庚曾说过“学习数学要善于退,足够地退,退到最原始而不失重要性的地方,是学好数学的一个诀窍。 ”
我们来想想亮度是什么。“什么是亮度呀?”
在脑海中,构建一座灯塔,构建一个直线。就像是下面的这幅图一样。

这根直线也就是数轴上的眼睛,投在这个直线上的光束数量也就是眼睛所接收到的表观亮度。
那么我们可以借助平方反比定律,来理解一下这件事情。
平方反比定律
我们想想,把上面的直线具象为一个平面,那么这个平面所碰到的光束数量同样也是眼睛所接收到的表观亮度。
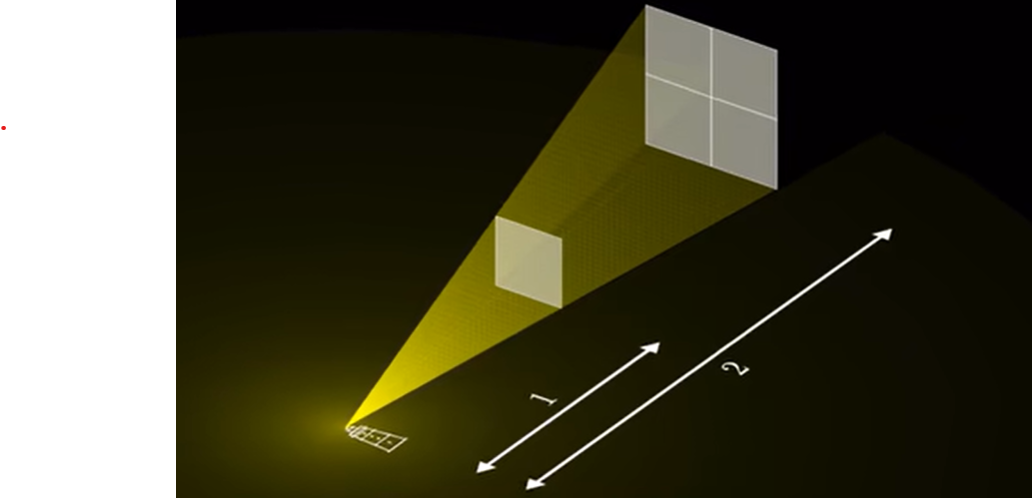
那么,延伸以后的亮度也就是第一个的平方
依照这个定律,我们可以得到在第 \(x\) 远的灯塔的表观亮度也就是 \(x^{-2} = \frac{1}{x^2}\)
那么,我们的问题也就可以转化为眼睛接收到的所有灯塔的表观亮度和。
2 光源的操作
分裂灯塔,一分为二。
又来想象:一个灯塔在平面直角坐标系上,你在整个坐标系的原点 \(O=(0,0).\) 设这个灯塔的坐标为 \(Q=(x,y)\)
我们连接 \((0,0),(x,y).\) 的线段 \(l_1,\) 然后再做一条垂直于\(l_1\) 的直线 \(l_2.\) 那么我们可以得到两个与 \(x,y\) 轴的点 \(A,B;\)
我们设原点到 \(A,B,Q\) 的距离为 \(a,b,h\) 则亮度分别为 \(\frac{1}{a^2} + \frac{1}{b^2} = \frac{1}{h^2}.\) 也就是倒数勾股定理。
3 直击心脏
\[c_{lake}=2. \]湖泊 灯塔 光线
灯塔放射出了光线,正好坐落在湖泊上
我们展开了无限的遐想
一个足够圆的光滑湖泊,上面坐落着一座灯塔,你也在圆的边上的 \(O\) 处,并且是离灯塔最远的地方
\(Q\) 即是灯塔
我们给定了一个柿子
则
\[\because c_{lake}=2 \]\[\therefore L_{O,Q}=d=\frac{2}{\pi} \]\[E_{Q}=(\frac{2}{\pi}) ^2=\frac{\pi ^ 2}{4} \]向你的远方看去,你好像又在一处更大的湖泊边上,与你极远的地方,还有一座亮着灯的灯塔。\(c_{lake}=4\)
你的心中有且仅有灯塔 \(Q\) , 分裂这座灯塔 \(P\).
你连接了 \(OP\) 线段,作一条垂直于 \(OP\) 的直线 \(MM'.\) 分裂 \(P\) 为 \(MM'\) 与 \(lake\) 的两个交点 \(P,P'.\)
那么此时 \(PP'\) 也就是 \(d_{lake}.\)
我们引入一个"倒数勾股定理":对于一个直角三角形,设两个直角边的长度分别为 \(a,b\),高的长度为 \(h.\)
一定会有 \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{h^2}\)
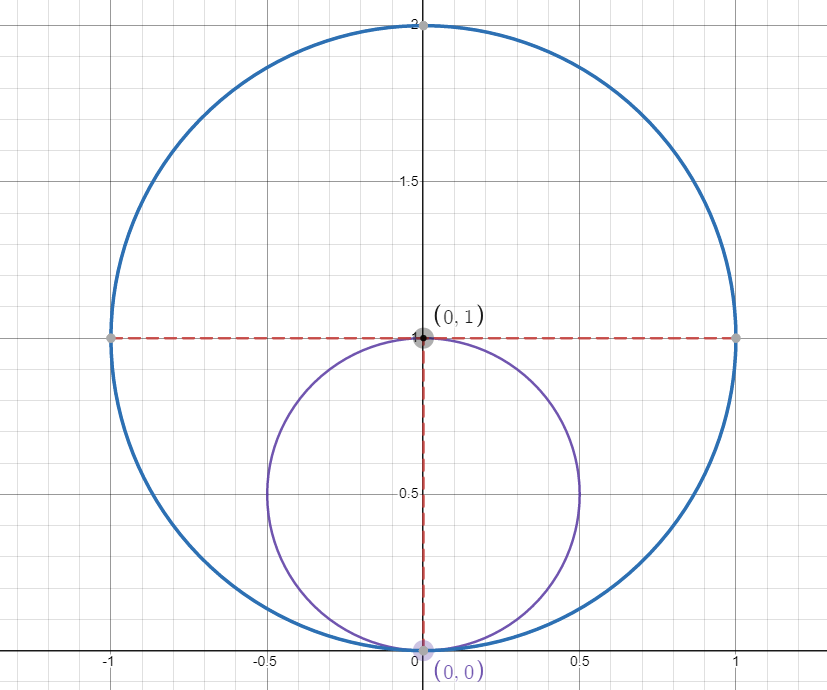
记 \(P_1 =(-1,1) , P_2 = (1,1)\)
然后再连接 \(OP_1 ,OP_2\),利用倒数勾股定理,得到 \(E_{P_1} + E_{P_2} = E_{P}.\)
那么我们就可以拆分 \(P\)
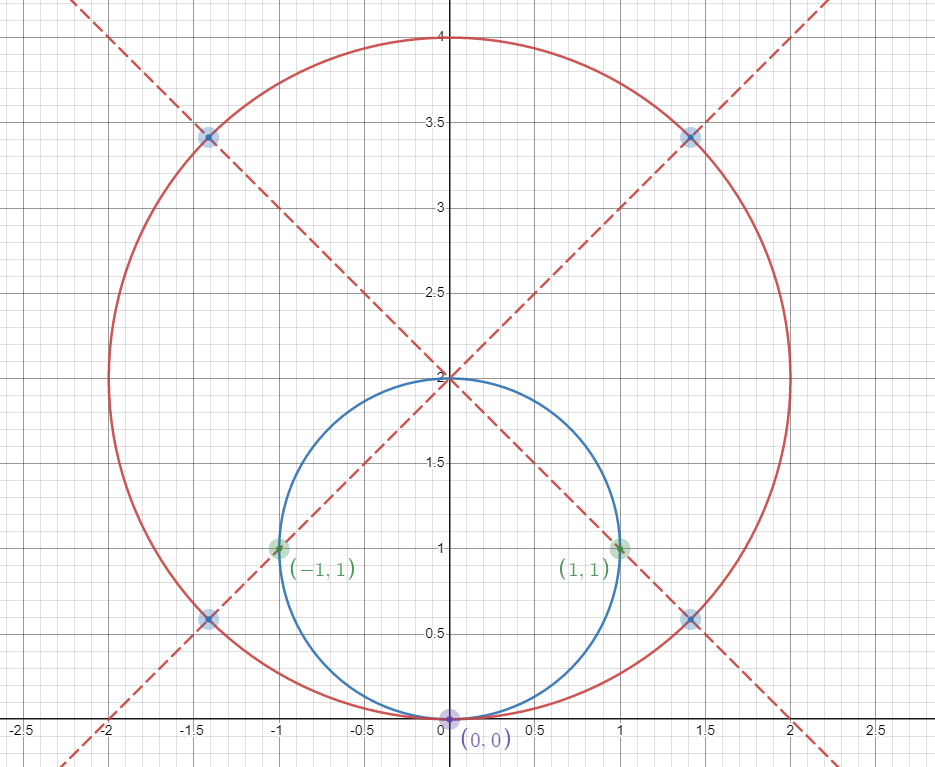
我们可以观察这样一个东西:连接左下角蓝点和 \(O\) ,连接右上角蓝点和 \(O\) , 和两个蓝点的连线可以形成一个三角形.
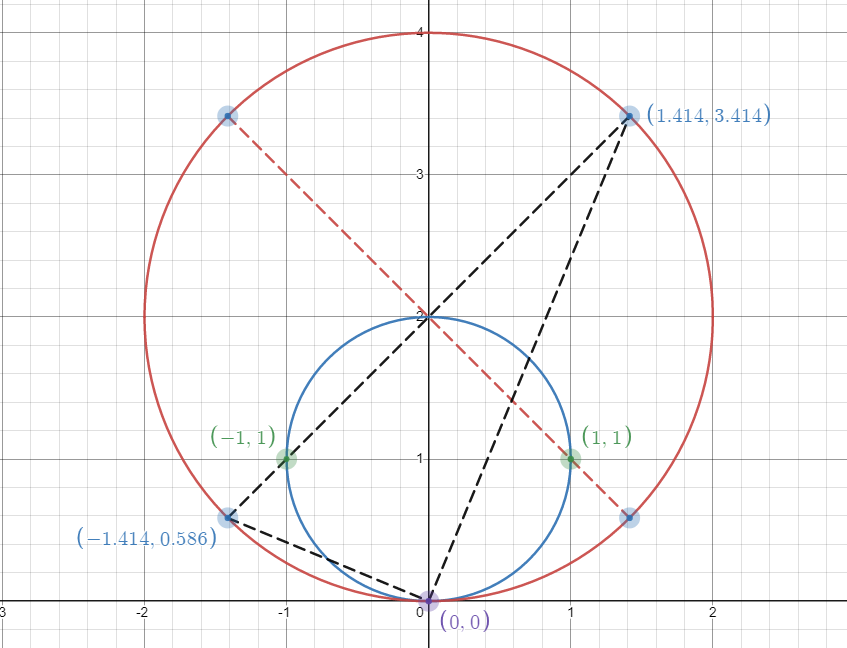
黑色的线段可以构造出一个直角三角形,于是可以像刚才一样采取倒数勾股定理证明绿点可以分裂成蓝点。
然后我们无限地扩大圆的数量以及半径。。。
我们会得到一根无限长的数轴,大概长成这样

现在的答案也就是在 \(O\) 的眼睛接收到的所有灯塔的亮度总和,也就是
\[\sum _{i=1} ^{\infty} \frac{1}{i^2}+\frac{1}{(-i)^2} = \frac{\pi ^ 2}{4} \]然后我们减掉 \(\leftarrow O\) 的负数部分。
可以得到一个很是显然的 \(\frac{\pi^2}{8}\)
然后放缩。
\[The \ End \ Of \ File \] 标签:pi,frac,lake,亮度,证明,问题,巴塞尔,灯塔,我们 From: https://www.cnblogs.com/qxblog/p/Math-Square.html