主席树的定义
主席树,也称可持久化线段树,什么是可持久化线段树呢,即为一颗记录了所有更新过程的线段树。能够处理出从第 $i$ 次更新到第 $j$ 次更新的线段树变化。
前置知识
值域线段树
值域线段树的区间存的并不是节点信息,而是在值在某一范围内的数的个数。
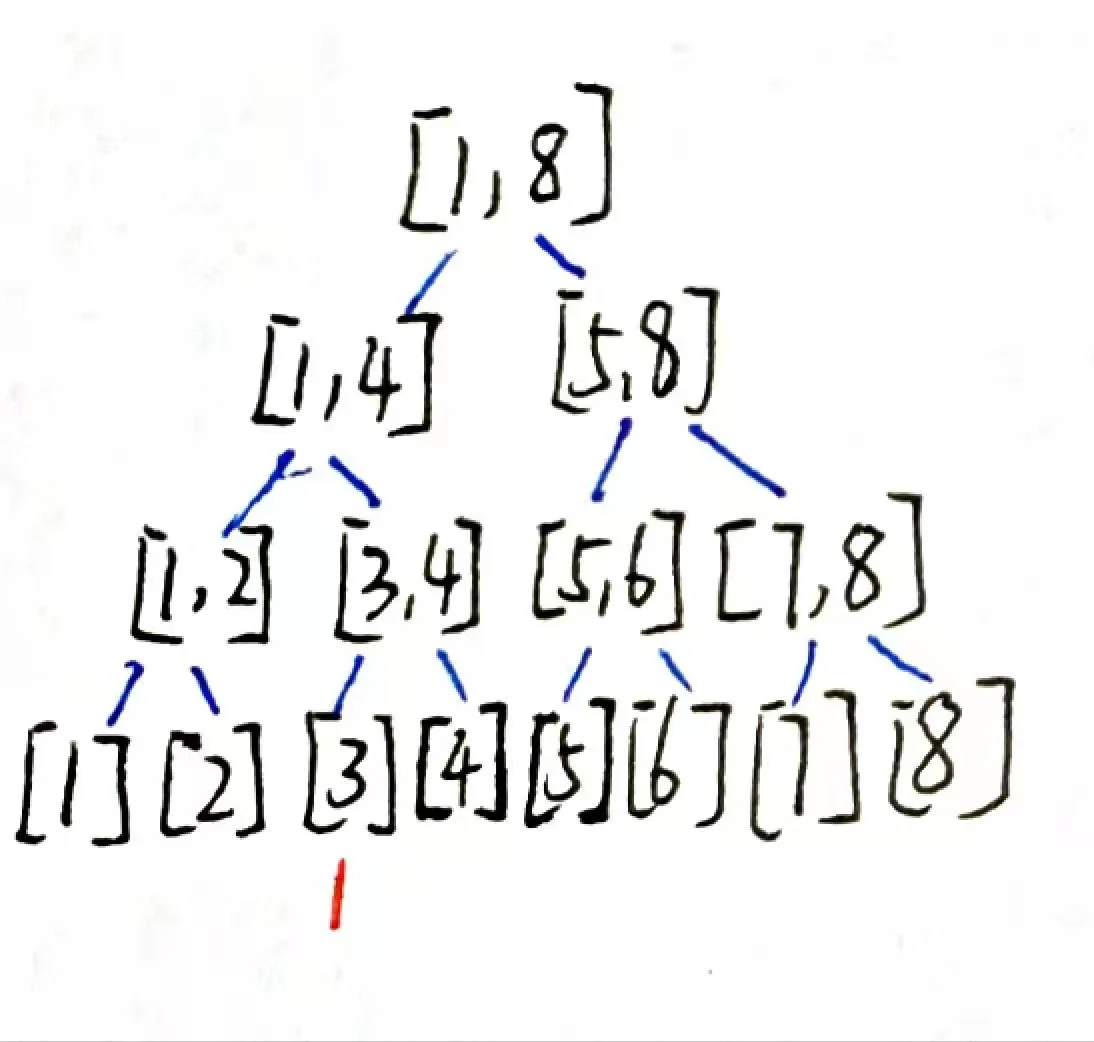
如图就是一棵值域线段树。

1号节点存储的是 大于等于1小于等于4的数字个数
2号节点存储的是 大于等于1小于等于2的数字个数
3号节点存储的是 大于等于3小于等于4的数字个数
4号节点存储的是 等于1的数字个数
5号节点存储的是 等于2的数字个数
6号节点存储的是 等于3的数字个数
7号节点存储的是 等于4的数字个数
查询该区间第 $k$ 大与平衡树相类似,此处不再赘述。
动态开点线段树
原本的线段树我们根据父亲节点为k 子树为k<<1,k<<1|1.
空间复杂度为4N。
现在我们直接存储每个节点的左右儿子。可以有效减少空间消耗
动态开点实现的线段树1
code
struct node{
int ls,rs,sum,tag;
}tr[N];
int n,m,cnt=1;//一定要赋值成1
inline void push_up(int k){
tr[k].sum=tr[tr[k].ls].sum+tr[tr[k].rs].sum;
}
inline void push_down(int k,int l,int r){
if(tr[k].tag){
if(!tr[k].ls)tr[k].ls=++cnt;
if(!tr[k].rs)tr[k].rs=++cnt;
tr[tr[k].ls].tag+=tr[k].tag;
tr[tr[k].rs].tag+=tr[k].tag;
int mid=(l+r)>>1;
tr[tr[k].ls].sum+=(mid-l+1)*tr[k].tag;
tr[tr[k].rs].sum+=(r-mid)*tr[k].tag;
tr[k].tag=0;
}
}
inline void change(int &k,int l,int r,int x,int y,int val){
if(!k)k=++cnt;
if(x<=l&&r<=y) {
tr[k].tag+=val;
tr[k].sum+=val*(r-l+1);
return;
}
int mid=(l+r)>>1;
push_down(k,l,r);
if(x<=mid)change(tr[k].ls,l,mid,x,y,val);
if(y>mid)change(tr[k].rs,mid+1,r,x,y,val);
push_up(k);
}
inline int ask(int k,int l,int r,int x,int y){
if(!k)return 0;
if(x<=l&&y>=r)return tr[k].sum;
push_down(k,l,r);
int mid=(l+r)>>1,res=0;
if(x<=mid)res+=ask(tr[k].ls,l,mid,x,y);
if(y>mid)res+=ask(tr[k].rs,mid+1,r,x,y);
return res;
}
signed main(){
n=read();m=read();
int x;
up(i,1,n){
x=read();
int temp=1;
change(temp,1,n,i,i,x);
}
//cout<<tr[1].sum<<endl;
int op,l,r,t;
while(m--){
op=read();
if(op==1){
l=read();r=read();t=read();
int temp=1;
change(temp,1,n,l,r,t);
}
if(op==2){
l=read();r=read();
printf("%lld\n",ask(1,1,n,l,r));
}
}
return 0;
}
主席树
由前面的两种知识,如何转化成主席树。
主席树经典问题1:求区间第k大/小。
考虑建 $n$ 棵值域线段树,每棵值域线段树存储区间 $[1,i]$ 的信息,这样一来,要查询 $[l,r]$ 的第 $k$ 大时,只要在查询的过程中,将第$r$ 棵值域线段树的信息减去第 $l−1$ 棵值域线段树的信息即可,这利用了前缀和的思想。
但是建 $k$ 棵值域线段树,不论是时间还是空间,复杂度都是相当劣的。怎样优化呢?
3 5 8 6 7 2 1 4
建立值域线段树。
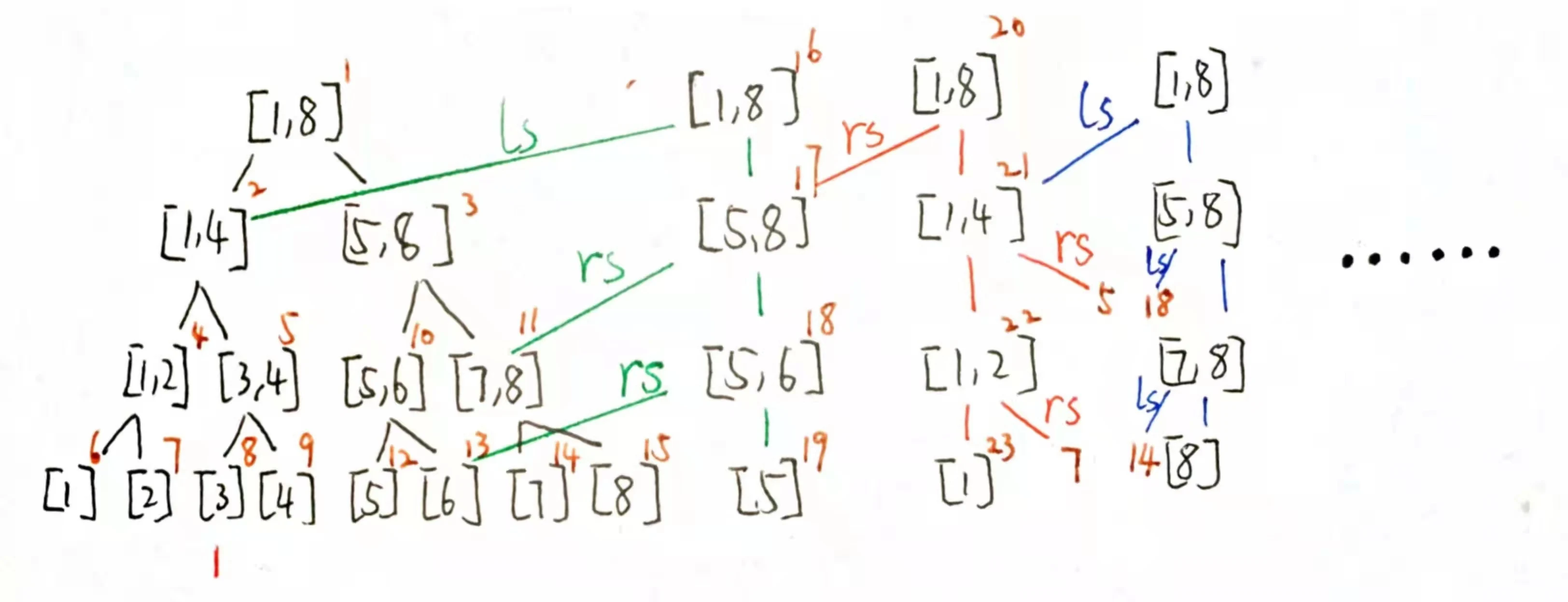
我们发现每次加入一个新的元素时更改的部分只会是一条链,而其他的部分则是无用的节点,自然的我们就想到能否让这两棵树共用这部分节点来减少节点的数量和建树的时间。
怎么操作呢?我们先建根结点,递归去看左孩子和右孩子,会发现左孩子的信息和上一棵树的是一样的,所以让他的左孩子直接指向上一棵树的左孩子,体现在代码中就是tr[k].ls=tr[last].ls
继续地递归且按照这种方式操作一直到叶子节点,这样我们就初步完成一颗最简单的主席树了。
当然,可持久化线段树难以支持大部分“区间修改”。
求区间第k大
[l,r]可以看做[1,r]-[1,l-1]。
两边双重递归,相减得出来的值就是答案。
code
int n,m;
int rt[N];
struct node{
int ls,rs,sum;
}tr[N<<5];
int a[N],cnt,b[N];
inline void build(int &k,int l,int r){
k=++cnt;
if(l==r){
tr[k].sum=a[l];
return;
}
int mid=(l+r)>>1;
build(tr[k].ls,l,mid);
build(tr[k].rs,mid+1,r);
}
inline void change(int &k,int pre,int l,int r,int x,int y){
k=++cnt;
tr[k]=tr[pre];tr[k].sum++;
if(l==r)return;
int mid=(l+r)>>1;
if(x<=mid)change(tr[k].ls,tr[pre].ls,l,mid,x,y);
if(y>mid)change(tr[k].rs,tr[pre].rs,mid+1,r,x,y);
}
inline int ask(int ll,int rr,int l,int r,int kth){
int x=tr[tr[rr].ls].sum-tr[tr[ll].ls].sum;
if(l==r) return b[l];
int mid=(l+r)>>1;
if(x>=kth) return ask(tr[ll].ls,tr[rr].ls,l,mid,kth);
return ask(tr[ll].rs,tr[rr].rs,mid+1,r,kth-x);
}
signed main(){
n=read();m=read();
up(i,1,n){
a[i]=read();
b[i]=a[i];
}
sort(b+1,b+1+n);
int maxl=unique(b+1,b+1+n)-b-1;
up(i,1,n){
int x=lower_bound(b+1,b+1+maxl,a[i])-b;
change(rt[i],rt[i-1],1,maxl,x,x);
}
int op,l,r,pre,x;
while(m--){
int l=read(),r=read(),k=read();
write(ask(rt[l-1],rt[r],1,maxl,k),1);
}
return 0;
}
可持久化线段树经典问题
可持久化线段树1
对区间历史进行修改,访问。
code
int n,m;
int rt[N];
struct node{
int ls,rs,sum,tag;
}tr[N<<5];
int a[N],cnt;
inline void build(int &k,int l,int r){
k=++cnt;
if(l==r){
tr[k].sum=a[l];
return;
}
int mid=(l+r)>>1;
build(tr[k].ls,l,mid);
build(tr[k].rs,mid+1,r);
}
inline void change(int &k,int pre,int l,int r,int x,int y,int val){
k=++cnt;
tr[k].ls=tr[pre].ls;tr[k].rs=tr[pre].rs;
tr[k].sum=tr[pre].sum;
if(l==r){
tr[k].sum=val;
return;
}
int mid=(l+r)>>1;
if(x<=mid)change(tr[k].ls,tr[pre].ls,l,mid,x,y,val);
if(y>mid)change(tr[k].rs,tr[pre].rs,mid+1,r,x,y,val);
}
inline int ask(int k,int l,int r,int x,int y){
if(l==r)return tr[k].sum;
int mid=(l+r)>>1;
if(mid>=x)return ask(tr[k].ls,l,mid,x,y);
else return ask(tr[k].rs,mid+1,r,x,y);
}
signed main(){
n=read();m=read();
up(i,1,n)a[i]=read();
build(rt[0],1,n);
int op,l,r,pre,x;
up(i,1,m){
pre=read();op=read();
if(op==1){
l=read();x=read();
change(rt[i],rt[pre],1,n,l,l,x);
}
if(op==2){
l=read();
write(ask(rt[pre],1,n,l,l),1);
rt[i]=rt[pre];
}
}
return 0;
}
询问区间某种颜色数量(可修)
struct node{
int l,r,sum;
}tr[N<<6];
int cnt,n,m,a[N],rk[N];
inline void push_up(int p){
tr[p].sum=tr[tr[p].l].sum+tr[tr[p].r].sum;
}
inline void update(int &p,int k,int l,int r,int val){
if(!p) p=++cnt;
if(l==r){
tr[p].sum+=val;
return ;
}
int mid=(l+r)>>1;
if(k<=mid) update(tr[p].l,k,l,mid,val);
else update(tr[p].r,k,mid+1,r,val);
push_up(p);
}
inline int ask(int p,int l,int r,int x,int y){
if(!p) return 0;
if(x<=l&&r<=y)return tr[p].sum;
int mid=(l+r)>>1,ans=0;
if(x<=mid) ans+=ask(tr[p].l,l,mid,x,y);
if(mid<y) ans+=ask(tr[p].r,mid+1,r,x,y);
return ans;
}
signed main(){
n=read();m=read();
up(i,1,n){
a[i]=read();
update(rk[a[i]],i,1,n,1);
}
while(m--){
int op=read(),l,r,x;
if(op==1){
l=read(),r=read(),x=read();
int ans=ask(rk[x],1,n,l,r);
printf("%d\n",ans);
}
else{
x=read();
update(rk[a[x]],x,1,n,-1);
update(rk[a[x+1]],x+1,1,n,-1);
update(rk[a[x]],x+1,1,n,1);
update(rk[a[x+1]],x,1,n,1);
int t=a[x];
a[x]=a[x+1];
a[x+1]=t;
}
}
return 0;
}
询问静态区间不同数的数量
这种问题一般是用莫队来解决,不过如果强制在线的话,就必须要用主席树或者是树套树,树套树支持动态修改但是比较慢,如果是静态区间可以用主席树。
如何用主席树对这种东西进行维护?
令tr[k].sum 表示 $k$ 所代表的区间的答案。
我们记录一个 $last$ 表示该数上一次出现是在那里。
如果这是第一次出现,当前版本答案加一,否则,新建一个版本为减去前一次出现的版本,再把当前版本加一。
int n,m;
int a[N],lst[N],pos[N];
int rt[N];
struct node{
int ls,rs,sum;
}tr[N<<5];
int cnt;
inline void change(int&k,int pre,int p,int val,int l,int r){
k=++cnt;
tr[k]=tr[pre];
tr[k].sum+=val;
if(l==r)return;
int mid=(l+r)>>1;
if(p<=mid)change(tr[k].ls,tr[pre].ls,p,val,l,mid);
else change(tr[k].rs,tr[pre].rs,p,val,mid+1,r);
}
inline int ask(int idx,int k,int l,int r) {
if(l==r)return tr[k].sum;
int mid=(l+r)>>1;
if (idx<=mid) return ask(idx,tr[k].ls,l,mid)+tr[tr[k].rs].sum;
else return ask(idx,tr[k].rs,mid+1,r);
}
signed main(){
n=read();
up(i,1,n){
a[i]=read();
if(lst[a[i]]==0){
change(rt[i],rt[i-1],i,1,1,n);
}
else{
int x;
change(x,rt[i-1],lst[a[i]],-1,1,n);
change(rt[i],x,i,1,1,n);
}
lst[a[i]]=i;
}
m=read();
int l,r;
while(m--){
l=read();r=read();
write(ask(l,rt[r],1,n),1);
}
return 0;
}