首先介绍图像退化、复原的一个线性模型,之后介绍噪声模型,接下来包含空间域滤波降噪和频率域降噪,介绍图像退化的线性和位置不变模型、估计退化函数的方法和基本的图像复原方法。
图像退化/复原过程的模型
目的:给定\(f(x,y)\)为输入图像,退化后的图像为\(g(x,y)\),退化函数为\(H\),加性噪声项为\(\eta(x,y)\),得到原始图像的一个估计\(\hat{f}(x,y)\),并且希望这个估计\(\hat{f}(x,y)\)尽可能的接近原始图像\(f(x,y)\)
空间域的退化图像如下表示:
其中\(h(x,y)\)是退化函数的空间表示,可以写成相应的频率域表示:
\[G(u,v) = H(u,v)F(u,v) + N(x,y) \]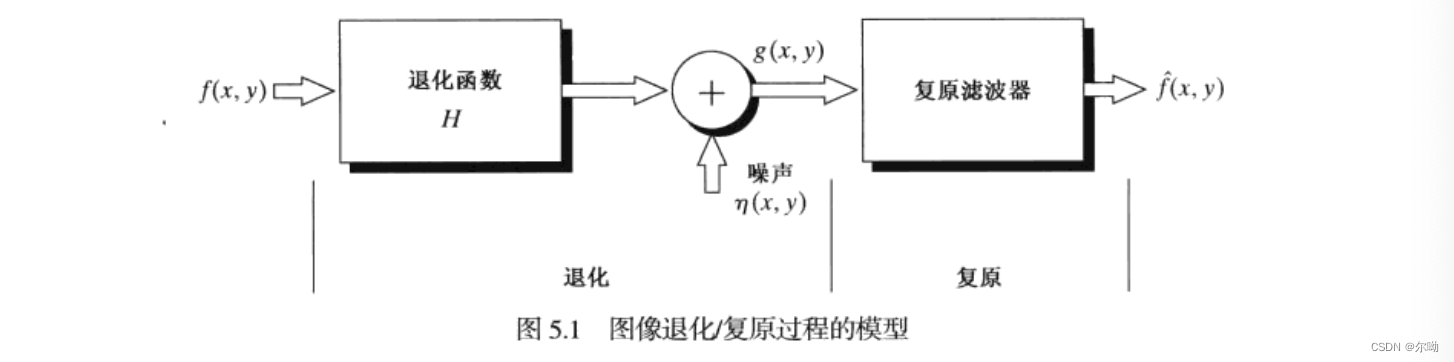
噪声模型
噪声主要产生于图像的获取和传输过程
一些重要的噪声概率密度函数
空间噪声描述子是噪声分量中灰度值的统计特性,可以看做是由概率密度函数PDF表征的随机变量,下图是一些重要的概率密度函数:
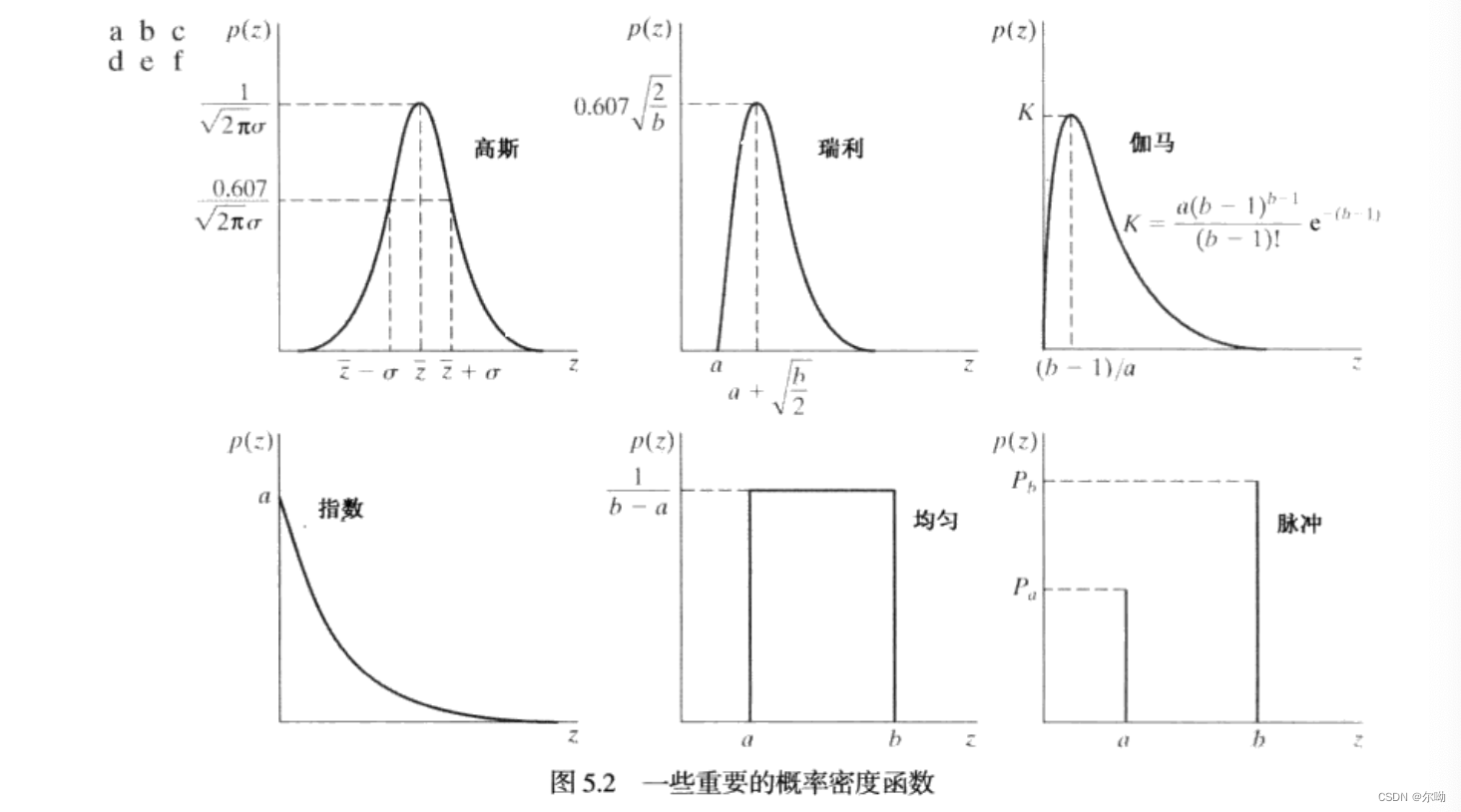
- 高斯噪声(正态噪声)
其中\(\overline{z}\)是\(z\)的平均值,\(\sigma\)是标准差
- 瑞利噪声
概率密度的均值和方差:
\[\overline{z} = a + \sqrt{\pi b/4} \\ \sigma^2 = \frac{b(4 - \pi)}{4} \]- 爱尔兰(伽马)噪声
概率密度的均值和方差:
\[\overline{z} = \frac{b}{a} \\ \sigma^2 = \frac{b}{a^2} \]- 指数噪声
概率密度的均值和方差:
\[\overline{z} = \frac{1}{a} \\ \sigma^2 = \frac{1}{a^2} \]- 均匀噪声
概率密度的均值和方差:
\[\overline{z} = \frac{a + b}{2} \\ \sigma^2 = \frac{(b - a)^2}{12} \]- 脉冲(椒盐)噪声
周期噪声
是在图像获取时由电力或机电干扰产生的,是空间相关噪声,可以通过频率域滤波来显著的减小
噪声参数的估计
周期噪声的参数通过计算图像的傅里叶谱来得到,噪声PDF的参数一般可以从传感器的技术说明中得知,但是有时参数需要估计,我们可以从图像中取一个小条带,也就是子图\(S,p_S(z_i),i = 0, 1, 2, \cdots, L - 1\)表示条带中像素的概率估计,也就是直方图,之后计算该条带的均值和方差:
\[\overline{z} = \sum_{i = 0}^{L - 1}z_ip_s(z_i) \\ \sigma^2 = \sum_{i = 0}^{L - 1}(z_i - \overline{z})^2 p_s(z_i) \]只存在噪声的复原-空间滤波
当图像中存在的唯一退化是噪声的时候,模型变为:
\[g(x,y) = f(x,y) + \eta(x,y) \\ G(u,v) = F(u,v) + N(u,v) \]在周期噪声的情况下,\(N(u,v)\)可以估计出来,但是一般情况下不能直接计算出来,当仅存在加性噪声的情况下,可以选择空间滤波
均值滤波器
算术均值滤波器和几何均值滤波器更适合于处理高斯或均匀随机噪声,逆谐波均值滤波器更适合于处理脉冲噪声,但是必须要知道是暗噪声还是亮噪声以便选择\(Q\)值
- 算数均值滤波器,令\(S_{xy}\)表示中心在\((x,y)\)处,大小为\(m \times n\)的矩形子图像窗口的一组坐标,算数均值滤波器在这个区域内计算被污染图像\(g(x,y)\)的均值
- 几何均值滤波器,丢失了更少的细节
- 谐波均值滤波器,善于处理盐粒噪声,但不适用于胡椒噪声
- 逆谐波均值滤波器,\(Q\)称为滤波器的阶数,当\(Q\)为正时消除胡椒噪声,为负时消除盐粒噪声,但是不能同时消除两种噪声,可以看到当\(Q = 0\)的时候就是算数均值滤波器,当\(Q = -1\)时是谐波均值滤波器
统计排序滤波器
- 中值滤波器,对存在单级或双极脉冲噪声尤其有效
- 最大值和最小值滤波器,分别降低胡椒噪声和盐粒噪声
- 中点滤波器,对随机分布噪声如高斯噪声和均匀噪声很好
- 修正的阿尔法均值滤波器,在邻域\(S_{xy}\)内去掉最低灰度值的\(\frac{d}{2}\)和最高灰度值的\(\frac{d}{2}\),令\(g_r(s,t)\)表示剩下的\(mn - d\)个像素
自适应滤波器
- 自适应局部降低噪声滤波器,有邻域\(S_{xy}\),滤波器在邻域中心\((x,y)\)的响应基于以下几个量,\(g(x,y)\)表示带噪图像上的量,\(\sigma_\eta^2\)表示污染图像\(f(x,y)\)以形成\(g(x,y)\)的噪声的方差,这个值需要估计,\(m_L\)表示\(S_{xy}\)中像素的均值,\(\sigma_L^2\)表示\(S_{xy}\)中像素的局部方差
如果两个方差比值为1那么返回的是邻域中像素的平均值,假如\(\sigma_\eta^2 = 0\)也就是没有噪声,返回的是\(g(x,y)\)
- 自适应中值滤波器,中值滤波器在脉冲噪声的空间密度不大(\(P_a<0.2,P_b<0.2\))的时候性能很好,自适应中值滤波可以处理更大概率的脉冲噪声,\(z_{min}\)表示\(S_{xy}\)中的最小灰度值,\(z_{max}\)表示\(S_{xy}\)中的最大灰度值,\(z_{med}\)表示\(S_{xy}\)中的灰度值的中值,\(z_{xy}\)表示\(S_{xy}\)中坐标\((x,y)\)的灰度值,\(S_{max}\)表示\(S_{xy}\)的最大尺寸
进程A:
进程B:
\[\begin{aligned} &B_1 = z_{xy} - z_{min} \\ &B_2 = z_{xy} - z_{max} \\ &如果B_1 > 0,B_2 < 0那么输出z_{xy} \\ &否则输出z_{med} \end{aligned} \]用频率域滤波消除周期噪声
用频率域计数可以有效的分析并滤除周期噪声,其基本概念是在傅里叶变换中,周期噪声在对应于周期干扰的频率处,以集中的能量脉冲形式出现,可以使用带阻(分离图像)、带通(分离噪声)和陷波滤波器滤除
最佳陷波滤波
干扰噪声模式的傅里叶变换可以通过陷波带通滤波器\(H_{NP}(u,v)\)得到
\[N(u,v) = H_{NP}(u,v)G(u,v) \]由此可以得到干扰噪声模式:
\[\eta(x,y) = \mathfrak{J}^{-1}\{H_{NP}(u,v)G(u,v)\} \]当被污染图像是由原图像\(f(x,y)\)和噪声\(\eta(x,y)\)相加得到,那么可以得到原图像的近似值:
\[\hat{f}(x,y) = g(x,y) - w(x,y)\eta(x,y) \]\(w(x,y)\)称为加权函数或调制函数,需要选择,一种方法是选取\(w(x,y)\)使得估计值\(\hat{f}(x,y)\)在每一点\((x,y)\)的指定邻域上的方差最小,考虑大小为\((2a + 1)(2b + 1)\)的邻域,\(\hat{f}(x,y)\)的局部方差:
\[\sigma^2(x,y) = \frac{1}{(2a + 1)(2b + 1)}\sum_{s = -a}^a\sum_{t = -b}^b\left[\hat{f}(x + s,y + t) - \overline{\hat{f}}(x,y)\right] \]其中\(\overline{\hat{f}}(x,y)\)是该领域内\(\hat{f}\)的平均值:
\[\overline{\hat{f}}(x,y) = \frac{1}{(2a+1)(2b+1)}\sum_{s = -a}^a\sum_{t = -b}^b\hat{f}(x + s,y + t) \]综合上式得到:
\[\sigma^2(x,y) = \frac{1}{(2a + 1)(2b + 1)}\sum_{s = -a}^a\sum_{t = -b}^b\{[g(x+s,y+t) - w(x+s,y+t)\eta(x+s,y+t)] - [\overline{g}(x,y) - \overline{w(x,y)\eta(x,y)]}\}^2 \]假设\(w(x,y)\)在整个邻域内保持不变,那么当\(-a \leq s \leq a,-b \leq t \leq b\):
\[w(x + s, y + t) = w(x,y) \]有:
\[\sigma^2(x,y) = \frac{1}{(2a + 1)(2b + 1)}\sum_{s = -a}^a\sum_{t = -b}^b\{[g(x+s,y+t) - w(x+s,y+t)\eta(x+s,y+t)] - [\overline{g}(x,y) - w(x,y)\overline{\eta}(x,y)]\}^2 \]求的是\(\sigma^2(x,y)\)的最小值,对上式求导:
\[w(x,y) = \frac{\overline{g(x,y)\eta(x,y)} - \overline{g}(x,y)\overline{\eta}(x,y)}{\overline{\eta^2}(x,y) - \overline{\eta}^2(x,y)} \]线性、位置不变的退化
系统\(H\)满足加性和均匀性,则是一个线性系统:
- 加性:
- 均匀性:
位置不变系统:图像中任意一点处的响应只取决于该点处的输入值,与该点的位置无关
\[H[f(x - \alpha,y - \beta)] = g(x - \alpha,y - \beta) \]现在有式子:
\[f(x,y) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(\alpha,\beta)\delta(x - \alpha,y - \beta)d\alpha d\beta \]暂且假设\(\eta(x,y) = 0\),有
\[g(x,y) = H[(f(x,y)] = H\left[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(\alpha,\beta)\delta(x - \alpha,y - \beta)d\alpha d\beta\right] \]假设\(H\)是线性算子,将加性性质扩展到积分
\[g(x,y) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}H\left[f(\alpha,\beta)\delta(x - \alpha,y - \beta)\right]d\alpha d\beta \]使用均匀性可以得到
\[g(x,y) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(\alpha,\beta)H\left[\delta(x - \alpha,y - \beta)\right]d\alpha d\beta \]系统\(H\)的冲激响应如下:通常称为点扩散函数
\[h(x,\alpha,y,\beta) = H[\delta(x - \alpha,y - \beta)] \]得到:
\[g(x,y) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(\alpha,\beta)h(x,\alpha,y,\beta)d\alpha d\beta \]上式称为第一类叠加(弗雷德霍姆)积分,这个表达式是线性系统理论核心中的一个基础结果,它表明,如果系统\(H\)对一个冲激的响应已知,则对任意输入\(f(\alpha,\beta)\)的响应可以用上式来计算,假设\(H\)是位置不变的,那么
\[H[\delta(x - \alpha,y - \beta)] = h(x - \alpha,y - \beta) \]在这种情况下,考虑加性噪声,退化模型的表达式变为:
\[g(x,y) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(\alpha,\beta)h(x-\alpha,y-\beta)d\alpha d\beta + \eta(x,y) \]噪声项是随机的,假设和位置无关,那么可以将退化模型表示为:
\[g(x,y) = h(x,y)★f(x,y) + \eta(x,y) \]在频率域中:
\[G(u,v) = H(u,v)F(u,v) + N(u,v) \]具有加性噪声的线性空间不变退化系统,可以在空间域建模为退化(点扩散)函数与一幅图像的卷积,然后再加上噪声,许多类型的退化可以近似为线性、位置不变的过程,于是可以使用线性系统的理论工具来解决图像复原问题,术语去卷积常用于表示线性图像复原,用于复原处理的滤波器常称为去卷积滤波器
标签:infty,frac,05,噪声,图像复原,beta,图像处理,alpha,滤波器 From: https://www.cnblogs.com/eryoyo/p/16758234.html