ABC209E Shiritori 题解
分析
博弈,可重复选,一眼图论,将每个单词的前三个字符向后三个字符连边,并用后三个字符代表这个单词。
看一下样例。
5
eaaaabaa
1 2
eaaaacaa
1 3
daaaaaaa
4 5
eaaaadaa
1 4
daaaafaa
4 6
我们得到的有向图:
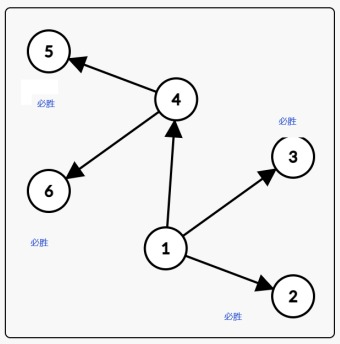
当一方说完一个单词,这个单词的后三个字符无法接上任何单词的前三个字符则为必胜态。
即这个点没有出边,则这个点是必胜态。
注意,本题博弈的状态转移有些不同,具体为:
当一个点连向的点中有一个必胜态,则这个点是必败态。
当一个点连向的点都是必败态,则这个点是必胜态。
常见的状态转移:
当一个点连向的点中有一个必败态,则这个点是必胜态
当一个点连向的点都是必胜态,则这个点是必败态
分析一下,一方走到这个点之后,下一手是对方,也就是说对方决定了下一次要走哪条边。
那么对方肯定是想让当前点成为必败态,想要尽可能走到必胜态。所以就有了本题稍为不同的状态转移。
另两篇没有注意到这一点,文字叙述中说的是常见的状态转移或是笼统模糊地说了说,但代码实现却是对的,卡了我很长时间(
具体可以以 \(\large1\) 号点为例(虽然 \(\large1\) 号点在样例中并无实际意义,我们假定它也代表了一个单词):
首先 \(\large4\) 号点一定是必败态,因为 \(\large 5\) 和 \(\large 6\) 都是必胜态。
那么当一方说完 \(\large 1\) 号点代表的单词后,该对方接了,对方肯定会接 \(\large 2\) 或 \(\large 3\) 而不接 \(\large 4\)。因为只有走到这两点,才能使当前点败,他胜。
套路
我们观察到,所有有出边的点的状态都是由它连向的点(后继)转移而来的,所以我们使用有向图上博弈的常见套路——反向建边。然后跑拓扑同时状态转移就可以了。
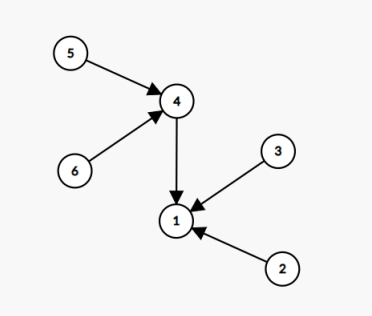
到此,\(\operatorname{DAG}\) 上的本题就已经讨论完了,但是我们还没有判平局,即有环的情况。
平局(环)
有环是不一定平局的,分析一下。
(正向图中)在一个环里,一方说完了一个单词,如果对方可以走到必胜态,肯定会走处环使得自己胜而不是平局。但是如果这个环没有向外连边或连向的都是必败态,那么就是平局。
那么在反向图中,我们在遍历一个必胜的点的出边时,不必在后继的入度为零时才让它入队,直接把它的状态转移为必败并入队。若是遍历一个必败的点的出边,正常拓扑即可。
code
#include<bits/stdc++.h>
#define int long long
#define reg register
#define mp(a,b) make_pair((a),(b))
using namespace std;
inline int read()
{
short f=1;
char c=getchar();
int x=0;
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(int)(c^48),c=getchar();
return x*f;
}
int n,tot,ind[200010],win[200010]/*0平/未查找 1败 2胜*/;
string l,r[200010],s,ans[3]={"Draw","Aoki","Takahashi"};//不想写if了qwq
unordered_map<string,int>c;
vector<int>e[200010];
queue<int>q;
signed main()
{
n=read();
for(reg int i=1;i<=n;i=-~i)
{
cin>>s;l="";
for(reg int j=0;j<3;j=-~j) l+=s[j];
for(reg int j=s.size()-3;j<(int)s.size();j=-~j) r[i]+=s[j];
if(!c[l]) c[l]=++tot;//没必要哈希,用map编号即可
if(!c[r[i]]) c[r[i]]=++tot;
e[c[r[i]]].push_back(c[l])/*反向建边*/;ind[c[l]]=-~ind[c[l]];
}
for(reg int i=1;i<=tot;i=-~i) if(!ind[i]) q.push(i),win[i]=2;
while(!q.empty())
{
int u=q.front();q.pop();
for(reg auto i:e[u])
{
if(!win[i]&&win[u]==2) q.push(i),win[i]=1;
if(!win[i]&&win[u]==1&&!--ind[i]) q.push(i),win[i]=2;
}
}
for(reg int i=1;i<=n;i=-~i) cout<<ans[win[c[r[i]]]]<<endl;
return 0;
}