3D游戏开发中的数学知识矩阵详解

矩阵很多同学没有接触过，所以感觉很难，很复杂，其实只要学过矩阵的同学都知道，矩阵运算并不难。今天我们给大家讲讲游戏开发中的矩阵的运算。

1:矩阵是什么?

矩阵是描述线性变换的一种数学工具,线性变换指的是使用一次函数从一个空间变换到另外一个空间。

例如在空间A中的一个2维向量（xa, ya）变换到空间B，使用一次线性函数变换后得(xb, yb)。

xb = A*xa + B*ya + C;

yb = M*xa + N*ya + D;

 对啦！这里有个游戏开发交流小组里面聚集了一帮热爱学习游戏的零基础小白，也有一些正在从事游戏开发的技术大佬，欢迎你来交流学习。

上述变换中，xb 是由xa, ya 经过线性运算而得到得。如果xb = A*xa^2 + B*ya + C,这样就不是线性变换了。

数学前辈们为了描述上面的线性变换，发明了矩阵,把上面的变换标记为:

上面的变换，(xa, ya)通过矩阵变换到(xb, yb),用矩阵是如何变换的呢？我们实际就是把(xa, ya)*矩阵 = (xb, yb)。

2: 向量与矩阵, 矩阵与矩阵的乘法;

向量与矩阵乘法:

按照上述的例子我们一起来计算一下，空间Va的向量(xa, ya), 变换到空间Vb的向量(xb, yb)

(1): 扩展向量的维度为3维, (xa, ya)变成了(xa, ya, 1)

(2): 计算(xa, ya, 1) * 矩阵

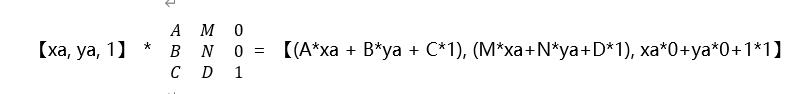
总结一下向量与矩阵的乘法规则:

新向量的第i个元素，等于原来向量的每个元素与第i列矩阵的每个对应数据相乘后相加。由这个规则，我们可以得到向量与矩阵相乘向量的维度必须和矩阵的行数一样。

很多同学马上就会有疑问了，矩阵既然最后还是要结合元素计算，我干嘛还要用矩阵呢？直接算不就可以么？接下来矩阵得第二个妙处就在于每个线性变化都对应一个矩阵，我们可以把多次线性变换叠加起来，这样就可以减少运算的次数。比如我要把100个点，由V1空间，变换到v2空间，再变换到v3空间。V1到v2对应一个矩阵，v2到v3对应一个矩阵，我们可以把这两个矩阵变换叠加起来变成一个矩阵。100个点，每个点计算一次矩阵乘法即可得到新的点，而不用每个点计算2次矩阵乘法得到新的点。

如何把多个矩阵对应的多次线性变换叠加起来呢？这个就是矩阵与矩阵的乘法。例如

根据上面的规律，新矩阵的对应第i行第j列元素，我们叫做元素ij。矩阵变化的叠加就是矩阵乘法，矩阵乘法的计算规则如下：

A矩阵*B矩阵=C矩阵, Cij = Ai0*Bj0 + Ai1*Bj1 + ….. ;即Cij为A的第i行与B的第j列的每项数据相乘后的和(即dot(Ai, Bj))。根据上面的规则，我们发现两个矩阵要能相乘必须要满足一个条件，就是左边矩阵的列数等于右边矩阵的行数,否者两个矩阵是无法相乘的。

3: 游戏开发中的缩放，旋转平移矩阵;

游戏开发中常用的线性变换有缩放，平移, 旋转, 这个我们通常叫做transform。而这些变换叠加在一起，就是我们在游戏世界中摆放游戏物体，我们可以把每个物体的线性变换，叠加在一起，形成一个矩阵，然后我们再来做坐标变换。

先来看平移矩阵，我们以2D为例, 向量(x, y)平移变换到新的空间,平移就是把x, y都加上一个常量。那么平移变换矩阵为

缩放矩阵: 向量(x, y)通过缩放，到新的空间

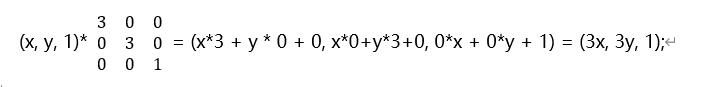
我们叠加在一起运算一下, 先缩放还是先平移，得到的结果不一样，先平移后缩放的结果是 (x, y, 1) 先平移dx, dy, 后缩放3倍，(3x+3*dx, 3y + 3*dy, 1), 先缩放后平移, 得到的结果是(3x+dx, 3y + dy, 1)。

我们反应到矩阵，先平移后缩放，平移矩阵*缩放矩阵，如下:

同理，如果是先缩放后平移，缩放矩阵*平移矩阵，如下:

同样是两个矩阵，乘法的位置不一样，得到的结果可能不一样。

4: 3D游戏中的旋转矩阵，单位矩阵, 逆矩阵;

平移缩放，大家都好理解了，旋转矩阵不那么直观，特别是3D的。我们以大家熟悉的欧拉旋转为例。

比如我们在3D里面先绕x轴旋转 a度，再绕y轴旋转b度，再绕z轴旋转c度。这个其实就是3个空间的变换，每次变换，都对应一个旋转矩阵，然后我们按照顺序把这三个矩阵叠加起来 Rx * Ry * Rz = R旋转。根据我们上面的分析，矩阵的位置不一样，得到的结果会不一样，所以每个游戏引擎的欧拉角旋转都会有一个固定的顺序来计算, 最终就得到一个旋转矩阵。

最后说几个比较特殊的矩阵，单位矩阵，就是乘以这个矩阵后不会发生任何改变，相当于没有变化。

逆矩阵: 矩阵A的反向矩阵叫A的逆矩阵即: A矩阵*A的逆矩阵=单位矩阵, 两个互为逆矩阵的叠加在一起，相当于没有变化。

今天的矩阵就讲解到这里，关注我, 在我们公开课中可以免费获得矩阵的视频讲解的课程。