问题大意:
从围成标有记号 \(1\) 到 \(n\) 个人开始,每隔一个删去一个人,直到最后只有一个人幸存下来。例如 \(n=10\) 的起始图形:
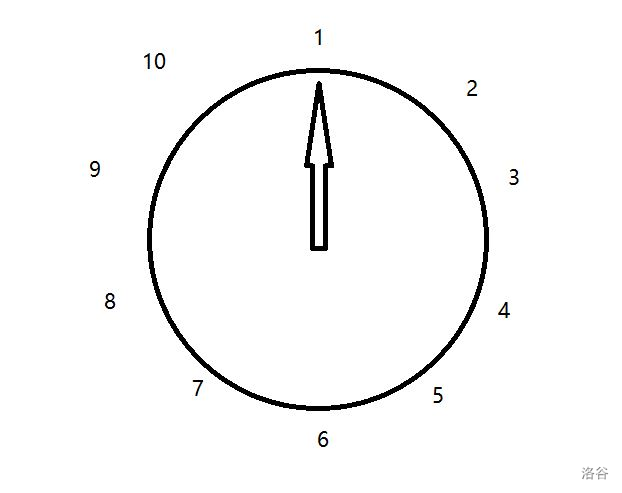
删除的顺序是:\(2,4,6,8,10,3,7,1,9\) ,最后 \(5\) 幸存下来。
解决:
我们设对于有 \(n\) 个人的环,最终幸存者编号为 \(F_n\)。
所以 \(F_{10}=5\)。接着我们模拟几个小的情况,可以打出如下的表。
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
|---|---|---|---|---|---|---|
| \(F_{n}\) | \(1\) | \(1\) | \(3\) | \(1\) | \(3\) | \(5\) |
这看起来感觉 \(F_n\) 总是奇数,仔细一想会发现绕完一圈后所有的偶数都被删除了,这样似乎人数就会减半。
所以我们分奇偶性来考虑这个问题。
对于偶数的情形,假设一开始有 \(2n\) 个人,经过第一轮后剩下的是:
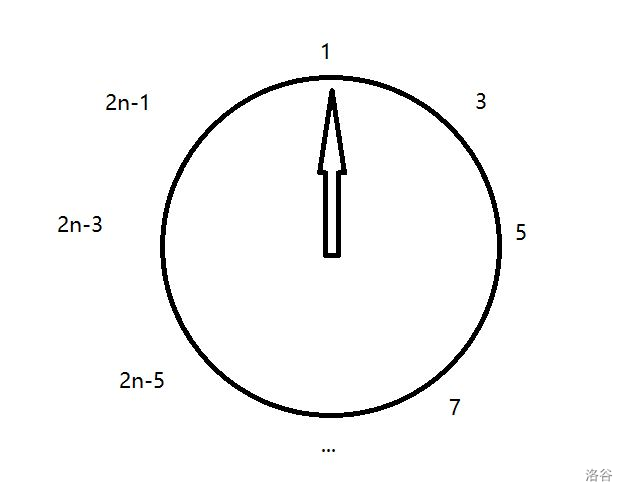
\(3\) 号就是下一个被删除的人,仔细一点会发现,除了每个人的编号加倍并减一之外,此时的情形正对应着 \(n\) 个人开始时的情形,就是说:
\(F_{2n}=2F_{n}-1\),\(n≥1\)。
对于奇数的情形,假设一开始有 \(2n+1\) 个人,经过第一轮后剩下的是:
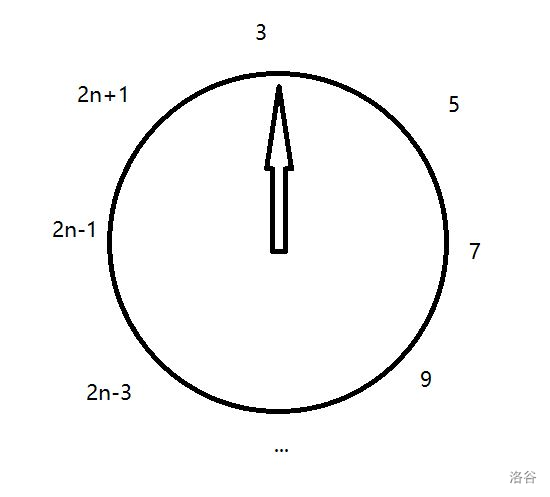
我们再次得到与 \(n\) 个人开始时相似的情形,但这一次他们的编号加倍并加一,就是说:
\(F_{2n+1}=2F_{n}+1\),\(n≥1\)。
我们把这些结合起来:
得到关于 \(F\) 的递推式:
\(F_1=1\);
\(F_{2n}=2F_{n}-1\),\(n≥1\);----------\((1.1)\)
\(F_{2n+1}=2F_{n}+1\),\(n≥1\)。
有了递推式,我们来寻找它的封闭形式,因为封闭形式算得会更快,同时也会蕴含更丰富的信息。
我们通过得到的递推式来打一张表:
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) | \(10\) | \(11\) | \(12\) | \(13\) | \(14\) | \(15\) | \(16\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(F_n\) | \(1\) | \(1\) | \(3\) | \(1\) | \(3\) | \(5\) | \(7\) | \(1\) | \(3\) | \(5\) | \(7\) | \(9\) | \(11\) | \(13\) | \(17\) | \(1\) |
我们似乎找到了它的规律,可以按照 \(2\) 的幂将表中的数据分组。每一组的开始\(F_n\)总等于 \(1\),并且组里的数据每次递增 \(2\)。因此,如果我们把 \(n\) 写成 \(2^m+1\) 的形式,其中 \(2^m\) 是不超过 \(n\) 的 \(2\) 的最大幂,\(l\)则是剩下的数,那么递推式的解看起来是:
\(F_{2^m+ l}=2l+1\),\(m≥0\),\(0≤l≤2^m\)。----------\((1.2)\)
注意,如果 \(2^m≤n<2^{m+1}\),则余下来的数 \(l=n-2^m\) 满足 \(0≤l<2^{m+1}-2^m=2^m\)。
接下来我们考虑证明这个式子,我们对 \(m\) 用归纳法,当 \(m=0\) 时必有 \(l=0\),于是式 \((1.2)\) 的基础就是 \(F_1=1\),此结论为真。接着分奇偶性来归纳证明。
如果 \(m>0\) 且 \(2^m+l=2n\),则 \(l\) 定是偶数,根据式 \((1.1)\) 和归纳假设,有:
\(F_{2^m+l}=2F_{2^{m-1}+l/2}-1=2(2l/2+1)-1=2l+1\)。
如果 \(2^m+l=2n+1\),则 \(l\) 定是奇数,有:
\(F_{2^m+l}=2F_{2^{m-1}+( l-1)/2}+1=2(2(l-1)/2+1)+1=2l+1\)。
得证式 \((1.2)\)。
到此为止,我们解决了问题。
该问题补充
接下来我们探讨式 \((1.1)\) 和式 \((1.2)\) 的某些推广,揭示这背后的隐藏结构。
在我们求解的过程中,\(2\) 的幂起着重要的作用,所以自然来研究 \(n\) 与 \(F_n\) 的以 \(2\) 为基数的表示,把 \(n\) 用二进制来表示:
\(n=(b_mb_{m-1}...b_1b_0)_2\)
也就是说,\(n=b_m2^m+b_{m-1}2^{m-1}+...+b_12^1+b_02^0\)
其中 \(b_i\) 为 \(0\) 或 \(1\),而首位数字 \(b_m\)是 \(1\),注意 \(n=2^m+l\),于是我们依次就有:
\(n=(1b_{m-1}b_{m-2}...b_1b_0)_2\);
\(l=(0b_{m-1}b_{m-2}...b_1b_0)_2\);
\(2l=(b_{m-1}b_{m-2}...b_1b_00)_2\);
\(2l+1=(b_{m-1}b_{m-2}...b_1b_01)_2\);
\(F_n=(b_{m-1}b_{m-2}...b_1b_01)_2\);
因为 \(b_m=1\),又有 \(F_n=(b_{m-1}b_{m-2}...b_1b_0b_m)_2\)。
我们就证明出:
\(F_{(b_mb_{m-1}...b_1b_0)_2}=(b_{m-1}...b_1b_0b_m)_2\)
用计算机程序设计的行话来说就是,\(n\) 向左循环移动一位就得到 \(F_n\),这样的表达是不是比刚才的好理解多了?
\(plus\)
好的,我们已经非常了解函数 \(F\) 了,接下来我们对它加以推广,如果我们的问题产生了与式 \((1.1)\) 有些相像的递推式(不过有不同的常数),将会发生什么呢?我们引入常数 \(x,y,z\),则有
\(f_1=x\);
\(f_{2n}=2f_n+y\);----------\((1.3)\)
\(f_{2n+1}=2f_n+z\);
接下来我们力图对更加一般的递归式(1.3)求出一个封闭形式。
(原来的递归式中有 \(x=1,y=-1,z=1\))从 \(f_1=x\) 出发并按照我们的思路做下去,可以对小的 \(n\) 值构造出如下一般性的表:
| \(n\) | \(f_n\) |
|---|---|
| \(1\) | \(x\) |
| \(2\) | \(2x+y\) |
| \(3\) | \(2x+z\) |
| \(4\) | \(4x+3y\) |
| \(5\) | \(4x+2y+z\) |
| \(6\) | \(4x+y+2z\) |
| \(7\) | \(4x+3z\) |
| \(8\) | \(8x+7y\) |
| \(9\) | \(8x+6y+z\) |
看起来 \(x\) 的系数是不超过 \(n\) 的 \(2\) 的最大幂,同时,在 \(2\) 的幂之间,\(y\) 的系数递减 \(1\) 直到 \(0\),\(z\) 的系数则从 \(0\) 开始递增 \(1\)。就类似于二项式定理的 \(a,b\) 的指数。于是,如果把 \(f_n\) 对 \(x,y,z\) 的依存关系分离开来,我们就把它表示成形式:
\(f_n=A_nx+B_ny+C_nz\)。----------\((1.4)\)
看起来有:
\(A_n=2^m\);
\(B_n=2^m-1-l\);----------\((1.5)\)
\(C_n=l\)
如通常一样,这里有 \(n=2^m+l\) 以及 \(0≤l<2^m\)(\(n≥1\))。
我们考虑用归纳法证明 \((1.4)\) 和 \((1.5)\),同样分成奇偶性来证明:
如果 \(m>0\) 且 \(2^m+l=2n\),则 \(l\) 定是偶数,则有:
\(f_{2m+l}=2f_{2^{m-1}+l/2}+y=2(2^{m-1}x+(2^{m-1}-1-l/2)y+(l/2)z)+y=2^mx+(2^m-1-l)y+lz\)。
如果 \(2^m+l=2n+1\),则 \(l\) 定是奇数,有:
\(f_{2^m+l}=2f_{2^{m-1}+(l-1)/2}+z=2(2^{m-1}x+(2^{m-1}-1-(l-1)/2)y+((l-1)/2)z)+z=2^mx+(2^m-1-l)y+lz\)。
会发现算出来的 \(x,y,z\) 的系数与式 \((1.5)\) 的相同,得证。
当然,还有一种巧妙的方法,可以通过选取特殊值,并将它们组合起来,本文不再展开讲述。
我们知道原来的约瑟夫问题有个奇妙的解,写成二进制是:
\(F_{(b_mb_{m-1}...b_1b_0)_2}=(b_{m-1}...b_1b_0b_m)_2\),(\(b^m=1\))。
推广的约瑟夫问题是否也有这样奇妙的解呢?
令 \(\beta_0=y,\beta_1=z\),那么我们可以把推广的递推式 \((1.3)\) 改写成:
\(f_1=x\);
\(f_{2n+j}=2f_n+\beta_j\),\(j=0,1\),\(n≥1\)。----------\((1.6)\)
这个递推式写成二进制就是:
\(f_{(b_mb_{m-1}...b_1b_0)_2}=2f_{(b_mb_{m-1}...b_1)_2}+\beta_{b_0}\)
继续递归会有:
\(=4f_{(b_mb_{m-1}...b_2)_2}+2\beta_{b_1}+\beta_{b_0}\)
\(=...=2^mf_{(b_m)_2}+2^{m-1}\beta_{b_{m-1}}+...+2\beta_{b_1}+\beta_{b_0}\)
\(=2^mx+2^{m-1}\beta_{b_{m-1}}+...+2\beta_{b_1}+\beta_{b_0}\)。
现在我们解除二进制表示,允许任意的数字,而不仅是数字 \(0\) 和 \(1\),那么上述的推导告诉我们:
\(f_{(b_mb_{m-1}...b_1b_0)_2}=(x\beta_{b_{m-1}}\beta_{b_{m-2}}...\beta_{b_1}\beta_{b_0})_2\)。----------(1.7)
这里比较抽象,实际上这个值是等于:
\(2^mx+2^{m-1}\beta_{b_{m-1}}+2^{m-2}\beta_{b_{m-2}}+...+2^{1}\beta_{b_{1}}+2^{0}\beta_{b_{0}}\)。
很好,如果把刚才的表:
| \(n\) | \(f_n\) |
|---|---|
| \(1\) | \(x\) |
| \(2\) | \(2x+y\) |
| \(3\) | \(2x+z\) |
| \(4\) | \(4x+3y\) |
| \(5\) | \(4x+2y+z\) |
| \(6\) | \(4x+y+2z\) |
| \(7\) | \(4x+3z\) |
| \(8\) | \(8x+7y\) |
| \(9\) | \(8x+6y+z\) |
用另一种方式写成:
| \(n\) | \(f_n\) |
|---|---|
| \(1\) | \(x\) |
| \(2\) | \(2x+y\) |
| \(3\) | \(2x+z\) |
| \(4\) | \(4x+2y+y\) |
| \(5\) | \(4x+2y+z\) |
| \(6\) | \(4x+y+2z\) |
| \(7\) | \(4x+2z+z\) |
| \(8\) | \(8x+4y+2y+y\) |
| \(9\) | \(8x+4y+2y+z\) |
我们就能更早看到这种规律,从而推出循环移位性质。
所以,改变表示法使得我们对于一般的递推式 \((1.6)\) 给出了紧凑的解 \((1.7)\)。
\(plus^2\)
如果真的不受限制,我们进一步加以推广,递推式:
\(f_j=x_j\),\(1≤j<d\);
\(f_{dn+j}=cf_n+\beta_j\),\(0≤j<d\),\(n≥1\)。
与上一个递推式是相同的,除了这里是从基数为 \(d\) 的数入手,而产生的值使用基数 \(c\) 表示之外,这就是说,它有变动基数的解:
\(f_{(b_mb_{m-1}...b_1b_0)_d}=(x_{b_m}\beta_{b_{m-1}}\beta_{b_{m-2}}...\beta_{b_1}\beta_{b_0})_c\)。
(想要理解到这里是非常困难的,必须深刻体会和领悟)
于是,约瑟夫把我们引向了某种有趣的一般递归式。
写作目的
一方面是为了作者自身更深刻地体和领悟会这些知识。
另一方面发现在内网很难找到有关这类问题的文章,可以让更多的人了解到这些知识。
标签:...,4x,约瑟夫,问题,beta,1b,深入,2n,递推 From: https://www.cnblogs.com/Exotic-sum/p/17753176.html