首页 > 其他分享 >笔记——线段树

笔记——线段树

时间：2023-10-04 22:34:32浏览次数：53  
标签：text 线段 mid 笔记 tag 区间 LL

蓝月の笔记——线段树篇

在树状数组中，我们讲解了关于单点修改区间查询的操作。今天，我们要讲一种更加高级的数据结构，他解决的是区间修改区间查询的问题多了一个区间当然更高级啦。

这个数据结构就是——线段树

Luogu - P3372

给定一个长度为 \(n\) 的序列 \(a_1,a_2,\cdots,a_n\) 和两种操作：

  1. 输入 1 l r k，将 \([l,r]\) 区间里的每一个数加上 \(x\)；
  2. 输入 2 l r，求 \(\sum_{i=l}^{r}a_i\)。

这就是区间修改区间查询。

正片开始

先看图

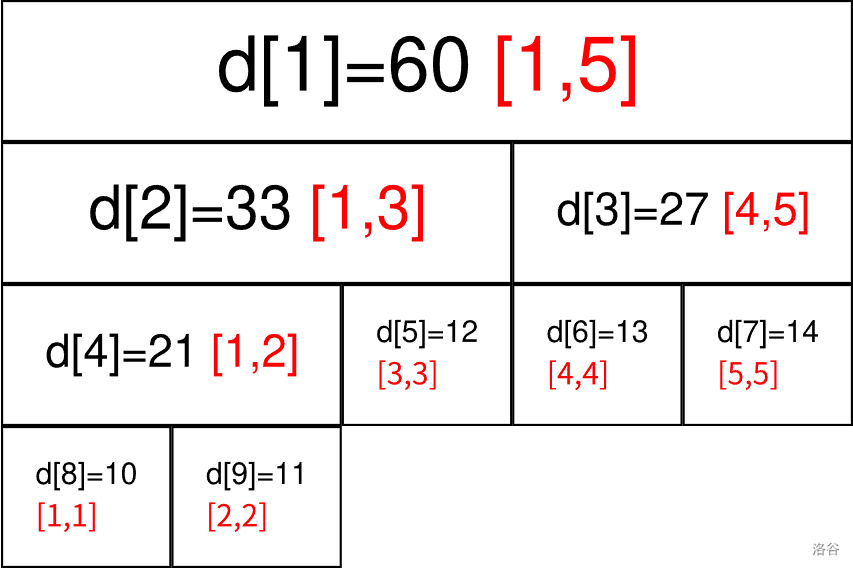
【图片来源：OI-Wiki】

这就是线段树的建出来的树。所以我们就讲完了（逃

注意：线段树是一颗二叉树

所以讲解函数之前，我们要了解二叉树的子节点查看方法。

观察图，我可以看出：\(1\) 的子节点是 \(2(1 \times 2)\) 和 \(3(1 \times 2 + 1)\)，\(2\) 的子节点是 \(4(2 \times 2)\) 和 \(5(2 \times 2 + 1)\)，\(3\) 的子节点是 \(6(3 \times 2)\) 和 \(7(3 \times 2 + 1)\)。

以此类推，我们知道：编号为 \(i\) 的非叶子节点，\(i\) 的左儿子编号为 \(2 \times i\)，右儿子编号为 \(2 \times i + 1\)。用程序写出来就是：

int ls(int x) {
  return x << 1;
}
int rs(int x) {
  return x << 1 | 1;
}

这时候就有小朋友会问了，为什么这里会用到左移和或呢？

左移操作就是在二进制最后在加上一个 \(0\)，那每一个 \(1\) 都往前了一位，所以每个 \(1\) 代表的十进制数，就变成了原来的 \(2\) 倍。

因为左移完了之后最后一位必定为 \(0\)，将 \(0\) 或上 \(1\)，得到 \(1\)，这样我们就把最末尾的 \(0\) 改成了 \(1\)，所以就加上了 \(1\)。

所以 \(x << 1 = 2 \times x,x << 1 | 1 = 2 \times x + 1\)。

因为二叉树的节点个数接近于 \(4n\)，所以线段树

要开四倍空间！

要开四倍空间！！

要开四倍空间！！！

某位曹姓巨佬就因为没开四倍空间而挂掉。

为了方便，在下文的讲解和代码中，会采用以下名称：

  • \(t\) 数组，即线段树数组；
  • \(a\) 数组，即初始数组；
  • \(tag\) 数组，即存储 \(\text{tag}\) 的数组；
  • \(n\)，即初始数组的大小；
  • \(x\)，当前遍历到的节点编号；
  • \(l\)，当前遍历到的区间左端点；
  • \(r\)，当前遍历到的区间右端点；
  • \(mid\)，当前遍历到的区间中点；
  • \(ul\)，要修改的区间左端点；
  • \(ur\)，要修改的区间右端点；
  • \(x\)，要修改区间要加上的值；
  • \(ql\)，要查找的区间左端点；
  • \(qr\)，要查找的区间右端点。

接下来，我们就一个一个的来看线段树里面的函数吧！

\(\text{PushUp}\)

不多说，最简单也是最短的一个函数。

因为非叶子节点的和就是它的两个子节点的和，所以我们要把子节点的和上传到父亲节点。

代码：

void PushUp(int x) {
  t[x] = t[ls(x)] + r[rs(x)];
}

\(\text{Build}\)

从名字可以看出，就是建树，但是在建的过程中，还要将 \(\text{tag}\) 初始化一下。至于 \(\text{tag}\) 是什么，等我们讲到 \(\text{AddTag}\) 的时候再说。

我们来看建树的具体步骤：

  1. 初始化 \(\text{tag}\) 为 \(0\)；
  2. 如果当前节点只有一个数，那么直接更新；
  3. 继续遍历左右儿子；
  4. \(\text{PushDown}\) 更新 \(t_x\)。

代码：

void Build(LL x, LL l, LL r) {
  tag[x] = 0;
  if (l == r) {
    t[x] = a[l];
    return;
  }
  LL mid = (l + r) >> 1;
  Build(ls(x), l, mid), Build(rs(x), mid + 1, r);
  PushUp(x);
}

\(\text{ex_Update}\)

看到标题，就有小朋友会问了：“啊你这普通 \(\text{Update}\) 还没讲就来讲加强版干什么啊？”

我只想说，这里的 \(\text{ex}\) 不是指的加强，而是：恶心！

你想，你不用线段树暴力求解，你的 \(\text{Update}\) 的复杂度是 \(O(r-l+1)\) 也就是 \(O(n)\)。

但是你用这个 \(\text{ex_Update}\) 来修改的话，复杂度是 \(O(n \log n)\)，还不如暴力。

接下来，我们就来学习一下这个没用的 \(\text{ex_Update}\)

遍历到 \(x\) 这个区间时，有 \(2\) 种情况。

  1. 要修改的区间完全不在当前区间里，即 l > ur || r < ul，如果是这样直接跳过。
  2. 否则将这个区间加上它与要修改的区间重合部分乘要修改的值。

代码：

因为这个东西过于 \(\text{ex}\)，所以它被 \(\texttt{BLuemoon_}\) 删掉了。

\(\text{AddTag}\)

\(\text{tag}\) 就是解决 \(\text{ex_Update}\) 方法。

\(\text{tag}\)，全名 \(\text{lazy-tag}\)，懒标记。

\(\text{tag}\) 如其名，这就是为懒人准备的。

有多懒呢，你要更新一个区间，按道理你应该把这个节点的所有子节点，子节点的子节点，子节点的子节点的子节点……，全部遍历一遍，这就是 \(\text{ex_Update}\) 为什么复杂度甚至高于暴力的原因。

我们给某个点打上懒标记，并标记上此时的 \(k\) 是多少，然后把这个区间加上它应该加的就行了。

注意：这里的 \(\text{tag}\) 应该使用 += 来更新，因为它可能原来还有没有下穿的懒标记

代码：

void AddTag(int x, int l, int r, int p) {
  tag[x] += p, t[x] += p * (r - l + 1);
}

\(\text{PushDown}\)

下传懒标记。

如果这个点被标记了，那么它的所有子孙节点都应该加上对应的数，而我们只改了 \(t_x\) 的值，所以我们要不懒标记下传。步骤如下：

  1. 如果这个点没有懒标记，直接返回。
  2. 把左右儿子全部打上一样的懒标记。
  3. 把自己的懒标记清零。

注意：我们的 \(\text{tag}\) 存储的是 \(k\)，而不是 \(k \times (r - l + 1)\)，所以下传的时候不需要将原懒标记除以二，直接下传原懒标记即可。

代码：

void PushDown(LL x, LL l, LL r) {
  if (tag[x]) {
    LL mid = (l + r) >> 1;
    AddTag(ls(x), l, mid, tag[x]), AddTag(rs(x), mid + 1, r, tag[x]);
    tag[x] = 0;
  }
}

\(\text{Update}\)

这次是正经的 \(\text{Update}\) 了。

步骤：

  1. 如果要修改区间完全包含当前区间，则直接 \(\text{AddTag}\)，并返回。
  2. 下传标记，这里不需要判断有没有标记，\(\text{PushDown}\) 里面有判断。
  3. 如果左儿子和要修改区间有并集，则递归修改左儿子。
  4. 如果右儿子和要修改区间有并集，则递归修改右儿子。
  5. \(\text{PushUp}\)。

代码：

void Update(LL ul, LL ur, LL x, LL l, LL r, LL k) {
  if (ul <= l && r <= ur) {
    AddTag(x, l, r, k);
    return;
  }
  PushDown(x, l, r);
  LL mid = (l + r) >> 1;
  if (ul <= mid) {
    Update(ul, ur, ls(x), l, mid, k);
  }
  if (mid < ur) {
    Update(ul, ur, rs(x), mid + 1, r, k);
  }
  PushUp(x);
}

\(\text{Query}\)

加油！这已经是最后一个函数了。如果你看完这里，那么恭喜你，已经学会线段树了！

这也是唯一一个有返回值的函数，它返回的是 \(\sum_{i=l}^{r}a_i\)。不然呢？

步骤：

  1. 如果要查询区间完全包含当前区间，直接返回 \(t_x\)。
  2. 下传懒标记，一定不要忘了这一步，因为 \(\text{Update}\) 和 \(\text{Query}\) 是混着来的，在查询的时候也可能遇到没有下传的懒标记，如果不下传，那么就这递归就会让答案变小。
  3. 如果左儿子和要查询区间有并集，则递归查询左儿子，当前答案加上左儿子的和。
  4. 如果右儿子和要查询区间有并集，则递归查询右儿子，当前答案加上右儿子的和。
  5. 返回答案，这里不需要 \(\text{PushUp}\)。你自己都没有修改为什么要修改上面的

代码：

LL Query(LL ql, LL qr, LL x, LL l, LL r) {
  if (ql <= l && r <= qr) {
    return t[x];
  }
  PushDown(x, l, r);
  LL mid = (l + r) >> 1, ans = 0;
  if (ql <= mid) {
    ans += Query(ql, qr, ls(x), l, mid);
  }
  if (mid < qr) {
    ans += Query(ql, qr, rs(x), mid + 1, r);
  }
  return ans;
}

P3372完整代码

// J2023 | BLuemoon_
#include <bits/stdc++.h>

using namespace std;
using LL = long long;

const int kMaxN = 1e5 + 5;

LL ls(LL x) {
  return x << 1;
}
LL rs(LL x) {
  return x << 1 | 1;
}

struct SegmentTree {
  LL n, a[kMaxN << 2], t[kMaxN << 2], tag[kMaxN << 2];
  void PushUp(LL x) {
    t[x] = t[ls(x)] + t[rs(x)];
  }
  void Build(LL x, LL l, LL r) {
    tag[x] = 0;
    if (l == r) {
      t[x] = a[l];
      return;
    }
    LL mid = (l + r) >> 1;
    Build(ls(x), l, mid), Build(rs(x), mid + 1, r);
    PushUp(x);
  }
  void AddTag(int x, int l, int r, int p) {
    tag[x] += p, t[x] += p * (r - l + 1);
  }
  void PushDown(LL x, LL l, LL r) {
    if (tag[x]) {
      LL mid = (l + r) >> 1;
      AddTag(ls(x), l, mid, tag[x]), AddTag(rs(x), mid + 1, r, tag[x]);
      tag[x] = 0;
    }
  }
  void Update(LL ul, LL ur, LL x, LL l, LL r, LL k) {
    if (ul <= l && r <= ur) {
      AddTag(x, l, r, k);
      return;
    }
    PushDown(x, l, r);
    LL mid = (l + r) >> 1;
    if (ul <= mid) {
      Update(ul, ur, ls(x), l, mid, k);
    }
    if (mid < ur) {
      Update(ul, ur, rs(x), mid + 1, r, k);
    }
    PushUp(x);
  }
  LL Query(LL ql, LL qr, LL x, LL l, LL r) {
    if (ql <= l && r <= qr) {
      return t[x];
    }
    PushDown(x, l, r);
    LL mid = (l + r) >> 1, ans = 0;
    if (ql <= mid) {
      ans += Query(ql, qr, ls(x), l, mid);
    }
    if (mid < qr) {
      ans += Query(ql, qr, rs(x), mid + 1, r);
    }
    return ans;
  }
};

SegmentTree tr;
LL m, op, x, y, k;

int main() {
  cin >> tr.n >> m;
  for (LL i = 1; i <= tr.n; i++) {
    cin >> tr.a[i];
  }
  tr.Build(1, 1, tr.n);
  for (; m; m--) {
    cin >> op;
    if (op == 1) {
      cin >> x >> y >> k;
      tr.Update(x, y, 1, 1, tr.n, k);
    } else {
      cin >> x >> y;
      cout << tr.Query(x, y, 1, 1, tr.n) << '\n';
    }
  }
  return 0;
}

线段树板子封装结构体：

struct SegmentTree {
  LL n, a[kMaxN << 2], t[kMaxN << 2], tag[kMaxN << 2];
  void PushUp(LL x) {
    t[x] = t[ls(x)] + t[rs(x)];
  }
  void Build(LL x, LL l, LL r) {
    tag[x] = 0;
    if (l == r) {
      t[x] = a[l];
      return;
    }
    LL mid = (l + r) >> 1;
    Build(ls(x), l, mid), Build(rs(x), mid + 1, r);
    PushUp(x);
  }
  void AddTag(int x, int l, int r, int p) {
    tag[x] += p, t[x] += p * (r - l + 1);
  }
  void PushDown(LL x, LL l, LL r) {
    if (tag[x]) {
      LL mid = (l + r) >> 1;
      AddTag(ls(x), l, mid, tag[x]), AddTag(rs(x), mid + 1, r, tag[x]);
      tag[x] = 0;
    }
  }
  void Update(LL ul, LL ur, LL x, LL l, LL r, LL k) {
    if (ul <= l && r <= ur) {
      AddTag(x, l, r, k);
      return;
    }
    PushDown(x, l, r);
    LL mid = (l + r) >> 1;
    if (ul <= mid) {
      Update(ul, ur, ls(x), l, mid, k);
    }
    if (mid < ur) {
      Update(ul, ur, rs(x), mid + 1, r, k);
    }
    PushUp(x);
  }
  LL Query(LL ql, LL qr, LL x, LL l, LL r) {
    if (ql <= l && r <= qr) {
      return t[x];
    }
    PushDown(x, l, r);
    LL mid = (l + r) >> 1, ans = 0;
    if (ql <= mid) {
      ans += Query(ql, qr, ls(x), l, mid);
    }
    if (mid < qr) {
      ans += Query(ql, qr, rs(x), mid + 1, r);
    }
    return ans;
  }
};

这样，你就学会了普通线段树的全部内容了，当然还有主席树，动态开点线段树，线段树合并，线段树分裂，李超线段树等等等等等等等等等等等等等……

当然，这些变种作者也不会

但是——

至少，你可以 AC 一道黄题了；至少，你可以在树状数组 TLE 的时候从容的写出一个线段树了；至少，你学会了一个 CCF \(5\) 级考点了；至少，你可以像某曹姓巨佬一样，只要看到数列就想到线段树了。

恭喜你，学会了线段树！

这就是本文的全部内容了，请帮我点一个赞然后关注我吗\(QwQ\)。

这篇文章的 Markdown 有428行，总字符数可以在标题下面看到，文件一共 \(12.2\) KB，看在我码了这么多字的份上，你真的不点一个赞吗？

标签：text,线段,mid,笔记,tag,区间,LL
From： https://www.cnblogs.com/bluemoon-blog/p/17742514.html

相关文章

  • 线段树模板
    应该是做的最认真的模板了。。。namespacexds{template<classT,constintMYMAXSIZE,T(*fun)(Ta,Tb)>classSTree{private:Tt[MYMAXSIZE<<2],tag[MYMAXSIZE<<2],a[MYMAXSIZE];intnum;inlineconstintls(constintx){......
  • 【数据结构】- 线段树
    线段树简介线段树是可以维护区间信息的数据结构。线段树将每个长度不为\(1\)的区间划分成左右两个区间递归求解，故把整个线段划分为一个树形结构，通过合并左右两区间信息来求得该区间的信息。根据建树方式可分为普通线段树和动态开点线段树。根据区间信息可分为普通线段树......
  • Linux运维学习笔记
    此笔记为学习https://www.bilibili.com/video/BV1nW411L7xm/?vd_source=3f851e85e66ef33269a2eefee664cec2的学习记录，目前持续更新中，希望能找到运维的实习吖 Ｏ(≧▽≦)ＯLinux的终端终端组成部分Linux关机命令shoutdown-hnow（正常关机）halt(关闭内存)init0使用VMware备......
  • 活动报名与缴费小程序开发笔记一
    项目背景活动报名与缴费小程序的开发背景主要源于以下几个因素：1.数字化时代的需求：随着移动互联网和智能手机的普及，人们习惯使用手机进行各种活动。传统的纸质报名表格和线下缴费方式变得相对繁琐，而数字化报名与缴费小程序提供了更便捷的解决方案。2.提高效率和减少人力成本：对于活......
  • 流畅的python笔记 （二） 2.序列构成的数组
    内置序列类型分类1：容器序列(能存放不同类型)：list,tuple,collections.deque扁平序列(不能存放不同类型)：str,bytes,bytearray,memoryview,array.array分类2:可变序列(能被修改):list,bytearray,array.array,collections.deque,memoryview不可变序列:tuple,str,bytes列表推导......
  • Python笔记
    第一章、Python概述1.1 扩展库安装方法使用pip命令安装扩展库。在cmd命令行中输入pip，回车后可以看到pip命令的使用说明。1.2 常用的pip命令pip命令示例说明pipfreeze[>requirements.txt]列出已安装扩展库及其版本号（不知道怎么用。。？）pipinstallSomePacka......
  • note 线段树
    适用场景：不断区间修改、区间询问。假设我们要区间求和，\(tree\)的含义：区间的和，其两个子节点为这个区间分为两半的和。我们把一个数组\(a\)看作一颗树\(tree\)，例：112333对应的\(tree\)（\(()\)里是编号，\([]\)里是对应的区间）：(1)13[1,6]/......
  • 线段树专题复习
    今天的主题是线段树专题复习！（什么？是昨天的？不听不听，只要我不说都不知道我鸽了一天！）好了，言归正传，我们来看一下今天的知识点们吧。Part1线段树自己不想讲了，想看的移步其他博客想看踢我，今天没时间了Part2一些优化ZKW线段树俗称重口味线段树，是一种不用递归实现的线段树，常数和......
  • 【做题笔记】dp，但是国庆限定版
    Day1方块消除传送门看到这个数据范围就可以猜测正解是\(O(n^4)\)的dp，与这个差不多相符合的可以想到区间dp。然后大胆猜测一下就是区间dp，令\(dp[i][j]\)表示消除掉\([i,j]\)后的最大价值，这个显然可以从长度更短的区间转移过来。所以此题我们可以从区间dp的方向思考......
  • 《敏捷软件需求》阅读笔记一
    以下是关于敏捷软件需求这本书籍的前八章的阅读心得体会，涵盖了每章的主要观点和个人体会：第一章：敏捷方法概述    第一章介绍了敏捷方法的起源和核心原则，其中最关键的原则是个体与交互、工作的软件、客户合作和响应变化。我学到了敏捷方法的灵活性和迭代开发是应对不断变化......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99