这场彻底打崩了,只做了 A,B,C ,可以看出我离退役已经不远力!
A. Glory Addicts
trash 题不写。感觉出得很没意思。
B. Prefix Sum Addicts
用 \(s_{n-k+1}\sim s_n\) 可以算出 \(a_{n-k+2}\sim a_n\) 。
另一方面,对于 \(a_1\sim a_{n-k+1}\) ,它们都不大于 \(a_{n-k+2}\) ,并且和为 \(s_{n-k+1}\) 。
容易得出结论:满足题意的 \(a\) 存在,当且仅当 \(a_{n-k+2}\sim a_n\) 单调不降,并且 \((n-k+1)a_{n-k+2}\ge s_{n-k+1}\) 。
View Code
#include<stdio.h>
const int N=1e5+5;
int T,n,k,s[N];
bool check() {
if (k==1) return 1;
for (int i=2; i<k; ++i)
if (s[i]-s[i-1]>s[i+1]-s[i]) return 0;
return 1ll*(n-k+1)*(s[2]-s[1])>=s[1];
}
int main() {
scanf("%d",&T);
while (T--) {
scanf("%d%d",&n,&k);
for (int i=1; i<=k; ++i)
scanf("%d",s+i);
puts(check()?"YES":"NO");
}
return 0;
}
C. Even Number Addicts
这题更是歌姬吧。
显然胜负只与奇数的个数、偶数的个数有关。
手玩小数据,找规律即可。
赛时大幅降智,好几次找的都是假规律,罚时罚麻了。
正确的规律见代码。
View Code
#include<stdio.h>
int T,n,x,s;
int main() {
scanf("%d",&T);
while (T--) {
scanf("%d",&n),s=0;
for (int i=1; i<=n; ++i)
scanf("%d",&x),s+=(x&1); //s表示奇数个数
if (s%4==0||s%4==3) puts("Alice");
else if (s%4==2) puts("Bob");
else puts((n-s&1)?"Alice":"Bob");
}
return 0;
}
D. Permutation Addicts
阅读理解题。真的离谱。不会出题可以不出。
我们观察 \(b\) 的定义,容易发现:若 \(x\le k\),则 \(b_x>k\) ;反之亦然。
因此,若 \(x<b_x\) ,则 \(k\ge x\) ;若 \(x>b_x\) ,则 \(k<x\) 。
于是我们可以通过 \(b\) 得到 \(k\) 与 \(x=1,2,\cdots,n\) 的大小关系,这样就确定了 \(k\) 。
接下来是求 \(a\) 的部分。
这个比较抽象,举个例子好了。
例如 \(n=8,k=5,a=[1,2,3,6,7,8,4,5]\) 。
计算可得 \(b=[9,9,9,3,3,3,6,6]\) 。
如果我们对于每个 \(x\) ,从 \(x\) 到 \(b_x\) 连一条边,那么图会长成这样:
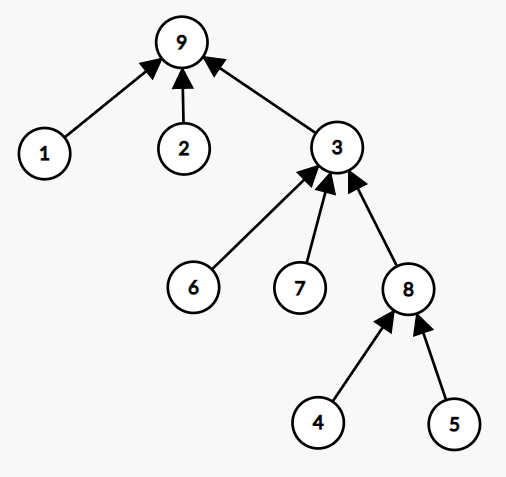
然后就容易想到怎么求 \(a\) 了:
-
先找到根节点。(根节点一定是 \(0\) 或 \(n+1\) ,取度数不为 0 的那个)
-
根节点的所有儿子中,一定只有一个不是叶子节点,它必须放在其它儿子之后。(其它儿子之间可以随便排列)
-
以这个儿子为新的根节点,重复第 2 步。
代码如下。
View Code
#include<stdio.h>
#include<vector>
const int N=1e5+5;
int T,n,m,k,l,r,b[N],d[N],Q[N];
std::vector<int>E[N];
inline int max(int x,int y) { return x>y?x:y; }
void solve() {
scanf("%d",&n),m=k=0;
for (int i=0; i<=n+1; ++i)
E[i].clear(),d[i]=0;
for (int i=1; i<=n; ++i) {
scanf("%d",b+i);
E[b[i]].push_back(i),++d[b[i]];
if (b[i]>i) k=max(k,i);
}
printf("%d\n",k);
l=r=0,Q[0]=(d[0]?0:n+1);
while (l<=r) {
if (l) printf("%d ",Q[l]);
int x=Q[l++];
for (int i=0; i<d[x]; ++i)
if (d[E[x][i]]) Q[++r]=E[x][i];
else printf("%d ",E[x][i]);
}
putchar('\n');
}
int main() {
scanf("%d",&T);
while (T--) solve();
return 0;
}
E. Balance Addicts
稍微思考之后可以发现,如果 \(a_i\) 均不为 0 ,那么这个题就会变得非常 sb 。
显然关键在于如何处理 0 。
首先,如果 \(a_1=a_2=\cdots=a_n=0\) ,那么随便划分即可,方案数为 \(2^n\) 。
否则,设 \(a\) 包含 \(x\) 个前缀 0 和 \(y\) 个后缀 0 。
先讨论 \(x,y\) 均不为 0 的情况,因为只有这种情况下,这些 0 会对总方案数产生影响。
考虑划分方案对应的 \(s\) ,显然 \(s\) 的两端各有 \(0\sim \min\{x,y\}\) 个 0 。
设 \(s\) 的两端各有 \(k\) 个 0 ,考虑在 \(a\) 中插板:
\[0~|~0~|~0~|~114~\cdots~514~|~0~|~0 \]两端都要插 \(k\) 个板,因此方案数为 \(\dbinom xk\dbinom yk\) 。
那么可以写出式子:
\[f(1,n)=\left(\sum_{k=0}^{\min\{x,y\}}\binom xk\binom yk\right)f(1+x,n-y) \]其中 \(f(l,r)\) 表示 \(a_l,\cdots,a_r\) 这个子段对应的答案。
然后是 \(xy=0\) 的情况,此时前缀 0 和后缀 0 不会影响划分方案数。
设 \(i,j\) 满足:\(a\) 中的前 \(i\) 个元素和后 \(j\) 个元素相等,并且 \(i,j\) 都最小。
双指针扫一下即可求出 \(i,j\) 。
如果 \(i=j=n\),那么显然 \(f(1,n)=1\) 。
否则,由 \(i,j\) 的最小性,我们可以得到:
-
\(a_1\sim a_i\) 与 \(a_{n-j+1}\sim a_n\) 一定没有公共元素,也就是说它们是不重叠的两段。
假设有重叠部分,将其消去,则会得到更小的 \(i,j\) 。 -
最终的划分方案中,这两段的内部都不能再断开。
假设能断开,则同样会出现更小的 \(i,j\) 。
既然不能断开,那么可以认为 \(a_1\sim a_i\) 等价于一个前缀 0 ,\(a_{n-j+1}\sim a_n\) 等价于一个后缀 0 。
然后用和前面类似的方法处理即可。
时间复杂度为 \(O(n)\) ,因为每个位置只被访问到一次。
#include<stdio.h>
typedef long long ll;
const int N=1e5+5,P=998244353;
int T,n,a[N],fac[N],inv[N]; ll S;
inline int power(int x,int y) {
int s=1;
while (y) {
if (y&1) s=1ll*s*x%P;
x=1ll*x*x%P,y>>=1;
}
return s;
}
inline int C(int n,int m) {
return 1ll*inv[n-m]*inv[m]%P*fac[n]%P;
}
int f(int l,int r) {
if (!S) return power(2,r-l);
int x=0,y=0;
while (!a[l]) ++l,++x;
while (!a[r]) --r,++y;
if (x&&y) {
int s=0;
for (int i=0; i<=x&&i<=y; ++i)
s=(1ll*C(x,i)*C(y,i)+s)%P;
return 1ll*s*f(l,r)%P;
}
ll sl=0,sr=0;
while (l<=r) {
sl+=a[l],S-=a[l],++l;
while (sr<sl) sr+=a[r],S-=a[r],--r;
if (sl==sr) break;
}
if ((--l)<(++r)&&sl==sr)
return a[l]=a[r]=0,f(l,r);
return 1;
}
int main() {
n=100000,fac[0]=1;
for (int i=1; i<=n; ++i)
fac[i]=1ll*fac[i-1]*i%P;
inv[n]=power(fac[n],P-2);
for (int i=n; i; --i)
inv[i-1]=1ll*inv[i]*i%P;
scanf("%d",&T);
while (T--) {
scanf("%d",&n),S=0;
for (int i=1; i<=n; ++i)
scanf("%d",a+i),S+=a[i];
printf("%d\n",f(1,n));
}
return 0;
}