【模板】轻重链剖分/树链剖分
题目描述
如题,已知一棵包含 \(N\) 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
-
1 x y z,表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。 -
2 x y,表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。 -
3 x z,表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。 -
4 x表示求以 \(x\) 为根节点的子树内所有节点值之和
输入格式
第一行包含 \(4\) 个正整数 \(N,M,R,P\),分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含 \(N\) 个非负整数,分别依次表示各个节点上初始的数值。
接下来 \(N-1\) 行每行包含两个整数 \(x,y\),表示点 \(x\) 和点 \(y\) 之间连有一条边(保证无环且连通)。
接下来 \(M\) 行每行包含若干个正整数,每行表示一个操作。
输出格式
输出包含若干行,分别依次表示每个操作 \(2\) 或操作 \(4\) 所得的结果(对 \(P\) 取模)。
样例 #1
样例输入 #1
5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
样例输出 #1
2
21
提示
【数据规模】
对于 \(30\%\) 的数据: \(1 \leq N \leq 10\),\(1 \leq M \leq 10\);
对于 \(70\%\) 的数据: \(1 \leq N \leq {10}^3\),\(1 \leq M \leq {10}^3\);
对于 \(100\%\) 的数据: \(1\le N \leq {10}^5\),\(1\le M \leq {10}^5\),\(1\le R\le N\),\(1\le P \le 2^{31}-1\)。
【样例说明】
树的结构如下:
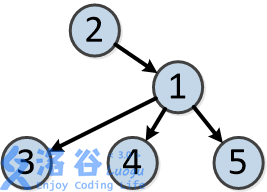
各个操作如下:
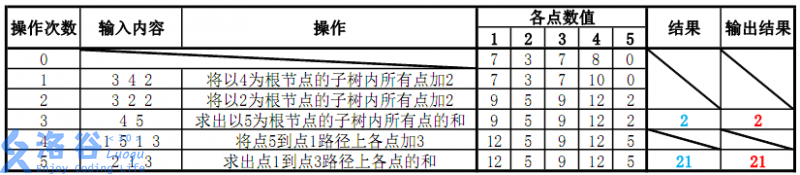
故输出应依次为 \(2\) 和 \(21\)。
解题思路
这是一道树剖的板子题,树剖部分的解释在代码里,线段树部分作为前置知识不再解释
ps:军理课闲的没事看了看kruskal重构树,课后去洛谷找了一道能用kruskal重构树的简单题P1967 [NOIP2013 提高组] 货车运输,在看题解学习怎么用重构树写这题的时候又遇到了两遍dfs求lca这个东西,而这个东西树剖里有,但一直不会,于是就把树剖学了)))以后lca只用树剖写!毕竟常数小)
代码
// Problem: P3384 【模板】轻重链剖分/树链剖分
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3384
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Time: 2022-10-01 16:48:48
//
// Powered by CP Editor (https://cpeditor.org)
//fw
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<set>
#include<map>
#include<unordered_map>
#include<stack>
#include<cmath>
#define IOS ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);
#define debug(a) cout<<#a<<"="<<a<<endl;
#define sv(a,l,r,x) for(int i=l;i<=r;i++)a[i]=x;
#define pii pair <int, int>
#define endl '\n'
#define pb push_back
#define lc u<<1
#define rc u<<1|1
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int N=1e5+10,M=2*N;
int n,m,r,p;
struct node
{
int l,r;
ll sum,add;
}tr[N<<2];
int h[N],e[M],ne[M],w[M],idx;
int id[N],nw[N],fa[N],dep[N],top[N],sz[N],son[N],cnt;
void add(int a,int b)
{
e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
void pushup(int u)
{
tr[u].sum=tr[lc].sum+tr[rc].sum;
}
void pushdown(int u)
{
auto &root=tr[u],&l=tr[lc],&r=tr[rc];
if(root.add)
{
l.add+=root.add;
r.add+=root.add;
l.sum+=(l.r-l.l+1)*root.add;
r.sum+=(r.r-r.l+1)*root.add;
root.add=0;
}
}
void build(int u,int l,int r)
{
if(l==r)
{
tr[u]={l,r,nw[l],0};
return;
}
tr[u]={l,r};
int mid=l+r>>1;
build(lc,l,mid);
build(rc,mid+1,r);
pushup(u);
}
ll query(int u,int l,int r)
{
if(tr[u].l>=l&&tr[u].r<=r)
{
return tr[u].sum;
}
ll ans=0;
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
if(l<=mid)ans+=query(lc,l,r);
if(r>mid)ans+=query(rc,l,r);
return ans;
}
void modify(int u,int l,int r,int k)
{
if(tr[u].l>=l&&tr[u].r<=r)
{
tr[u].sum+=(tr[u].r-tr[u].l+1)*k;
tr[u].add+=k;
return ;
}
int mid=tr[u].l+tr[u].r>>1;
pushdown(u);
if(l<=mid)modify(lc,l,r,k);
if(r>mid)modify(rc,l,r,k);
pushup(u);
}
void dfs1(int u,int father,int depth)//当前节点,父节点,当前深度
{
fa[u]=father;dep[u]=depth;sz[u]=1;
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(j==father)continue;
dfs1(j,u,depth+1);
sz[u]+=sz[j];//累加子树大小
if(sz[son[u]]<sz[j])son[u]=j;//更新重儿子
}
}
void dfs2(int u,int t)//当前点,当前重链的顶点
{
id[u]=++cnt;nw[cnt]=w[u];//给点赋予dfs序,并把这个点的值转移到dfs序对应点上
top[u]=t;//存储这个点所在重链的顶点
if(!son[u])return;//如果是叶子节点则没有重儿子,直接返回
//优先遍历重链上的点,使得重链上点的dfs序连续
//因为修改查询的时候是一段一段的修改 当前点->重链顶点 再跳过去,优先搜索重儿子可以使修改查询的每一段连续,便于线段树维护区间
dfs2(son[u],t);
//搜索重儿子以外的点
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(j==fa[u]||j==son[u])continue;
dfs2(j,j);//对于重儿子以外的点,这条重链的顶点就是这个非重儿子自己
}
}
ll query_tree(int u)//因为子树的dfs序是“连续“的,根节点的dfs最先遍历到的点,最后一个点的dfs序显然是根节点的dfs序+子树大小-1
{
return query(1,id[u],id[u]+sz[u]-1);
}
//子树修改和查询同理,改个函数名就行
void modify_tree(int u,int k)
{
modify(1,id[u],id[u]+sz[u]-1,k);
}
//路径的操作是终点,基本思路和倍增lca有点类似,
void modify_path(int u,int v,int k)
{
while(top[u]!=top[v])//若两个点的重链顶点不同,则说明不在一条重链上
{
if(dep[top[u]]<dep[top[v]])swap(u,v);//把u换成重链顶点深度较深的点,然后开始先上跳
modify(1,id[top[u]],id[u],k);//修改当前点-重链顶点这一段,因为线段树是建立在dfs序上,所以需要套一个id数组
//因为顶点的深度浅,所以先被遍历到,dfs序也就小,所以是修改id[top[u]]-id[u]这一段
//因为操作都是闭区间,顶点已经被操作过了,所以需要跳到他的父节点
u=fa[top[u]];//跳到顶点的父节点,准备修改下一段
}
//此时两个点已经在一条链上了,只需要修改最后一段即可
if(dep[u]<dep[v])swap(u,v);//使u换成深度大的点
modify(1,id[v],id[u],k);//修改最后一段
}
//和路径修改基本一致,只是改个函数名加个计算res
ll query_path(int u,int v)
{
ll res=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]])swap(u,v);
res+=query(1,id[top[u]],id[u]);
u=fa[top[u]];
}
if(dep[u]<dep[v])swap(u,v);
res+=query(1,id[v],id[u]);
return res;
}
int main()
{
memset(h,-1,sizeof h);//前向星初始化
cin>>n>>m>>r>>p;
for(int i=1;i<=n;i++)cin>>w[i];//每个点的初始值
for(int i=1;i<=n-1;i++)
{
int a,b;
cin>>a>>b;
add(a,b);add(b,a);//加边
}
//两遍dfs预处理出所需信息
dfs1(r,0,1); //预处理出父节点、深度、子树大小、重儿子
dfs2(r,r);
//在树dfs序上建线段树
build(1,1,n);
//处理查询
while(m--)
{
int t,u,v,k;
cin>>t>>u;
if(t==1)
{
cin>>v>>k;
modify_path(u,v,k);
}
else if (t==3)
{
cin>>k;
modify_tree(u,k);
}
else if (t==2)
{
cin>>v;
printf("%lld\n",query_path(u,v)%p);
}
else printf("%lld\n",query_tree(u)%p);
}
return 0;
}