在动态博弈中,行动有先后次序;在不完全信息条件下,博弈的每一参与人知道其他参与人的有哪几种类型以及各种类型出现的概率,即知道“自然”参与人的不同类型与相应选择之间的关系,但是,参与人并不知道其他的参与人具体属于哪一种类型。由于行动有先后顺序,后行动者可以通过观察先行动者的行为,获得有关先行动者的信息,从而证实或修正自己对先行动者的行动。在不完全信息动态博弈一开始,某一参与人根据其他参与人的不同类型及其所属类型的概率分布,建立自己的初步判断。当博弈开始后,该参与人就可以根据他所观察到的其他参与人的实际行动,来修正自己的初步判断。并根据这种不断变化的判断,选择自己的策略。

一、不完全信息动态博弈案例
1.1黔驴技穷
精炼贝叶斯均衡是完全信息动态博弈的子博弈精炼纳什均衡与不完全信息静态博弈的贝叶斯纳什均衡的结合。贝叶斯方法是概率统计中的一种分析方法。它是指根据所观察到现象的有关特征,并对有关特征的概率分布的主观判断(即先验概率)进行修正的标准方法。中国著名成语故事黔驴技穷,就是贝叶斯方法思想的一个典型表达。
老虎没有见过驴子,因而不知道自己比驴子强还是弱。老虎的战略是:如果自己弱,那就只能躲,如果自己强,那就吃驴子。对于自己并不了解驴子,老虎的做法是不断试探,通过试探,修改自己对驴子的看法。如果驴子表现温顺无能,老虎就认为驴子是美食的概率比较大,起初驴子没有反应,老虎认为驴子不像强敌,胆子越来越大。后来驴子大叫,老虎以为驴子要吃它,吓的逃走,但后来想想,又觉得不一定,于是继续试探,直到驴子踢老虎,老虎才觉得驴子“仅此技耳”,于是采取自己强时的最优行动——吃驴子。
1.2 信号传递
由于信息不完全,每个人都希望向对方传递对自己有利的信号。比如,在招聘时,应聘者总是显示自己最好的一面。谈判中,企业总是把最能显示自己实力的一面展示出来。公司越来越注意企业形象的塑造。女孩子总是把自己打扮得漂亮。人们总是把最好的衣服穿在外面。等等。问题是,对方不一定相信你所传递的信号是真实的。有的信号,一下子是难以识别真伪的,需要时间。所以,“百年老店”是最好的信号传递方式。
为什么招聘单位看重学历,因为学历容易甄别,而且比起能力的描述来,相对可靠;为什么顾客喜欢买名牌产品,因为名牌是经过很多年才形成的,广告、产品质量、服务质量等因素起了很大的作用,名牌传递的信号就是:质量好,服务好。教育信号传递模型是分析劳动力市场上工人的教育水平如何传递有关能力的信息的模型。在这个模型里,企业的生产率取决于工人的能力。工人的能力可能高可能低,工人本人知道,雇主不知道;教育本身不改进工人的能力,但却可以传递有关这种能力的信息,原因是,教育要花费成本,而高能力的人的教育成本相对于低能力的人的要低,因为一个笨蛋要比一个聪明人遭受更大的痛苦才能完成必修的课程,拿到文凭。这样,文凭就成为能力的象征,尽管它不一定是能力的源泉。高能力的人要把自己与低能力的人分开,就要选择受更多的教育,企业看到受过教育的人就推断是高能力,支付高工资。如果这个模型是正确的话,我们也许不应该简单地因为所学内容无用就否定一种教育制度,如中国古代社会的科举制度,它或许也具有信号传递的功能。
1.3 企业招聘
假设工人按能力标准分析在[0,1] 区间。一般来说、高学历工人的劳动生产率高,低学历工人的劳动生产率也低。因此,假设工人素质与劳动生产率的关系可以用下图表示。图中横轴反映工人学历,从左至右对应于一个学历从高到低的工人。设图中 PP′代表各种学历工人对应的劳动生产率,劳动生产率与工人学历之间呈线性函数关系。
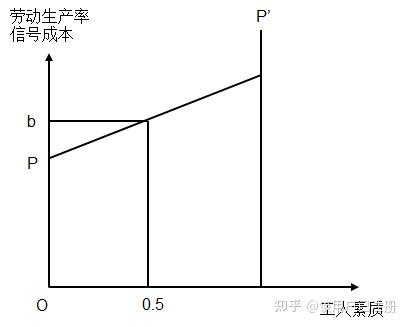
工人的学历和相应的劳动生产率如上图所示。如果企业不运用任何信号机制,随机选择工人,那么所招工人的平均期望学历是0.5,平均期望劳动生产率为 b,都属于平均水平。企业通常会运用信号机制,如对应聘者提学历要求或进行招工考试。设工人满足学历要求和通过考试的成本与工人的素质负相关,即成本是素质的线性减函数,如下图中的曲线 cc′所示。
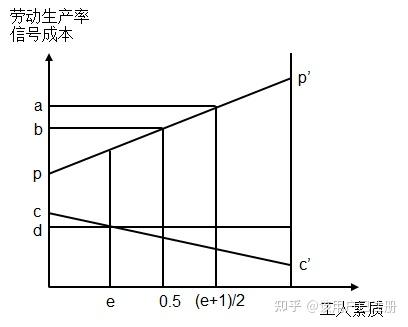
假设到该企业工作的收益是d,那么发出信号的成本低于d的工人,也就是素质高于e的人给企业发信号是合算的,有发信号的愿望,而素质低于e的人发信号的成本高于发信号的收益,因此没有发信号的意义。于是,企业最后录取的都是发出信号的高素质工人,这样企业通过采取上述学历要求作为筛选机制,就将素质低的人自然而然地排除掉,录用的工人的平均期望素质能够达到\(\frac{e+1}{2}\),工人的平均期望劳动生产率为\(a(a>b)\)。
二、精炼贝叶斯纳什均衡
在不完全信息动态博弈(dynamic game of incomplete information) 中,“自然”首先选择参与人的类型,参与人自己知道,其他参与人不知道;在自然选择之后,参与人开始行动,参与人的行动有先有后,后行动者能观测到先行动者的行动,但不能观测到先行动者的类型,因为参与人的行动是类型依存的,每个参与人的行动都传递着有关自己类型的某种信息,后行动者可以通过观察先行动者所选择的行为来推断其类型或修正对其类型的先验信息(概率分布),然后选择自己的最优行动。先行动者预测到自己的行动将被后行动者所利用,就会设法选择传递对自己最有利的信息,避免传递对自己不利的信息。因此,博弈过程不仅是参与人选择行动的过程,而且是参与人不断修正信念的过程。精炼贝叶斯均衡是不完全信息动态博弈均衡的基本均衡概念,它是泽尔腾(Selten)的完全信息动态博弈子博弈精炼纳什均衡和海萨尼(Harsanyi)的不完全信息静态博弈贝叶斯均衡的结合。精炼贝叶斯均衡要求,给定有关其他参与人的类型的信念,参与人的战略在每一个信息集开始的“后续博弈”上构成贝叶斯均衡;并且,在所有可能的情况下,参与人使用贝叶斯法则修正有关其他参与人的类型的信念。
让我们再一次考虑市场进入的例子。假定有两个时期\(t=1,2\),在\(t=1\), 市场上有一个垄断企业(“在位者”)在生产。一个潜在的进入者考虑是否进入;如果进入者进入,在\(t=2\),两个企业进行库诺特博弈,否则,在位者仍然是一个垄断者。假定在位者有两个可能的类型:高成本或低成本,进入者在博弈开始时只知道在位者是高成本的概率是\(\mu\),低成本的概率是 \(1-\mu\)。这个概率称为进入者的先验信念(prior beliefs)。假定进入者只有一个类型:进入成本为2;如果进入的话,生产成本函数与高成本的在位者成本函数相同。在 \(t=1\),在进入者决定是否进入之前,作为垄断者的在位者要决定该时期的价格(或生产量),假定只有三种可能的价格选择:\(p=4,\quad p=5或 p=6\)。如果在位者是高成本,对应三种价格选择的利润分别是:2、6或7;如果在位者是低成本,对应的利润分别是:6,9或8。因此。高成本在位者的单阶段最优垄断价格是\(p=6\),低成本的单阶段最优垄断价格是\(p=5\)(记住,最优垄断价格总是边际成本的增函数)。在\(t=2\) , 如果进入者已经进入,在位者的成本函数变成共同知识;如果在位者是高成本,两个企业的成本函数相同,对称的库诺特均衡产量下的价格为\(p=5\), 每个企业的利润是3,扣除进入成本2,进入者的净利润是1;如果在位者是低成本,两个企业的成本函数不同,非对称库诺特均衡产量下的价格是4,在位者的利润是5,进入者的利润是1,扣除进入成本2,进入者的净利润是-1。如果进入者不进入,\(t=2\)时期在位者仍然是一个垄断者,不同价格选择下的利润水平与第一阶段相同。我们构造了这些数字使得在完全信息情况下,如果在位者是高成本,进入者选择进入,如果在位者是低成本,进入者选择不进入。
下图是这个博弈的一个简化的扩展式表述。图中在位者有两个单结信息集,表示在位者知道“自然”的选择(自己的类型);三条虚线表示进入者有三个信息集,每个信息集有两个决策结(用虚线连接),表示进入者能观测到在位者的价格选择但不能观测到在位者的成本函数(即进入者观测到\(p=4,\quad p=5或 p=6\),但每一种价格可能是高成本在位者的选择也可能是低成本在位者的选择)。我们将第一阶段不同价格选择下的利润向量写在博弈树的终点结,尽管实际支付在进入者决定是否进入之前就已实现。注意,进入者第一阶段的利润恒为0。我们省略了第二阶段博弈的扩展式,代之以库诺特均衡支付向量和垄断利润。这样做的理由是,在博弈进入第二阶段后,如果进入者已经进入,库诺特均衡产量(和对应的价格)是每个企业的最优选择;如果进入者没有进入,单阶段垄断产量(和价格)是在位者的最优选择。

尽管当博弈进入第二阶段后,企业的行动选择是一个简单的静态博弈决策问题,但第一阶段的选择要复杂得多。进入者是否进入依赖于它对在位者成本函数的判断:给定在位者是高成本时进入的净利润是1,低成本时进入的净利润是 −1,当只当进入者认为在位者是高成本的概率大于1/2 时,进入者才会选择进入。这一点与我们在上一章讨论的不完全信息静态博弈的进入决策没有什么不同。但与静态博弈不同的是,现在,在观测到在位者第一阶段的价格选择后,进入者可以修正对在位者成本函数的先验概率\(\mu\),因为在位者的价格选择可能包含着有关其成本函数的信息。比如说,无论在何种情况下,低成本的在位者不会选择\(p=6\)(因为低成本的在位者不希望进入者认为自己是高成本),因此,如果进入者观测到在位者选择了\(p=6\),它就可以推断在位者一定是高成本,选择进入是有利可图的。预测到选择\(p=6\) 会招致进入者进入,即使高成本的在位者也有可能不会选择\(p=6\),尽管 \(p=6\)是单阶段的最优垄断价格。类似地,低成本的在位者也可能不会选择 \(p=5\),如果\(p=5\)会招致进入者进入的话。这里,问题的核心是在位者必须考虑价格选择的信息效应:不同的价格如何影响进入者的后验概率从而影响进入者的决策。一个非单阶段最优价格会减少现期利润,但如果它能阻止进入者进入,从而使在位者在第二阶段得到垄断利润而不是库诺特均衡利润,如果垄断利润与库诺特均衡利润之间的差距足够大,如果在位者有足够的耐心,选择一个非单阶段最优价格可能是最优的。我们将看到,在均衡情况下,在位者究竟选择什么价格。不仅与其成本函数有关,而且与进入者的先验概率\(\mu\)有关;而不论\(\mu\)为多少,单阶段最优垄断价格不构成一个均衡。
为了分析上述动态博弈的均衡结果,仅仅使用上一章定义的贝叶斯纳什均衡是不够的。这是因为,在静态贝叶斯均衡中,参与人的信念是事前给定的,均衡概念没有规定参与人如何修正自己的信念。但是,如果进入者可以任意地修正自己有关在位者成本函数地信念,上述不完全信息动态博弈可以有任意地贝叶斯均衡。比如说,假定\(\mu=\mu^*<1/2\) , 下列战略组合是一个贝叶斯均衡:不论在位者选择什么价格,进入者总是认为在位者是高成本的概率为\(\mu^*<1/2\) ,总是选择不进入;高成本的在位者选择 \(p=6\), 低成本的在位者选择\(p=5\)。这个战略组合是一个贝叶斯均衡,因为,给定信念\(\mu^*<1/2\) 和在位者的战略,进入者选择不进入是最优的;给定进入者总是选择不进入,在位者选择单阶段最优垄断价格是最优的(第一阶段的选择对第二阶段的结果没有影响)。很显然,这个均衡是不合理的,因为它包含一个不可置信的威胁;进入者不会修正对在位者成本函数的信念。给定\(p=6\)不可能是低成本在位者的最优选择,如果在位者选择了\(p=6\), 进入者为什么仍然认为在位者是最高成本的概率小于1/2 呢?
我们引入子博弈精炼纳什均衡概念剔除了那些包含不可置信威胁战略的纳什均衡。但在如上图所示的不完全信息动态博弈中,子博弈精炼纳什均衡并不能给我们直接帮助,因为不完全信息博弈只有一个子博弈,即从初始结开始的整个博弈,因此,所有的均衡都是子博弈精炼均衡。在上图中,进入者的每一个信息集都包含两个决策结,除非进入者知道自己处在每一个决策结上的概率,否则,他不可能做出决策。不过,尽管子博弈精炼均衡不能直接应用于上述博弈,但子博弈精炼均衡概念的逻辑是适用的。精炼纳什均衡要求均衡战略不仅在整个博弈上构成纳什均衡,而且要求在每个子博弈上构成纳什均衡。仿照这一逻辑,如果我们将从每一个信息集开始的博弈的剩余部分称为一个“后续博弈”(continuation game)(不同于子博弈,因为子博弈必须开始于单结信息集,并且不能切割信息集),一个“合理”的均衡应满足如下要求:给定每一个参与人有关其他参与人类型的后验信念,参与人的战略组合在每一个后续博弈上构成贝叶斯均衡。
但要求战略组合在每一个后续博弈上构成贝叶斯均衡仍然没有剔除“总是认为在位者是高成本的概率\(\mu^*<1/2\)" 这样不合理行为。剔除这种不合理行为的方式是,假定参与人(在所有可能的情况下)根据贝叶斯规则(Bayes' rule)修正先验信念;并且,每个参与人都假定其他参与人选择的是均衡战略。
精炼贝叶斯均衡(perfect Bayesian equilibrium)是贝叶斯均衡、子博弈精炼均衡和贝叶斯推断的结合。它要求:(1)在每一个信息集上,决策者必须有一个定义在属于该信息集的所有决策结上的一个概率分布(信念);(2)给定该信息集上的概率分布和其他参与人的后续战略,参与人的行动必须是最优的;(3)每一个参与人根据贝叶斯法则和均衡战略修正后验概率。
后续策略(subsequent strategy):是从给定信息集开始的后续博弈上的完备的行动规则。
2.1 贝叶斯法则
理解贝叶斯法则对理解精炼贝叶斯均衡概念是至关重要的。在给出精炼贝叶斯均衡的正式定义之前,我们先来解释一下贝叶斯法则。
在日常生活中,当面临不确定性时,在任何一个时点上,我们对某件事情发生的可能性有一个判断。然后,我们会根据新的信息来修正这个判断。统计学上,修正之前的判断称为“先验概率”(prior probability),修正之后的判断称为“后验概率”(posterior probability)。贝叶斯法则正是人们根据新的信息从先验概率得到后验概率的基本方法。
让我们以不完全信息博弈为例说明贝叶斯法则。如通常一样,我们假定参与人的类型是独立分布的。假定参与人\(i\)有\(K\)个可能的类型,有\(H\)个可能的行动。我们用\(\theta^k\) 和\(a^h\) 分别代表一个特定的类型和一个特定的行动(因为我们现在只考虑一个参与人,所以省略了下标\(i\))。假定 \(i\)属于类型\(\theta^k\)的先验概率是
给定 \(i\)属于 \(\theta^k\), \(i\)选择\(a^h\)的条件概率为
\[p(a^h|\theta^k),\quad \sum_hp(a^h|\theta^k)=1 \]那么\(i\)选择\(a^h\)的边缘概率是:
\[Prob\{a^h\}=p(a^h|\theta^1)p(\theta^1)+\cdots+p(a^h|\theta^K)p(\theta^K)=\sum\limits_{k=1}^Kp(a^h|\theta^k)p(\theta^k) \]即参与人\(i\)选择行动\(a^h\)的“总”概率是每一种类型的\(i\)选择\(a^h\)的条件概率 \(p(a^h|\theta^k)\)的加权平均,权数是他属于每种类型的先验概率\(p(\theta^k)\)。
2.2 精炼贝叶斯均衡
现在来给出精炼贝叶斯均衡概念的正式定义。假定有 \(n\) 个参与人,参与人 \(i\) 的类型是 \(\theta_i \in \Theta_i\) , \(\theta_i\) 是私人信息, \(p_i\left(\theta_{-i} \mid \theta_i\right)\) 是属于类型 \(\theta_i\) 的参与人 \(i\) 认为其他 \(n-1\) 个参与人属于类型 \(\theta_{-i}=\left(\theta_1, \cdots, \theta_{i-1}, \theta_{i+1}, \cdots, \theta_n\right)\) 的先验概率。令 \(S_i\) 是 \(i\) 的策略空间, \(s_i \in S_i\) 是一个特定的策略 (依赖于类型 \(\left.\theta_i\right), a_{-i}^h=\left(a_1^h, \cdots, a_{i-1}^h, a_{i+1}^h, \cdots, a_n^h\right)\) 是在第 \(h\) 个信息集上参与人 \(i\) 观测到的其他 \(n-1\) 个参与人的行动组和,它是策略组合
\(s_{-i}=\left(s_1, \cdots, s_{i-1}, s_{i+1}, \cdots, s_n\right)\) 的一部分(即 \(s_{-i}\) 规定的行动), \(\widetilde{P}_i\left(\theta_{-i} \mid a_{-i}^h\right)\) 是在观测到 \(a_{-i}^h\) 的情况下参与人 \(i\) 认为其他 \(n-1\) 个参与人属于类型
\(\theta_{-i}=\left(\theta_1, \cdots, \theta_{i-1}, \theta_{i+}, \cdots, \theta_n\right)\) 的后验概率, \(\tilde{p}_i\) 是所有后验概率 \(\tilde{p}_i\left(\theta_{-i} \mid a_{-i}^h\right)\) 的集合 (即 \(\tilde{p}_i\) 包括了参与人 \(i\) 在每一个信息集 \(h\) 上的后验概率), \(u_i\left(s_i, s_{-i}, \theta_i\right)\) 是 \(i\) 的效用函数。 那么,精炼贝叶斯均衡可以定义如下:
精炼贝叶斯均衡是一个策略组合 \(s^*(\theta)=\left(s_1^*\left(\theta_1\right), \cdots, s_n^*\left(\theta_n\right)\right)\) 和一个后验概率组合 \(\tilde{p}=\left(\tilde{p}_1, \cdots, \tilde{p}_n\right)\) ,满足:
\[s_i^*\left(s_{-i}, \theta_i\right) \in \arg \max _{s_i} \sum_{\theta_{-i}} \tilde{p}_i\left(\theta_{-i} \mid a_{-i}^h\right) u_i\left(s_i, s_{-i}, \theta_i\right) \text { ; } \]
(P) 对于所有的参与人 \(i\) ,在每一个信息集 \(h\) ,(B) \(\tilde{p}_i\left(\theta_{-i} \mid a_{-i}^h\right)\) 是使用贝叶斯法则从先验概率 \(p_i\left(\theta_{-i} \mid a_{-i}^h\right)\) ,观测到的 \(a_{-i}^h\) 和最优策略 \(s_{-i}^*(\cdot)\) 得到(在可能的情况下)。
三、信号传递
孔雀寓意着聪明、善良、自由、和平,一般孔雀象征着吉祥、幸福、高洁华贵,同时也表示长寿之意。孔雀是百鸟之王,是吉祥鸟,因此,孔雀受到了广大人民的喜爱与青睐,其观赏价值也是比较的高。孔雀是一种吉祥鸟,它体态优美,丹口玄目,细劲隆胸。而且也是最善良、最聪明、最爱自由与和平的鸟,是吉祥幸福的象征,孔雀也可以看为是绶带鸟绶与寿谐音,表示长寿之意。在希腊神话中,孔雀更是象征着赫拉女神。它能够给人带来好运,不断激励着人去前进。
信号博弈”是研究具有信息传递特征的信号机制的一般非完全信息动态博弈模型。信号博弈的基本特征是两个(或两类,每类又有若干个)博弈方,分别称为信号发出方(Sender)和信号接收方(Receiver),他们先后各选择一次行为,其中信号接收方具有不完全信息,但他们可以从信号发出方的行为中获得部分信息,信号发出方的行为对信号接收方来说,好像是一种(以某种方式)反映其有关得益信息的信号。这也正是这类博弈被称为“信号博弈”的原因。
由于信号博弈也是动态贝叶斯博弈,因此也可以通过海萨尼转换直接表示成完全但不完美信息动态博弈。设自然(博弈方0)先按特定的概率分布从信号发出方的类型空间中为发出方随机选择一个类型,并将该类型告诉发出方(即发出一个信号);然后是接收方在自己的行为空间中选择一个行为(也称发出一个信号);最后接收方根据发出方的行为选择自己的行为。如果我们用\(S\)表示信号发出方,用\(R\)表示信号接收方,用 \(T=\{t_{1},...,t_{I}\}\)表示\(S\)的类型空间,用\(M=\{m_{1},...,m_{J}\}\) 表示\(S\)的行为空间,或者称信号空间,用\(a=\{a_{1},...,a_{K}\}\)表示 \(R\)的行为空间,用\(u_{s}\)和\(u_{R}\)分别表示\(S\)和\(R\)的得益,并且自然为\(S\)选择类型的概率分布为$${p(t_{1}),...,p(t_{i})}$$。因此,信号博奔的时间顺序可表示为:
(1)博弈方0(自然)以概率\(p(t_{i})\)从可行的类型集\(T\)中为发送者 \(S\)选择类型\(t_{i}\),并让\(S\)知道,这里对所有的\(i\),\(p(t_{i})>0\) ,且 \(p(t_{1}),...,p(t_{I})=1\)。
(2)发送者\(S\)观测到\(t_{i}\)后,从可行的信号集\(M\)中选择行为 \(m_{j}\) 。
(3)接收者\(R\)看到\(m_{j}\),(但不能观测到\(t_{i}\))后从可行的行为空间中选择行为\(a_{k}\)。
(4)发送者\(S\)和接收者\(R\)的得益\(u_{s}\)和\(u_{R}\)都取决于\(t_{i}\) 、\(m_{j}\)和\(a_{k}\)。
注意 \(T\)、\(M\)和\(A\)既可以是离散空间,也可以是连续空间。
3.1 信号博弈精练贝叶斯均衡
这里,我们简单地将类型空间、可行信号集与可行行动集定义为有限集合,在实际应用中,它们常常表现为连续的区间,显然,此时可行信号集依赖于类型空间,而可行行动集则依赖于发送者发出的信号。这是一个简单的信号博弈,其中\(N\)表示自然,\(T=\{t_{1},t_{2}\}\), \(M=\{m_{1},m_{2}\}\),\(A=\{a_{1},a_{2}\}\) ,图中\(p\) 及\(1−p\)表示自然选择类型时的概率分布。
在信号博弈中,发送者的纯策略是根据自然抽取的可能类型来选取相应的信号,因此,信号可视作类型\(t\)的函数\(m(t_{i})\)。接收者的纯策略是信号的函数\(a(m_{j})\),即根据观察到的发送者发出的信号确定自已的行动。在下图的信号博弈中,发送者 \(S\)与接收者\(R\)各有四个纯策略。
发送者的纯策略:
发送者\(S\)的策略1,记为\(S(1)\):若自然抽取\(t_{1}\),选择 \(m_{1}\) ;若自然抽取\(t_{2}\),则选择\(m_{1}\);
发送者\(S\)的策略2,记为\(S(2)\):若自然抽取\(t_{1}\),选择 \(m_{1}\);若自然抽取\(t_{2}\),则选择 \(m_{2}\);
发送者\(S\)的策略3,记为\(S(3)\):若自然抽取\(t_{1}\),选择 \(m_{2}\);若自然抽取\(t_{2}\),则选择 \(m_{1}\);
发送者\(S\)的策略4,记为\(S(4)\):若自然抽取\(t_{1}\),选择 \(m_{2}\);若自然抽取\(t_{2}\),则选择 \(m_{2}\);
接收者的纯策略:
接收者\(R\)的策略1,记为\(R(1)\):若\(S\)发出\(m_{1}\),选择 \(a_{1}\);若 \(S\)发出\(m_{2}\),则选择\(a_{1}\);
接收者\(R\)的策略2,记为\(R(2)\):若\(S\)发出\(m_{1}\),选择 \(a_{1}\);若 \(S\)发出\(m_{2}\),则选择\(a_{2}\);
接收者\(R\)的策略3,记为\(R(3)\):若\(S\)发出\(m_{1}\),选择 \(a_{2}\);若 \(S\)发出\(m_{2}\),则选择\(a_{1}\);
接收者\(R\)的策略4,记为\(R(4)\):若\(S\)发出\(m_{1}\),选择 \(a_{2}\);若 \(S\)发出\(m_{2}\),则选择\(a_{2}\);
发送者\(S\)的纯策略中的\(S(1)\)与\(S(4)\)有一个特点,对于“自然”抽取的不同类型,\(S\)选择相同的信号,我们称具有这类特点的策略称为混同(Pooling)策略。对于\(S(2)\)与\(S(3)\),由于对不同的类型发出不同的信号,称为分离(Separating)策略。由于在这个简单情况中各种集合只有两个元素,因此博弈方的纯策略也只有混同与分离这两种,假如类型空间的元素多于两个,那么就有部分混同或准分离策略。实际上各种类型分为不同的组,对于给定的类型组中所有类型,发送者发出相同的信号:而对于不同组的类型则发生不同的信号。
在下图的博弈中当自然抽取\(t_{2}\),\(S\)在\(m_{1}\)和\(m_{2}\)这两个信号中随机选择,这样的策略称为杂合策略。这里只讨论纯策略。

由于信号博弈可以表示为完全但不完美信息动态博弈的形式,我们就可以利用精练叶斯均衡对它们进行分析。信号发送者在选择信号时知道博弈全过程,这一选择发生于单节信息集(对自然可能抽取的每一种类型都存在一个这样的信息集)。因此要求1在应用于发送者时就无需附加任何条件;如果接收者在不知道发送者类型的条件下观察到发送者的信号并选择行动,也就是说接收者的选择处于一个非单点的信息集(对发送者可能选择的每一种信号都存在一个这样的信息集,而且每一个这样的信息集中,各有一个节点对应于自然可能抽取的每一种类型)。下面我们把关于精练贝叶斯均衡要求1至要求4的事述转化为信号博弈中对精练贝叶斯均衡的要求。根据信号博弈的特点,其精练贝叶均衡的条件是:
信号要求1:(把要求1应用于 \(R\) ) 信号接收者 \(R\) 在观察到信号发出者 \(S\) 的信号后,必须有关于 \(S\) 的类型的推断,即 \(S\) 选择 \(m_j\) 时, \(S\) 是每种类型 \(t_i\) 的概率分布 \(p\left(t_i \mid m_j\right) \cdot p\left(t_i \mid m_j\right) \geq 0\) ,且 \(\sum p\left(t_i \mid m_j\right)=1\) 。
给出了信号发出方 \(S\) 信号和信号接收方 \(R\) 的推断后,再描述 \(R\) 的最优行为便十分简单。
信号要求2R:(把要求2应用于 \(R\) ) 给定 \(R\) 的判断 \(p\left(t_i \mid m_j\right)\) 和 \(S\) 的信号 \(m_j , R\) 的行为 \(a^*\left(m_j\right)\) 必须使 \(R\) 的期望得益最大,即 \(a^*\left(m_j\right)\) 是最大化问题
的解。
信号要求2S:(把要求2应用于 \(S\) ) 给定 \(R\) 的策略 \(a^*\left(m_j\right)\) 时, \(S\) 的选择 \(m^*\left(t_i\right)\) 必须使 \(S\) 的 得益最大,即 \(m^*\left(t_i\right)\) 是最大化问题
的解。
信号要求3:(把要求3、4应用于 \(R\) ) 对每个 \(m_j \in M\) ,如果存在 \(t_i \in T\) 使得 \(m^*\left(t_i\right)=m_j\) ,则 \(R\) 在对应于 \(m_j\) 的信息集处的判断必须符合 \(S\) 的策略和贝叶斯法则。即使 不存在 \(t_i \in T\) 使 \(m^*\left(t_i\right)=m_j , R\) 在 \(m_j\) 对应的信息集处的判断也仍要符合 \(S\) 的策略和贝 叶斯法则。即:
因为上述双方策略都是纯策略,因此是纯策略精练贝叶斯均衡。
3.2 企业并购中的信号传递模型
在企业并购过程中,并购双方对于并购信息的掌握是不对称的,并购企业总是处于有息不利的地位。目标企业的管理水平、产品开发能力、机构效率、投资政策、财务政策未来生产经营情况等因素将会影响企业未来的价值,但并购企业并不完全了解这些信息,因此,企业并购中存在信息不对称现象。
基本假设
(1)假定有两个时期\(T_{1}\)和\(T_{2}\),两个参与人(并购企业与目标企业)。
(2)假定目标企业在\(T_{2}\)时期的价值\(v\)服从\([0,\theta]\)上的均匀分布,目标企业知道\(\theta\) 的确切值;高质量的目标企业价值大,低质量的目标企业价值小;并购企业不知道\(\theta\),但知道目标企业属于 \(\theta\)的先验概率\(p(\theta)\)。
(3)目标企业根据自己的类型向并购企业传递信号\(x\) (我们假定目标企业发出的信号\(x\)能真实地反映目标企业的类型,不存在欺诈现象)。并购企业能从信号中推断出目标企业的预期价值水平,也就是目标企业会根据自己的真实情况向并购企业传递信息,而不是传递虚假信息。若并购企业为知情者,则其推断出目标企业的预期价值水平为 \(\beta\theta(x)\),若并购企业为未知情者,则其推断出目标企业的预期价值水平为 \(\theta(x)/2\),其中,\(x\)为目标企业发出的信号,\(\theta(x)\)为未知情的并购企业依据目标企业的信号\(x\)推断出的目标企业的最大预期价值水平。
(4)并购企业不知道目标企业的类型\(\theta\),只知道目标企业属于 \(\theta\)的概率分布\(p(\theta)\),则目标企业向并购企业发出信号\(x\) 时,并购企业根据目标企业发出的信号\(x\)推断出目标企业的预期价值水平为 \(\bar{v}(x)=\theta(x)/2\)。
(5)对于目标企业而言,其目标是最大化\(T_{1}\)时企业的价值和 \(T_{2}\) 时的预期价值水平的加权平均:
其中,\(\bar{v_{0}}(x)\) 是目标企业发出信号\(x\)时,目标企业在 \(T_{1}\)时期的价值:\(\omega\) 是\(T_{2}\)时期目标企业预期价值的权重, \(0\leq \omega \leq 1\);\(p_{s}\)为目标企业在寿命期内经营成功的概率;\(p_{1}=x/\theta\leq 1\),是目标企业在寿命期内经营失败的概率, \(p_{2}\) 为目标企业在寿命期内经营一般的概率;\(L_{1}\)是目标企业在寿合期内完全失败时道受的破产惩罚,\(L_{1} \geq 0\):\(L_{2}\)是目标企业经营一般时企业的价值, \(L_{2} \geq 0\)。
信号博弈过程
(1)“自然”选释目标企业的类型,目标金业在了解到自己的类型后,向并购企业发出关于自身企业的产品质量、投资及财务状况等方面的信号\(x\)。
(2)并购企业在观察到目标企业发出的信号\(x\)后,依据贝叶斯法则对其先验概率\(p(\theta)\)进行修正,得出后验概率$\tilde{p}\left( \theta _{i}/x_{i}\right)$,并据此判断目标企业的预期价值水平 \(\bar{v}(x)\)。
(3)目标企业知道并购企业对其发出信号的反应,因而发出最优信号值 \(x^{*}\),使自身的效用函数最大,即通过求\(max\ u(x,\bar{v}(x),\theta)\),得出 \(x\)的最优值\(x^{\ast}\)。
精练贝叶斯均衡
在信息不完全条件下,并购企业不能直接观察到目标企业的类型,因而对目标企业价值的判断只能根据所观察到的目标企业的信号\(x\)而定,此时,精练贝叶斯均衡满足:
(1)目标企业发出信号\(x\);
(2)并购企业接收到的信号\(x\)得出后验概率\(\tilde{p}=\tilde{p}\left( \theta/x\right)\),并确定对目标企业预期价值水平的评估为 \(\bar{v}(x)\),使得:
①基于目标企业的信念,给定并购企业对信号\(x\)的反应,假定目标企业的目标是最大化\(T_{1}\)时的价值和 \(T_{2}\)时的预期价值水平的加权平均,即:
②从并购企业的角度来看,并购企业对于目标企业发出信号\(x\)的反应,其目的是最大化自己的效用函数\(u_{A}\)。
③ \(\tilde{p}=\tilde{p}\left(\theta /x \right) =\frac{p\ \left( x/\theta \right) p\left( \theta \right) }{\tilde{p}\left( x\right)}\)
均衡结果分析
根据信号博弈的顺序,当目标企业选择信号\(x\)时,将预测到并购企业将据此估计目标企业的价值水平\(\bar{v}(x)=\theta(x)/2\),即并购企业认为目标企业属于类型\(\theta\)的期望是\(\theta(x)\)。考虑分离均衡:
有:
\[\begin{gathered} \frac{\partial^2 u(x, \bar{v}(x), \theta)}{\partial x \partial \theta}=\frac{\partial\left(\bar{v}_0^{\prime}(x)-\omega \cdot \bar{v}_0^{\prime}(x)-\frac{\omega}{\theta} \cdot\left(L_1+L_2\right)\right)}{\partial \theta}=\frac{\omega}{\theta^2} \cdot\left(L_1+L_2\right) \\ >0(2) \end{gathered} \]根据(2)式可以看出,价值水平 \(\theta\) 越高的目标企业,其失败的可能性越小,将 \(\bar{v}(x)=\theta(x) / 2\) 代人 (1) 式,有:
\[\begin{gathered} u(x, \bar{v}(x), \theta)=(1-\omega) \frac{\theta(x)}{2}+\omega \cdot L_2+\omega \cdot p_s(\theta) \cdot\left(\theta-L_2\right)-\omega \\ \cdot \frac{x}{\theta}\left(L_1+L_2\right) \end{gathered} \]对 (3) 式求导,得一阶条件:
\[\frac{\partial u}{\partial x}=(1-\omega) \cdot \frac{\theta^{\prime}(x)}{2}-\omega \cdot \frac{L_1+L_2}{\theta}=0 \]出现均衡时,并购企业能从目标企业发出的信号 \(x\) 正确的推断出 \(\theta\) ,即如果 \(x(\theta)\) 是属于类型 \(\theta\) 的目标企业的最好适择,则 \(\theta(x(\theta))=\theta\) ,所以 \(\frac{\partial \theta}{\partial x}=\left(\frac{\partial x}{\partial \theta}\right)^{-1}\) ,将其代入 (4) 式得:
\[2 \omega \cdot\left(L_1+L_2\right) \cdot \frac{\partial x}{\partial \theta}=(1-\omega) \cdot \theta \]求解 (5) 式得:
\[x(\theta)=\frac{1-\omega}{4 \omega \cdot\left(L_1+L_2\right)} \cdot \theta^2+C \](6) 式为目标企业经背者的均衡策略,将 \(\bar{v}(x)=\theta(x) / 2\) 代人 (6) 式,可以得到目标企线的 价值水平表达式如 (7) 式所示:
\[\bar{v}(x)=\left((x-C) \cdot \frac{\omega \cdot\left(L_1+L_2\right)}{1-\omega}\right)^{\frac{1}{2}} \]根据 (7) 式可以看出,目标企业的质量越高,价值就越大;虽然并购企业不能直接观察到目标企业的准确信息,但可以通过分析目标企业发出的信号 \(x\) 来判断目标企业真实的价值水平,从而做出正确的并购决策。