转载自:https://www.zhihu.com/tardis/bd/ans/236284413?source_id=1001
为何要引入四元数?首先是因为欧拉角有万向节死锁的问题。
3D游戏或者3D电影中,比如黑客帝国中酷炫的旋转是怎么实现的?

旋转的算法有很多,这里主要介绍其中一种:欧拉角。
1 欧拉角
1.1 欧拉角的算法思想是什么
陌生的你来到了成都,站在盐市口茫然四顾,想知道春熙路怎么走?
这个时候你选择了去问路,得到了两种回答:
- 往东经104°04′、北纬30°40′走
- 右转后一直走
第一种回答,告诉了你春熙路的绝对坐标,可是很反人类啊!
第二种回答,告诉了你春熙路的相对坐标,很具有操作性。
欧拉角算法的思想就是采用的第二种回答的方式,优点在于很好理解。
1.2 具体实现步骤
维基百科 中,有这么一副动图,清楚的表明了如何通过欧拉角来完成旋转:
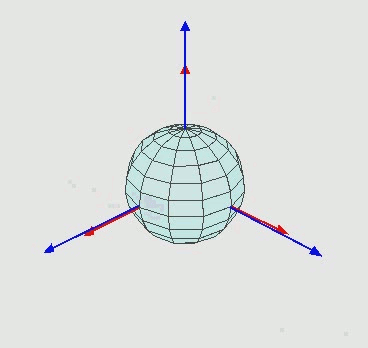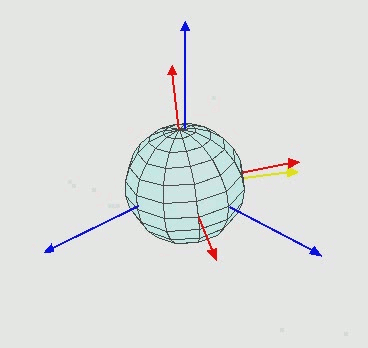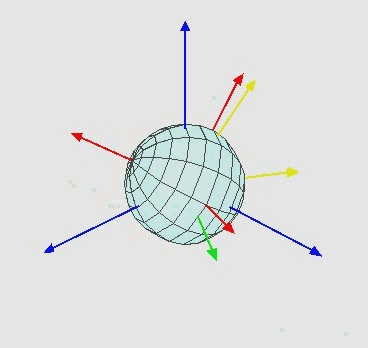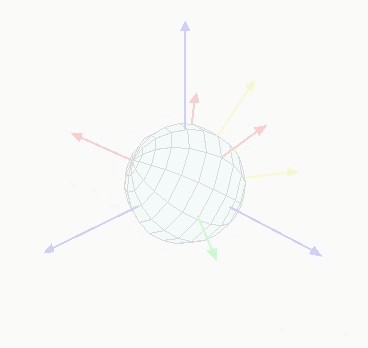
具体来拆解下旋转步骤,先看图:
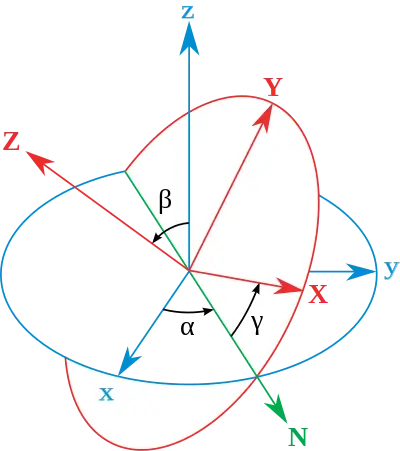
图中有两组坐标:
为全局坐标,保持不动
为局部坐标,随着物体一起运动
旋转步骤如下:
- 物体绕全局的
轴旋转
角
- 继续绕自己的
轴(也就是图中的
轴)旋转
角
- 最后绕自己的
轴旋转
角
这里有一副动图很直观的展示了旋转过程(角度标记的有点不一样: 对应
,
对应
,
对应
),图来自gfycat:

可能你感到奇怪,为什么第一步是绕着全局坐标旋转?因为要和世界保持联系,否则就和世界完全没有关系了。
还不理解?没有关系,自己动手试试(有三个可以操作的点,分别对应三个角度):
很显然,按照不同的旋转步骤,旋转的结果是不一样的。
就好比刚才问路的时候,回答你,“左转再右转”,和“右转再左转”,肯定到达的地点是不一样的。
我们需要把上面的旋转步骤按照顺序标记为 ,加上角度就是一个完整的欧拉角:
2 万向节死锁(Gimbal Lock)
局部坐标是很直观,但是导致欧拉角有一个重大缺陷,万向节死锁!
本节大部分参考了博文: 欧拉角与万向节死锁(图文版) ,博主: andrewfan 。
2.1 什么是万向节(Gimbal)
平衡环架(英语:Gimbal)为一具有枢纽的装置,使得一物体能以单一轴旋转。由彼此垂直的枢纽轴所组成的一组三只平衡环架,则可使架在最内的环架的物体维持旋转轴不变,而应用在船上的陀螺仪、罗盘、饮料杯架等用途上,而不受船体因波浪上下震动、船身转向的影响。
----维基百科
长这个样子:
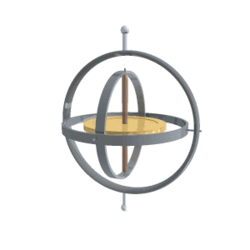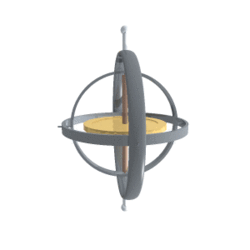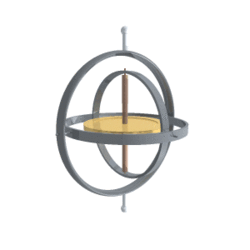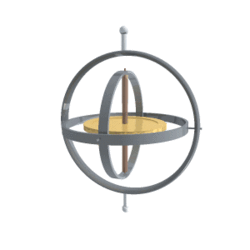
中间有一根竖轴,穿过一个金属圆盘。金属圆盘称为转子,竖轴称为旋转轴。转子用金属制成,应该是了增加质量,从而增大惯性。竖轴外侧是三层嵌套的圆环,它们互相交叉,带来了三个方向自由度的旋转。
看着不停转来转去,有点晕,接下来看下静态的。图来自百度百科:
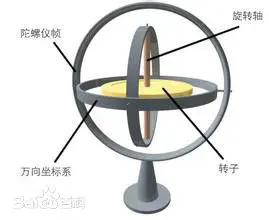
2.2 欧拉角与万向节
其实欧拉角的工作方式与万向节几乎一样。
看几幅动图就知道(图来自 Euler Angle Class )。
这个旋转叫pitch,中文是俯仰:

这个旋转叫Yaw,中文叫偏航:

这个旋转叫Roll,中文叫桶滚:

可以看出,确实工作方式和万向节一样。
2.3 死锁的产生
为了解释清楚问题,画了一个简单的万向节示意图(金属圆盘就省略了,丑点儿也就别管了):
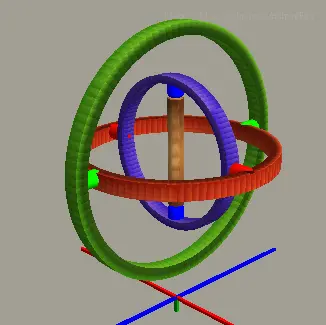
把三个Gimbal环用不同的颜色做了标记,底部三个轴向,RGB分别对应 。
假设现在这个万向节被放在一艘船上,船头的方向沿着+Z轴,也就是右前方。
2.3.1 桶滚
现在假设,船体发生了摇晃,是沿着前方进行旋转的摇晃,也就是桶滚。由于转子和旋转轴具有较大的惯性,只要没有直接施加扭矩,就会保持原有的姿态。由于上图中绿色的活动的连接头处是可以灵活转动的,此时将发生相对旋转,从而出现以下的情形:

2.3.2 俯仰
再次假设,船体发生了pitch摇晃,也就是俯仰。同样,由于存在相应方向的可以相对旋转的连接头(红色连接头),转子和旋转轴将仍然保持平衡,如下图:

2.3.3 偏航
最后假设,船体发生了yaw摇晃,也就是偏航,此时船体在发生水平旋转。相对旋转发生在蓝色连接头。如下图:

最终,在船体发生Pitch、Yaw、Roll的情况下,万向节都可以通过自身的调节,而让转子和旋转轴保持平衡。
2.3.4 死锁
现在看起来,这个万向节一切正常,在船体发生任意方向摇晃都可以通过自身调节来应对。然而,真的是这样吗?
假如,船体发生了剧烈的变化,此时船首仰起了90度(这是要翻船的节奏。。。。),此时的陀螺仪调节状态如下图:
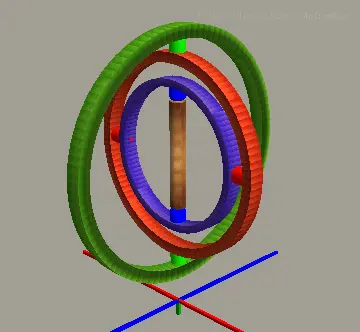
此时,船体再次发生转动,沿着当前世界坐标的+Z轴(蓝色轴,应该正指向船底)进行转动,那么来看看发生了什么情况:

现在,转子不平衡了,万向节的三板斧不起作用了。它失去了自身的调节能力。那么这是为什么呢?
之前万向节之所以能通过自身调节,保持平衡,是因为存在可以相对旋转的连接头。在这种情况下,已经不存在可以相对旋转的连接头了。
那么连接头呢?去了哪里?显然,它还是在那里,只不过从上图中,我们清楚地看到:
- 红色连接头:可以给予一个相对俯仰的自由度。
- 绿色连接头:可以给予一个相对偏航的自由度。
- 蓝色连接头:可以给予一个相对偏航的自由度。
没错,三个连接头,提供的自由度只对应了俯仰和偏航两个自由度,桶滚自由度丢失了。
我们可以回头去试试之前的 操作页面 ,在下面这样子的情况下其实就是死锁了:
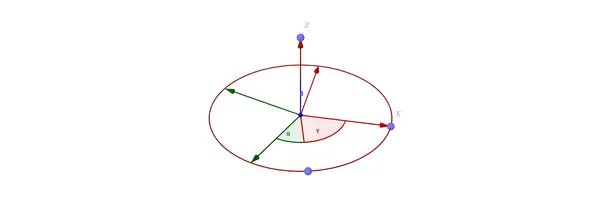
4 总结
在编程中很难规避死锁问题,所以现在很多时候都使用四元数实现旋转,四元数那又是另外的话题了。