完全信息静态博弈是指参与者在做出决策之前拥有所有可能的信息,包括对手的策略和利益。因此,每位参与者可以准确地评估各种选择对自己和对手的影响。这种情况下,决策的结果是确定性的,不受随机因素影响。参与者通过理性分析和预测对手的行为,以最大化自身利益。完全信息静态博弈广泛应用于经济、政治和生活中的决策情境,帮助人们理解和优化策略选择,从而达到最佳的个人或集体结果。

一、博弈的策略式
参与人(Players): \(N\)参与人的集合;第\(i\)参与人。
博弈参与人的策略集(Strategy sets):\(S_i\)参与人的策略集,\(s_i\)参与人策略集的一个元素。所有参与人的策略放在一起,称之为博弈的策略组合,表示为\(S = (s_1, s_2, … ,s_n)\)。
博弈参与人的支付函数(Payoff): \(u_i\)参与人\(i\)的支付函数\(i\in N\);\(u_i(s_1,s_2,...,s_i,...,s_n)\)。
博弈的策略式可用收益矩阵来直观表示,见下图。

二、占优策略(Dominant Strategies)
在完全信息静态博弈中,由于信息完全、参与人同时行动,所以恰好用博弈的策略式描述其模型,又由于参与人有限,所以博弈的策略式可去掉参与人集合,简化为\(G = \{\{ S_i \}_{i=1}^N, \{ u_i \}_{i=1}^N \}\) ,\(|N|=n\)。
在博弈$$G=\{S_1,S_2,S_3,...,S_n;u_1,u_2,...u_n\}$$中,如果\(s_i^{'}\)和\(s_i^{''}\)代表的参与者\(i\)的两个策略,如果对于其他的参与者每一个可能的策略组合,\(i\)选择\(s_i^{'}\)的收益都小于选择\(s_i^{''}\)的收益,则称策略\(s_i^{'}\)相对于策略\(s_i^{''}\)是严格劣策略,即
对其他参与者在其战略空间 \(S_1,\cdot\cdot\cdot,S_{i-1},S_{i+1},\cdot\cdot\cdot,S_n\)中每一组可能的策略组合 \((s_1,\cdot\cdot\cdot,s_{i-1},s_{i+1},\cdot\cdot\cdot,s_n)\) 都成立。
同样,若\(s_i^{'}\)和\(s_i^{''}\)代表的参与者\(i\)的两个策略,如果对于其他的参与者每一个可能的策略组合,\(i\)选择\(s_i^{'}\)的收益都大于选择\(s_i^{''}\)的收益,则称策略\(s_i^{'}\)相对于策略\(s_i^{''}\)是严格优策略,即
\[u_i(s_1,s_2,...,s_{i-1},s_i^{'},s_{i+1},..,s_n)>u_i(s_1,s_2,...,s_{i-1},s_i^{''},s_{i+1},..,s_n) \]对其他参与者在其策略空间 \(S_1,\cdot\cdot\cdot,S_{i-1},S_{i+1},\cdot\cdot\cdot,S_n\)中每一组可能的策略组合\((s_1,\cdot\cdot\cdot,s_{i-1},s_{i+1},\cdot\cdot\cdot,s_n)\) 都成立。
若上面关系变为
则称策略\(s_i^{'}\)相对于策略\(s_i^{''}\)是弱劣策略,反之就是弱优策略。
理性的参与者不会选择严格劣战略,因为他对其他的人的选择没有办法判断,所以这一个战略是他的最优反应。
占优策略:若\(s_i^{'}\)参与者\(i\)的一个策略,如果对于其他参与者每一个可能的策略组合,\(i\)选择\(s_i^{'}\)的收益都大于或等于选择\(s_i\)的收益,其中\(s_i\)是\(S_i\)任一策略,则称策略\(s_i^{'}\)是参与人\(i\)的占优策略,即
对其他参与者在其策略空间 \(S_1,\cdot\cdot\cdot,S_{i-1},S_{i+1},\cdot\cdot\cdot,S_n\)中每一组可能的策略组合\((s_1,\cdot\cdot\cdot,s_{i-1},s_{i+1},\cdot\cdot\cdot,s_n)\) ,对任一\(s_i \in S_i\)均成立。
占优策略:是指不论对手选择什么,自己的某个策略都不比其他策略差的策略。如果自己的某个策略严格强于(收益大于)任何其他策略,那么该策略还被称为严格占优策略。占优均衡:如果每个参与人都存在占优策略,那么这些占优策略放在一起,构成了博弈的占优均衡。劣策略:是指不论对手选择什么,自己都不会选择的策略。对于劣策略。可以直接剔除以简化博弈,如果剔除到最后只留下唯一一个策略组合,那么这个策略组合就是我们说的重复剔除严格劣策略均衡。如果存在重复剔除严格劣策略均衡,那么我们说这个博弈是重复剔除劣策略可解的。
【例1】考虑下面的囚徒困境博弈
| 坦白 | 抵赖 | |
|---|---|---|
| 坦白 | -8,-8 | 0,-10 |
| 抵赖 | -10,0 | -1,-1 |
对于选择坦白,对手无论是坦白或者抵赖,选择坦白的结果均好于抵赖,可知,坦白属于占优策略,(-8,-8)称为占优策略均衡。
【例2】考虑下面的博弈(重复剔除严格劣策略)
| 参与人2 | ||||
| 左 | 中 | 右 | ||
| 参与人1 | 上 | 1,0 | 1,2 | 0,1 |
| 下 | 0,3 | 0,1 | 2,0 |
分析上述例子,如果参与人1选择上,参与人2会选择中;如果参与人1选择下,参与人2会选择左,所以战略右就是参与人2的严格劣策略,则上述博弈变为:
| 参与人2 | |||
| 左 | 中 | ||
| 参与人1 | 上 | 1,0 | 1,2 |
| 下 | 0,3 | 0,1 |
如果参与人2选择左,参与人1会选择上;如果参与人2选择中,则参与人1会选择上,所以策略(下)就是参与人1的严格劣策略,则上述博弈变为:
| 参与人2 | |||
| 左 | 中 | ||
| 参与人1 | 上 | 1,0 | 1,2 |
如果参与人1选择上,则参与人2会选择中,所以策略左就是参与人2的严格劣策略,则上述博弈的最终结果就是(上,中):
| 参与人2 | ||
| 中 | ||
| 参与人1 | 上 | 1,2 |
【例3】考虑下面的博弈(重复剔除严格劣策略)
| Player1, Player2 | a | b |
|---|---|---|
| A | 3,4 | 4,3 |
| B | 5,3 | 3,5 |
| C | 5,3 | 4,3 |
本例中不存在严格劣策略,则考虑重复剔除弱劣策略。对于Player1, 策略A、B弱劣于C,所以去掉收益矩阵的第一、二行,得
| Player1, Player2 | a | b |
|---|---|---|
| C | 5,3 | 4,3 |
最后均衡的选择取决于Player2的策略选择。
二、纳什均衡
我们自然地会去想,在这种条件下,两个囚犯会选择怎样的策略呢?先从A的视角想一下,
- 如果B坦白:A选择坦白,收益是(-6);A选择沉默,收益是(-12),因此A会坦白。
- 如果B沉默:A选择坦白,收益是(0);A选择沉默,收益是(-1),因此A会坦白。
同理,B也是这么想的,因此,两人都会选择坦白。
1. 纳什均衡的想法
从上面的思考中,可以看出这种思想:当对手策略选定的时候,我会调整自己的策略,使得自己收益在几种策略选择中是最大的,这时的策略称为“最优反应”。这个时候,如果对手不改变策略的话,我是没有动机去改变自己的策略的。
如果每个人的策略都是“最优反应”,那么就会形成一种稳定的局面,这时的博弈结果就是纳什均衡
2. 纳什均衡形式化定义
纳什均衡(Nash equilibrium)是博弈结果a∗=(a1∗,a2∗,…,aN∗)a{*}=\left(a_{1}, a_{2}^{*}, \ldots, a_{N}{*}\right)a=\left(a_{1}^{*}, a_{2}^{*}, \ldots, a_{N}^{*}\right),使得对于每个玩家iii都有: ui(ai∗,a−i∗)≥ui(ai,a−i∗) u_{i}\left(a_{i}^{*}, a_{-i}^{*}\right) \geq u_{i}\left(a_{i}, a_{-i}^{*}\right) \\ u_{i}\left(a_{i}^{*}, a_{-i}^{*}\right) \geq u_{i}\left(a_{i}, a_{-i}^{*}\right) \\ (对手策略选定的时候,自己最优)
纳什均衡简写为:NE
3. 纳什均衡求解:寻找最优反应
玩家iii关于对手策略a−ia_{-i}a_{-i}的最优反应:Bi(a−i)={ai∈Ai:ui(ai,a−i)≥ui(bi,a−i) for all bi∈Ai}B_{i}\left(a_{-i}\right)=\left\{a_{i} \in A_{i}: u_{i}\left(a_{i}, a_{-i}\right) \geq u_{i}\left(b_{i}, a_{-i}\right) \text { for all } b_{i} \in A_{i}\right\}B_{i}\left(a_{-i}\right)=\left\{a_{i} \in A_{i}: u_{i}\left(a_{i}, a_{-i}\right) \geq u_{i}\left(b_{i}, a_{-i}\right) \text { for all } b_{i} \in A_{i}\right\}
同时满足所有人的最优反应的博弈结果,就是纳什均衡。也就是对于 ∀i\forall i\forall i ,满足ai∗∈Bi(a−i∗)a_{i}^{*} \in B_{i}\left(a_{-i}{*}\right)a_{i} \in B_{i}\left(a_{-i}^{*}\right)的博弈结果。
4. 例1:依旧是囚徒困境

B1(c)={c}B1(d)={c}B2(c)={c}B2(d)={c} \begin{array}{ll} B_{1}(c)=\{c\} & B_{1}(d)=\{c\} \\ B_{2}(c)=\{c\} & B_{2}(d)=\{c\} \end{array} \\ \begin{array}{ll} B_{1}(c)=\{c\} & B_{1}(d)=\{c\} \\ B_{2}(c)=\{c\} & B_{2}(d)=\{c\} \end{array} \\ 在收益矩阵上标出这些最优反应:


B1(c)={c}B_1(c)=\{c\}B_1(c)=\{c\}表示在囚徒2选择c的时候,囚徒1会选择c,因为囚徒1的收益(-6 > -12)。对应矩阵中左边红色的”√“。
详细分析如下:
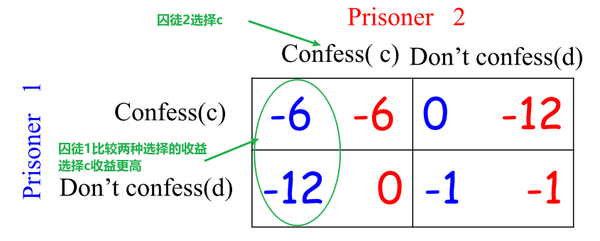
B1(d)={c}B_1(d)=\{c\}B_1(d)=\{c\}表示在囚徒2选择d的时候,囚徒1会选择c,因为囚徒1的收益(0 > -1)。对应矩阵中右边红色的”√“。
B2(c)={c}B_2(c)=\{c\}B_2(c)=\{c\}表示在囚徒1选择c的时候,囚徒2会选择c,因为囚徒2的收益(-6 > -12)。对应矩阵中上边绿色的”√“。
B2(d)={c}B_2(d)=\{c\}B_2(d)=\{c\}表示在囚徒1选择d的时候,囚徒2会选择c,因为囚徒2的收益(0 > -1)。对应矩阵中下边绿色的”√“。
因此,最终得到满足所有人最优反应的结果:(c,c),也就是两人都坦白。
5. 例2:古诺竞争
这个例子收益是连续的,不能用矩阵来表示。问题如下:
两个厂商{1, 2}生产和销售同一种商品,厂商iii生产的数量记为qiq_iq_i。 每件商品生产成本都是c,售价是:max(0,a−b(q1+q2))max(0,a-b(q_1+q_2))max(0,a-b(q_1+q_2)) 求纳什均衡
1) 形式化
G={{1,2},{q1,q2},{u1,u2}}G = \{\{1,2\}, \{ q_1,q_2 \}, \{ u_1,u_2 \} \}G = \{\{1,2\}, \{ q_1,q_2 \}, \{ u_1,u_2 \} \}
其中,收益ui(q1,q2)=(max(0,a−b(q1+q2))−c)qiu_i(q_1,q_2) = (max(0,a-b(q_1+q_2))-c)q_iu_i(q_1,q_2) = (max(0,a-b(q_1+q_2))-c)q_i。(售价-成本)x生产数量
2) 求最优反应函数
对于厂商1:
- 如果q2≥(a−c)/bq_{2} \geq(a-c) / bq_{2} \geq(a-c) / b,那么对于任意的q1≥0q_1 \ge 0q_1 \ge 0,都有u1(q1,q2)≤0u_{1}\left(q_{1}, q_{2}\right) \leq 0u_{1}\left(q_{1}, q_{2}\right) \leq 0,即没有正收益
- 如果q2<(a−c)/bq_{2} < (a-c) / bq_{2} < (a-c) / b,那么u1(q1,q2)=(a−b(q1+q2))−c)q1u_1(q_1,q_2) = (a-b(q_1+q_2))-c)q_1u_1(q_1,q_2) = (a-b(q_1+q_2))-c)q_1。
- 固定q2q_2q_2,q1q_1q_1何时取最大呢?求导!
- 求解:∂u1(q1,q2)∂q1=a−c−bq2−2bq1=0\frac{\partial u_{1}\left(q_{1}, q_{2}\right)}{\partial q_{1}}=a-c-b q_{2}-2 b q_{1}=0 \frac{\partial u_{1}\left(q_{1}, q_{2}\right)}{\partial q_{1}}=a-c-b q_{2}-2 b q_{1}=0 ,求得q1=(a−c−bq2)/2bq_{1}=\left(a-c-b q_{2}\right) / 2 bq_{1}=\left(a-c-b q_{2}\right) / 2 b,这就是厂商1的最优反应函数
同理,对于厂商2,最优反应函数是:q2=(a−c−bq1)/2bq_{2}=\left(a-c-b q_{1}\right) / 2bq_{2}=\left(a-c-b q_{1}\right) / 2b
3) 纳什均衡
对于满足纳什均衡的博弈结果(q1∗,q2∗)\left(q_{1}^{*}, q_{2}{*}\right)\left(q_{1}, q_{2}^{*}\right),有: q1∗=B1(q2∗)=(a−c−bq2∗)/2bq2∗=B2(q1∗)=(a−c−bq1∗)/2b \begin{array}{l} q_{1}{*}=B_{1}\left(q_{2}\right)=\left(a-c-b q_{2}^{*}\right) / 2 b \\ q_{2}{*}=B_{2}\left(q_{1}\right)=\left(a-c-b q_{1}^{*}\right) / 2 b \end{array} \\ \begin{array}{l} q_{1}{*}=B_{1}\left(q_{2}\right)=\left(a-c-b q_{2}^{*}\right) / 2 b \\ q_{2}{*}=B_{2}\left(q_{1}\right)=\left(a-c-b q_{1}^{*}\right) / 2 b \end{array} \\ 联立方程,解得q1∗=q2∗=a−c3bq_{1}^{*}= q_{2}{*}=\frac{a-c}{3b}q_{1}= q_{2}^{*}=\frac{a-c}{3b}
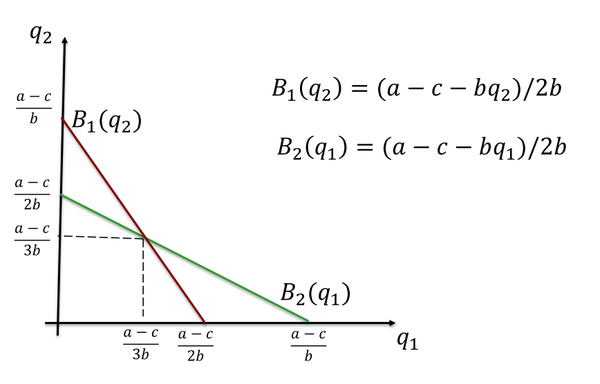
最优反应相交之处
三、实例
总结
完全信息静态博弈在市场竞争、定价策略、合作与竞争等经济决策中发挥重要作用。在企业在制定定价、推广、市场份额等策略时,需要考虑竞争对手的决策,这就涉及到博弈的思维;政治家和政府在制定政策、谈判协议时,需要考虑其他国家或政治实体的反应,这也涉及到博弈理论;国际间的环境协议,如气候变化协定,涉及到各国在资源分配上的博弈。
完全信息静态博弈提供了对决策情境的深入理解,帮助人们预测他人可能的行为,并做出更明智的选择。它强调了理性决策者如何在已知信息的基础上优化自己的利益。然而,博弈理论在现实中可能会受到信息不对称、非理性行为和多方利益等因素的影响,因此在实际应用中需要综合考虑更多的因素。尽管如此,完全信息静态博弈仍然为许多领域的决策提供了有益的分析框架。