Sobolev空间初探2
2.2 逼近
2.2. 1 局部逼近
现在我们考虑用光滑函数逼近Sobolev 函数, 这里逼近的基本思想就是对函数进行磨光.
引理 10. (局部逼近) 设 \(\Omega_{\varepsilon}=\{x \in \Omega \mid \operatorname{dist}(x, \partial \Omega)>\varepsilon\}\), 设 \(\mathrm{h}\) 函数 \(u \in W_{\mathrm{loc}}^{1, p}(\Omega)\), 则对任意的 \(\varepsilon>0\), 都有 \(J_{\varepsilon} u \in C^{\infty}\left(\Omega_{\varepsilon}\right)\), 并且对任意的开集 \(\Omega^{\prime} \Subset \Omega\), 当 \(\varepsilon \rightarrow 0\) 时, 有:
\[\begin{aligned} & \int_{\Omega^{\prime}}\left|J_{\varepsilon} u(x)-u(x)\right|^{p} \mathrm{~d} \mathrm{x} \rightarrow 0 \\ & \int_{\Omega^{\prime}}\left|D^{\alpha}\left(J_{\varepsilon} u(x)\right)-D^{\alpha} u(x)\right|^{p} \mathrm{dx} \rightarrow 0 \end{aligned} \]证明:首先做一个说明, 这里的 \(J_{\varepsilon}\) 是我们常见的磨光子. 令 \(\varepsilon<\operatorname{dist}\left(\Omega^{\prime}, \partial \Omega\right)=d>0, x \in \Omega^{\prime}\)
\[\begin{aligned} J_{\varepsilon} u(\boldsymbol{x}) & =\varepsilon^{-n} \int_{\Omega} \rho\left(\frac{\boldsymbol{x}-\boldsymbol{y}}{\varepsilon}\right) u(\boldsymbol{y}) \mathrm{d} \boldsymbol{y} \\ & =\varepsilon^{-n} \int_{|\boldsymbol{x}-\boldsymbol{y}|<\varepsilon} \rho\left(\frac{\boldsymbol{x}-\boldsymbol{y}}{\varepsilon}\right) u(\boldsymbol{y}) \mathrm{d} \boldsymbol{y} \\ & =\int_{|\boldsymbol{z}|<1} \rho(\boldsymbol{z}) u(\boldsymbol{x}-\boldsymbol{\varepsilon} \boldsymbol{z}) \mathrm{d} \boldsymbol{z} \end{aligned} \]同时注意到: \(u(x)=\int_{|z|<1} \rho(z) u(x) \mathrm{d} z\), 这是因为 \(\int_{|z|<1} \rho(z) \mathrm{d} z=1\), 因此我们就有:
\[J_{\varepsilon} u(x)-u(x)=\int_{|z|<1} \rho(z)(u(x-\varepsilon z)-u(x)) \mathrm{d} z \]因此我们记有:
\[\left\|J_{\varepsilon} u-u\right\|_{L^{p}\left(\Omega^{\prime}\right)} \leqslant \int_{|z|<1} \rho(z)\|u(x-\varepsilon z)-u(x)\|_{L^{p}\left(\Omega^{\prime}\right)} \mathrm{d} z \]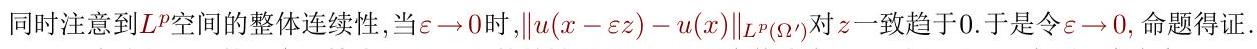
现在我们证明第二个不等式,这里证明的关键: \(D^{\alpha}\) 可以和 \(J_{\varepsilon}\) 交换次序.这里我们需要注意到一个事实:
\[D_{x}^{\alpha} \rho(x-y)=(-1)^{|\alpha|} D_{y}^{\alpha} \rho(x-y) \]因此我们有:
\[\begin{aligned} D^{\alpha} u_{\varepsilon}(x) & =\frac{1}{\varepsilon^{n}} \int_{U} D_{x}^{\alpha} \rho\left(\frac{x-y}{\varepsilon}\right) u(y) d y \\ & =(-1)^{|\alpha|} \frac{1}{\varepsilon^{n}} \int_{U} D_{y}^{\alpha} \rho\left(\frac{x-y}{\varepsilon}\right) u(y) d y \\ & =\frac{1}{\varepsilon^{n}} \int_{U} \rho\left(\frac{x-y}{\varepsilon}\right) D_{y}^{\alpha} u(y) d y \\ & =J_{\varepsilon}\left(D^{\alpha} u\right) \end{aligned} \]现在等价于证明:
由于 \(D^{\alpha} u \in L_{\mathrm{loc}}^{p}\), 故定理得证.
\[\int_{\Omega^{\prime}}\left|\left(J_{\varepsilon} D^{\alpha} u(x)\right)-D^{\alpha} u(x)\right|^{p} \mathrm{dx} \rightarrow 0 \]这个引理等价:
引理. 设 \(u \in W^{k, p}(\Omega)\), 其中 \(1 \leq p<\infty\), 则对于任意的 \(V \subset \subset \Omega\), 存在光滑函数列在 \(W^{k, p}(V)\) 中逼近 \(u\), 即:
\[\left\|u_{m}-u\right\| \rightarrow 0, u_{m}, u \in W^{k, p}(V) \]2.2.2 内部逼近
借助我们前边建立的局部逼近定理,我们可以借助单位分解定理证明内部逼近定理.
定理 11. (内部逼近) 设 \(u \in W^{k, p}(\Omega)\), 其中 \(1 \leq p<\infty\), 存在函数列 \(u_{k} \in W^{k, p}(\Omega) \cap C^{\infty}(\Omega)\) 中逼近 \(u\), 即:
\[\left\|u_{m}-u\right\|_{W^{k, p}} \rightarrow 0, u_{m}, u \in W^{k, p}(\Omega) \]证明: 定义开集 \(\Omega_{0}=\varnothing, \Omega_{i}=\left\{\boldsymbol{x} \in \Omega\left|\operatorname{dist}(\boldsymbol{x}, \partial \Omega) > \frac{1}{i},\right| \boldsymbol{x} \mid < i\right\}\), 显然 \(\Omega=\bigcup_{i=0}^{\infty}\left(\Omega_{i+2}-\bar{\Omega}_{i}\right)=\left(\Omega_{2}-\bar{\Omega}_{0}\right) \cup\left(\Omega_{3}-\bar{\Omega}_{1}\right) \cup \cdots\) 任一紧集 \(K \subset \Omega\) 仅与有限个开集 \(\Omega_{i+2}-\bar{\Omega}_{i}\) (记为 \(\left.V_{i}\right)\) 相交. 由单位分解定理知存在相应的单位分解:
\[\alpha_{i} \in C_{0}^{\infty}\left(V_{i}\right), \sum_{i=0}^{\infty} \alpha_{i}=1, x \in \Omega \]因此: \(u=\sum \alpha_{i} u=\sum u_{i}\). 同时注意到对每个 \(\Omega\) 中的紧集 \(K\), 它至多和有限个 \(V_{i}\) 相交 .
根据局部逼近定理我们知道, 当 \(\varepsilon_{i}\) 充分小时:
\[\operatorname{supp}\left(J_{\varepsilon_{i}} u_{i}\right) \subset V_{i} \quad,\left\|J_{\varepsilon_{i}} u_{i}-u\right\|_{W^{k, p}}<\frac{\varepsilon}{2^{i+1}} \]记 \(w=\sum J_{\varepsilon_{i}} u_{i}\). 由于每个紧集 \(K\) 至多和有限个 \(\operatorname{supp}\left(J_{\varepsilon_{i}} u_{i}\right)\) 相交, 因此 \(w \in C^{\infty}(\Omega)\), 由 Minkowski不等式, 我们可以得到:
\[\begin{aligned} \|w-u\|_{k, p, \Omega} & =\left\|\sum_{i=0}^{\infty} J_{\varepsilon_{i}}\left(u \alpha_{i}\right)-\sum_{i=0}^{\infty} u \alpha_{i}\right\|_{k, p, \Omega} \\ & \leqslant \sum_{i=0}^{\infty}\left\|J_{\varepsilon_{i}}\left(u \alpha_{i}\right)-u \alpha_{i}\right\|_{k, p, \Omega} \\ & \leqslant \sum_{i=0}^{\infty} \frac{\varepsilon}{2^{i+1}}=\varepsilon . \end{aligned} \]因此定理得证.
2.3.3 边界光滑逼近
现在我们要提问,能否找到 \(u \in C^{\infty}(\bar{\Omega})\) 取逼近 \(W^{m, p}\) 中的函数.此时我们就需要对边界提出一些要求.
我们先考察边界是平展的情况.
引理 12. 如果 \(u \in W_{p}^{k}\left(\mathbb{R}_{+}^{n}\right)\), 那么存在 \(u_{j} \in C^{\infty}\left(\overline{\mathbb{R}_{+}^{n}}\right)\), 在 \(W^{k, p}\left(\mathbb{R}_{+}^{n}\right)\) 中 \(u_{j} \longrightarrow u\). 这里, \(\overline{\mathbb{R}_{+}^{n}}=\left\{x \in \mathbb{R}^{n}: x_{n} \geqslant 0\right\}\).
证明: 对 \(u \in W^{k, p}\), 我们定义 \(u_{\eta}(x):=u\left(x^{\prime}, x_{n}+\eta\right), x^{\prime}=\left(x_{1}, \cdots, x_{n-1}\right)\). 这里显然只要 \(x_{n}+\eta>0, u_{\eta}\) 就有意义. 由 \(L^{p}\) 的整体连续性我们知道:
\[\left\|u_{\eta}-u\right\|_{k, p} \rightarrow 0, \eta \rightarrow 0^{+} \]现在对 \(u_{\eta}\) 进行磨光, 就得到了 \(J_{\varepsilon} u_{\eta}\), 只要 \(\varepsilon<\frac{\eta}{2}\), 我们就得到了:
\[J_{\varepsilon} u_{\eta} \in C^{\infty}\left(\left\{y_{n}>-\frac{\eta}{2}\right\}\right),\left\|J_{\varepsilon} u_{\eta}-u_{\eta}\right\|_{k, p} \rightarrow 0 \]因此我们就有:
\[\left\|J_{\varepsilon} u_{\eta}-u\right\|_{k, p} \leqslant\left\|J_{\varepsilon} u_{\eta}-u_{\eta}\right\|_{k, p}+\left\|u_{\eta}-u\right\|_{k, p} \rightarrow 0 \]现在令 \(\varepsilon=\frac{1}{k}, \eta=\frac{3}{k}, u_{k}=J_{\frac{1}{k}} u_{3}\). 于是定理得证.
这里就可以观察到, 这里证明的关键在于构造了 \(u_{\eta}\) 这样的函数, 以及 \(u_{\eta}\) 所具有的良好性质, 这都离不开区域在边界具有某种可以平移的良好性质.
定理 13. 如果 \(\Omega\) 有界并且 \(\partial \Omega \in C^{m}, u \in W^{m, p}(\Omega)\), 那么存在 \(u_{m} \in C^{\infty}(\bar{\Omega})\), 在 \(W^{m, p}(\Omega)\) 中 \(u_{m} \longrightarrow u\).
分析: 证明的基本思想就是先局部化, 利用边界的光滑性质将其变为展平, 对展平的函数找到逼近函数, 再返回到原来的边界, 利用单位分解定理将所得函数拼起来得到 整体光滑的函数.
证明: (1): 由于边界是有界的, 因此首先利用开覆盖定理, 就可以找到有限个开球覆盖边界 \(\left\{O_{i}\right\}_{i=1}^{N}\), 利用变换 \(y=\phi_{i}(x)\) 将边界映到 \(\mathbb{R}^{n}\) 使得:
\[\phi_{i}\left(O_{i}\right)=B_{1}(0), \phi_{i}\left(\Omega \cap O_{i}\right)=B_{1}^{+}(0), \phi_{i}\left(\partial \Omega \cap O_{i}\right)=\left\{y_{n}=0\right\} \cap B_{1}(0) \]我们再取 \(O_{0} \Subset \Omega\), 使得 \(\Omega \subset \bigcup_{i=0}^{n} O_{i}\). 因此有从属于该开覆盖的单位分解 \(\alpha_{i} \in C_{0}^{\infty}\left(O_{i}\right), \sum_{i=0}^{N} \alpha_{i}(\boldsymbol{x})=1, \boldsymbol{x} \in \Omega\), 令:
\[u=u \sum_{i=0}^{N} \alpha_{i}=\sum_{i=0}^{N} u \alpha_{i}=\sum_{i=1}^{N} u_{i}, \quad u_{i}=u \alpha_{i} \]这里的局部有限性导致了对于任意的 \(x_{0} \in K \subset \subset \Omega\), 求和只能是有限个. 由弱导数的性质 4 , 我们知道 \(u_{i} \in W^{k, p}\left(O_{i}\right)\), 将其进行零延拓就得到 \(u_{i} \in W^{k, p}\left(\mathbb{R}^{n}\right)\). 由于 \(O_{0}\) 不包含边界, 因此直接利用局部逼近定理就可以得到存在 \(u_{\mathrm{ok}} \in C_{0}^{\infty}\left(\mathbb{R}^{n}\right)\) 逼近 \(u_{0}\).
(2): 现在我们讨论边界上的情况. 首先我们证明一个引理:
引理 14. 记号同上. 设 \(u_{i} \in W^{1, p}\left(O_{i} \cap \Omega\right)\), 记函数 \(u_{i}(x)=u_{i}\left(\phi_{i}^{-1}(y)\right)=v(y)\). 现在我们证明 \(v(y) \in W^{1, p}\left(B_{1}^{+}(0)\right)\), 并且链式法则成立:
\[\frac{\partial v_{i}}{\partial y_{k}}=\frac{\partial u_{i}}{\partial x_{l}} \frac{\partial x_{l}}{\partial y_{k}}, \quad \frac{\partial u_{i}}{\partial x_{l}}=\frac{\partial v_{i}}{\partial y_{k}} \frac{\partial y_{k}}{\partial x_{l}} \]并且有如下等价范数:
\[C^{-1}|| v_{i}\left\|_{1, p, B_{1}^{+}(O)} \leqslant\right\| u_{i}\left\|_{1, p, \Omega \cap O_{i}} \leqslant C \mid\right\| v_{i} \|_{1, p, B_{1}^{+}(O)} \]证明: 证明的基本思想是利用光滑函数逼近定理. 由于 \(u_{i} \in W^{1, p}\), 因此存在光滑函数 \(u_{\mathrm{ih}} \in C^{\infty}\left(O_{i} \cap \Omega\right)\) 逼近 \(u_{i}\). 我们记 \(v_{\mathrm{ih}}\) 是对应复和函数, 则光滑函数的链式法则是成立
\[\frac{\partial v_{i h}}{\partial y_{k}}(\boldsymbol{y})=\frac{\partial u_{i h}}{\partial x_{l}}\left(\phi^{-1}(\boldsymbol{y})\right) \frac{\partial x_{l}(\boldsymbol{y})}{\partial y_{k}}, \quad \frac{\partial u_{i h}}{\partial x_{l}}(\boldsymbol{x})=\frac{\partial v_{i h}}{\partial y_{k}}(\phi(\boldsymbol{x})) \frac{\partial y_{k}(\boldsymbol{x})}{\partial x_{l}} \]因此对应任意的 \(\varphi(y) \in C_{0}^{\infty}\left(B_{1}^{+}(0)\right)\), 有:
\[-\int_{B_{1}^{+}(O)} v_{i h}(\boldsymbol{y}) \frac{\partial \varphi_{1}}{\partial y_{k}}(\boldsymbol{y}) \mathrm{d} \boldsymbol{y}=\int_{B_{1}^{+}(O)} \frac{\partial u_{i h}}{\partial x_{l}}\left(\phi^{-1}(\boldsymbol{y})\right) \frac{\partial x_{l}(\boldsymbol{y})}{\partial y_{k}} \varphi_{1}(\boldsymbol{y}) \mathrm{d} \boldsymbol{y} \]作逆变换:
\[-\int_{\Omega \cap O_{i}} u_{i h}(\boldsymbol{x}) \frac{\partial \varphi_{1}}{\partial y_{k}}(\phi(\boldsymbol{x}))\left|\frac{\partial \boldsymbol{y}(\boldsymbol{x})}{\partial \boldsymbol{x}}\right| \mathrm{d} \boldsymbol{x}=\int_{\Omega \cap O_{i}} \frac{\partial u_{i h}}{\partial x_{l}}(\boldsymbol{x}) \frac{\partial x_{l}}{\partial y_{k}}(\phi(\boldsymbol{x})) \varphi_{1}(\phi(\boldsymbol{x}))\left|\frac{\partial \boldsymbol{y}(\boldsymbol{x})}{\partial \boldsymbol{x}}\right| \mathrm{d} \boldsymbol{x} \]由于 \(L^{p}\) 中的强收敛蕴含弱收敛, 因此当 \(h \rightarrow 0\) 时, 极限可以取进去, 于是就有:
\[-\int_{\Omega \cap O_{i}} u_{i}(\boldsymbol{x}) \frac{\partial \varphi_{1}}{\partial y_{k}}(\phi(\boldsymbol{x}))\left|\frac{\partial \boldsymbol{y}(\boldsymbol{x})}{\partial \boldsymbol{x}}\right| \mathrm{d} \boldsymbol{x}=\int_{\Omega \cap O_{i}} \frac{\partial u_{i}}{\partial x_{l}}(\boldsymbol{x}) \frac{\partial x_{l}}{\partial y_{k}}(\phi(\boldsymbol{x})) \varphi_{1}(\phi(\boldsymbol{x}))\left|\frac{\partial \boldsymbol{y}(\boldsymbol{x})}{\partial \boldsymbol{x}}\right| \mathrm{d} \boldsymbol{x} \]再次逆回去.
\[-\int_{B_{1}^{+}(O)} v_{i}(\boldsymbol{y}) \frac{\partial \varphi_{1}}{\partial y_{k}}(\boldsymbol{y}) \mathrm{d} \boldsymbol{y}=\int_{B_{1}^{+}(O)} \frac{\partial u_{i}}{\partial x_{l}}\left(\phi^{-1}(\boldsymbol{y})\right) \frac{\partial x_{l}}{\partial y_{k}}(\boldsymbol{y}) \varphi_{1}(\boldsymbol{y}) \mathrm{d} \boldsymbol{y} \]至于范数的等价性我们在数学分析中已经熟悉了.这里频繁的逆变换是因为我们并不清楚变换到 \(B_{1}^{+}(0)\) 的函数有什么样的性质, 因此做什么都只能在原来的积分做好了再变回去.
(3): 回到原定理的证明.
由于 \(v_{i} \in W^{k, p}\left(B_{1}^{+}(0)\right)\) 在 \(B_{1}^{+}(0)\) 具有紧支集因此我们将其进行零延拓之后 \(v_{i} \in W^{k, p}\left(\mathbb{R}^{n}\right)\). (记为 \(\left.\tilde{v}_{i}\right)\). 并且我们知道 \(\operatorname{spt}\left(v_{i}\right) \subset B_{1}^{+}(0)\), 且 \(\operatorname{spt}\left(\tilde{v}_{i}\right) \subset \overline{B_{1}^{+}}\). 由引理 12 知存在 \(\tilde{v}_{i k} \in C^{\infty}\left(\overline{\mathbb{R}_{+}^{n}}\right)\) 满足 \(\operatorname{spt}\left(\tilde{v}_{i k}\right) \subset B_{1}(O),\left\|\tilde{v}_{i k}-\tilde{v}_{i}\right\|_{m, p, B_{1}^{+}(O)}=\left\|\tilde{v}_{i k}-\tilde{v}_{i}\right\|_{m, p, \mathbb{R}_{+}^{n} \rightarrow 0}(k \rightarrow \infty)\). 回到变量 \(\boldsymbol{x}\), 由 6 式知存在 \(u_{i k} \in C^{m}\left(\overline{O_{i} \cap \Omega}\right)\) 满足
(4): 令
\[\tilde{u}_{i k}=\left\{\begin{array}{ll} u_{i k}, & x \in O_{i}, \\ 0, & x \in \Omega \backslash O_{i}, \end{array} \quad u_{k}=\sum_{i=0}^{N} \tilde{u}_{i k} .\right. \]显然 \(u_{k} \in C^{m}(\bar{\Omega})\), 并且
\[\operatorname{spt}\left(u_{i k}\right) \subset O_{i}, \quad\left\|u_{i k}-u_{i}\right\|_{m, p, O_{i} \cap \Omega} \leqslant C\left\|v_{i k}-v_{i}\right\|_{m, p, B_{1}^{+}} \rightarrow 0, \quad k \rightarrow \infty \]\[\begin{aligned} \left\|u-u_{k}\right\|_{m, p, \Omega} & =\left\|\sum_{i=0}^{N}\left(u_{i}-u_{i k}\right)\right\|_{m, p, \Omega} \leqslant \sum_{i=0}^{N}\left\|u_{i}-u_{i k}\right\|_{m, p, \Omega} \\ & =\sum_{i=0}^{N}\left\|u_{i}-u_{i k}\right\|_{m, p, \Omega \cap \Omega_{i}} \rightarrow 0 . \end{aligned} \]因此定理得证.
2.2.4 逼近定理的应用
定理 15. \(C_{0}^{\infty}\left(\mathbb{R}^{n}\right)\) 在 \(W^{k, p}\left(\mathbb{R}^{n}\right)\) 中稠.
证明: 对 \(u\) 进行磨光, 那么 \(J_{\varepsilon} u \in C^{\infty}\left(\mathbb{R}^{n}\right)\), 对固定的 \(\varepsilon\), 记 \(w=J_{\varepsilon} u\), 我们取截断函数 \(\zeta \in C_{0}^{\infty}\left(B_{2}(0)\right), 0 \leq \zeta \leq 1\), 且在 \(B_{1}(0)\) 上有 \(\zeta=1\), 令:
\[w_{k}(x)=w \zeta\left(\frac{x}{k}\right) \]因此 \(w_{k} \in C_{0}^{\infty}\left(\mathbb{R}^{n}\right)\), 利用莱布尼茨求导法则:
\[\begin{aligned} \mathrm{D}^{\boldsymbol{\alpha}} w_{k}(\boldsymbol{x}) & =\sum\left(\begin{array}{c} \boldsymbol{\alpha} \\ \boldsymbol{\beta} \end{array}\right) \mathrm{D}^{\boldsymbol{\beta}}\left(\zeta\left(\frac{\boldsymbol{x}}{k}\right)\right) \mathrm{D}^{\boldsymbol{\alpha}-\boldsymbol{\beta}} w \\ & =\zeta\left(\frac{\boldsymbol{x}}{k}\right) \mathrm{D}^{\boldsymbol{\alpha}} w+\sum_{\substack{\boldsymbol{\beta} \leqslant \boldsymbol{\alpha} \\ |\boldsymbol{\beta}|>0}}\left(\begin{array}{c} \boldsymbol{\alpha} \\ \boldsymbol{\beta} \end{array}\right) k^{-|\boldsymbol{\beta}|}\left(\mathrm{D}^{\boldsymbol{\beta}} \zeta\right)\left(\frac{\boldsymbol{x}}{k}\right) \mathrm{D}^{\boldsymbol{\alpha}-\boldsymbol{\beta}} w \end{aligned} \]因此:
\[\begin{aligned} \left\|D^{\alpha} w_{k}-D^{\alpha} w\right\| & \leq\left\|\zeta\left(\frac{x}{k}\right) D^{\alpha} w-D^{\alpha} w\right\|_{p}+\left|\sum_{\substack{\boldsymbol{\beta} \leqslant \boldsymbol{\alpha} \\ |\boldsymbol{\beta}|>0}}\left(\begin{array}{c} \boldsymbol{\alpha} \\ \boldsymbol{\beta} \end{array}\right) \frac{1}{k^{|\boldsymbol{\beta}|}}\left(\mathrm{D}^{\boldsymbol{\beta} \zeta}\left(\frac{\boldsymbol{x}}{k}\right)\right) D^{\boldsymbol{\alpha}-\boldsymbol{\beta}} w\right|_{0, p, \mathbb{R}^{n}} \\ & \leq\left(\int_{|\boldsymbol{x}|>k}\left|\mathrm{D}^{\boldsymbol{\alpha}} w\right|^{p} d \boldsymbol{x}\right)^{\frac{1}{p}}+\frac{C}{k}\|w\|_{m, p, \mathbb{R}^{n} \rightarrow 0, \quad k \rightarrow \infty} \end{aligned} \]取 \(u_{k}=w_{k}\) 命题即得证明.
例 16. (求导法则) 若 \(\phi_{1}, \frac{\partial \phi_{1}}{\partial x_{i}} \in L^{p}(\Omega), \phi_{2}, \frac{\partial \phi_{2}}{\partial x_{i}} \in L^{p^{\prime}}(\Omega), \frac{1}{p}+\frac{1}{p^{\prime}}=1\), 则 \(\phi_{1} \phi_{2} \in L^{1}(\Omega)\) 且
\[\frac{\partial}{\partial x_{i}}\left(\phi_{1} \phi_{2}\right)=\phi_{1} \frac{\partial \phi_{2}}{\partial x_{i}}+\phi_{2} \frac{\partial \phi_{1}}{\partial x_{i}} \]\[\int\left(\phi_{1} \phi_{2}\right) \frac{\partial \phi}{\partial x_{i}} \mathrm{dx}=-\int\left(\phi_{1} \frac{\partial \phi_{2}}{\partial x_{i}}+\phi_{2} \frac{\partial \phi_{1}}{\partial x_{i}}\right) \phi \mathrm{d} \boldsymbol{x} \]特别地, 当 \(\phi_{1}, \phi_{2} \in H^{1}(\Omega)\) 时, 结论成立.
证明:等价于证明:对于任意的 \(\phi \in C_{0}^{\infty}(\Omega)\), 都有:
我们对 \(\phi_{i}\) 进行磨光, 得到了 \(J_{\varepsilon} \phi_{i}\), 由Holder不等式可知:
因此 \(\phi_{1} \cdot \phi_{2} \in L^{1}\). 由于磨光后的函数是满足对应的分部积分的,因此:
\[\int_{\Omega} J_{\varepsilon} \phi_{1} J_{\varepsilon} \phi_{2} \frac{\partial \phi}{\partial x_{i}} d \boldsymbol{x}=-\int_{\Omega}\left(J_{\varepsilon} \phi_{1} \frac{\partial\left(J_{\varepsilon} \phi_{2}\right)}{\partial x_{i}}+\frac{\partial}{\partial x_{i}}\left(J_{\varepsilon} \phi_{1}\right) \cdot J_{\varepsilon} \phi_{2}\right) \phi \mathrm{d} \boldsymbol{x}, \]现在我们只需要证明等式中的对\(\varepsilon\)取极限结论是成立的即可.
\[\begin{aligned} & \left|\int_{\Omega} J_{\varepsilon} \phi_{1} \cdot J_{\varepsilon} \phi_{2} \frac{\partial \phi}{\partial x_{i}} d \boldsymbol{x}-\int_{\Omega} \phi_{1} \phi_{2} \frac{\partial \phi}{\partial x_{i}} d \boldsymbol{x}\right| \\ \leqslant & \int_{\Omega}\left|J_{\varepsilon} \phi_{1}-\phi_{1}\right| J_{\varepsilon} \phi_{2}|| \frac{\partial \phi}{\partial x_{i}}\left|d \boldsymbol{x}+\int_{\Omega}\right| \phi_{1}\left|J_{\varepsilon} \phi_{2}-\phi_{2}\right|\left|\frac{\partial \phi}{\partial x_{i}}\right| \mathrm{d} \boldsymbol{x} \\ \leqslant & M\left|J_{\varepsilon} \phi_{1}-\phi_{1}\right| L^{p}\left|J_{\varepsilon} \phi_{2}\right|_{L^{p^{\prime}}}+\left|\phi_{1}\right|_{L^{p}}\left|J_{\varepsilon} \phi_{2}-\phi_{2}\right|_{L^{p^{\prime}}} \cdot \sup _{x \in \Omega}\left|\frac{\partial \phi}{\partial x_{i}}\right| \rightarrow 0, \quad \varepsilon \rightarrow 0 . \end{aligned} \]同理可证右侧.
例 17. 设 \(1 \leqslant p<\infty\), 又设 \(u, v \in W^{1, p}(\Omega) \cap L^{\infty}(\Omega)\), 则 \(u v \in W^{1, p}(\Omega) \cap L^{\infty}(\Omega)\) 且
\[\frac{\partial}{\partial x_{i}}(u v)=\frac{\partial u}{\partial x_{i}} v+u \frac{\partial v}{\partial x_{i}}, \quad x \in \Omega, i=1, \cdots, n \]证明思想和上边的求导法则 \(r\) 如出一辙.
例 18. (复和运算) 设 \(\Omega \subset \mathbb{R}^{n}\) 是有界开集. 若 \(f(y) \in C^{1}\left(\mathbb{R}^{1}\right),\left|f^{\prime}(y)\right| \leqslant M, y \in u \in W^{1, p}(\Omega)\), 则 \(g(\boldsymbol{x})=f(u(\boldsymbol{x})) \in W^{1, p}(\Omega)\) 且有链式法则
\[\frac{\partial g(\boldsymbol{x})}{\partial x_{i}}=\frac{\partial}{\partial x_{i}} f(u(\boldsymbol{x}))=f^{\prime}(u(\boldsymbol{x})) \frac{\partial u}{\partial x_{i}}, \quad i=1,2, \cdots, n \]且如果 \(u \in W^{1, p}\), 那么 \(u^{+}, u^{-},|u| \in W^{1, p}\). 且
\[D u^{+}(x)=\left\{\begin{array}{cc} D u(x), & u(x)>0 \\ 0, & u(x) \leq 0 \end{array}, D u^{-}(x)=\left\{\begin{array}{cc} D u(x), & u(x)<0 \\ 0, & u(x) \geqslant 0 \end{array}\right.\right. \]证明: 由逼近定理可知存在 \(u_{k} \in C^{1} \cap W^{1, p}\) 使得:
\[\left\|u_{k}-u\right\|_{1, p} \rightarrow 0 \]注意到:
\[\int\left|f\left(u_{k}\right)-f(u)\right| \mathrm{dx} \leqslant \int M\left|u_{k}-u\right| \mathrm{dx} \rightarrow 0 \]以及:
\[\begin{aligned} & \int_{\Omega}\left|f^{\prime}\left(u_{k}\right) \frac{\partial u_{k}}{\partial x_{i}}-f^{\prime}(u) \frac{\partial u}{\partial x_{i}}\right| \mathrm{d} \boldsymbol{x} \\ \leqslant & M \int_{\Omega}\left|\frac{\partial u_{k}}{\partial x_{i}}-\frac{\partial u}{\partial x_{i}}\right| \mathrm{d} \boldsymbol{x}+\int_{\Omega}\left|f^{\prime}\left(u_{k}\right)-f^{\prime}(u)\right|\left|\frac{\partial u}{\partial x_{i}}\right| \mathrm{d} x \end{aligned} \]第一项是自然的趋于 0 的,第二项可以被 \(2 M|\mathrm{Du}|\) 控制, 因此利用 Lebesgue控制收敛定理也可以得知当 \(k \rightarrow \infty\) 时,其极限为 0
由于 \(f, u_{k}\) 是光滑的, 因此求导法则成立, 故有:
\[\int_{\Omega} f\left(u_{k}(x)\right) \frac{\partial \phi}{\partial x_{i}} d \boldsymbol{x}=-\int_{\Omega} \frac{\partial f\left(u_{k}\right)}{\partial x_{i}} \phi \mathrm{d} \boldsymbol{x}=-\int_{\Omega} f^{\prime}\left(u_{k}\right) \frac{\partial u_{k}}{\partial x_{i}} \phi \mathrm{d} \boldsymbol{x} . \]利用前边建立的两个不等式就可以得到证明.
以 \(u^{+}\)为例. 我们取特别的逼近函数:
\[f_{\varepsilon}(t)= \begin{cases}\left(t^{2}+\varepsilon^{2}\right)^{1 / 2}-\varepsilon, & t>0 \\ 0 & , t \leqslant 0\end{cases} \]将 \(f_{\varepsilon}\) 带入 \(f\), 令 \(\varepsilon \rightarrow 0\), 于是定理得证.
标签:Sobolev,partial,boldsymbol,right,空间,frac,Omega,left From: https://www.cnblogs.com/mathzhou/p/17620084.html