线性代数
前言:
最近咕咕咕了好久了,1是因为换了教室,2是因为很多题在做,没时间,3则是因为上了线性代数。
矩阵
在c++中,矩阵可以用二维数组来表示,但是乘法的运算有点不同,要重新定义
矩阵的基本运算
1.加/减/数乘运算:直接一一对应直接运算即可
2.乘法运算:遵循左行右列原则,一一对应相乘在相加得到答案
举个例子,c=ab的话,c_i,j=sum(k) a_i,k * b_k,j
注意点:不具有交换律,但具有结合律,时间在O(n^3)
小技巧:ij的矩阵和jm的矩阵乘法后得到im的矩阵,所以利用结合律先算小矩阵
时间复杂度将会大幅度降低!
3.转置,A的转置A^T=所有的swap(A_i,j,A_j,i)
4.求逆,B是A的逆当且仅当A*B=I。(矩阵乘法意义下)
5.矩阵快速幂(即重新定义乘法后的快速幂)
特殊矩阵
1.单位矩阵I,满足I的主对角线为1,其余都是0,具有A*I=A的性质,可以手推
2.三角矩阵,也分为上三角和下三角两种:
前者:主对角线为分界线(不包括),左下角都是0。
后者:主对角线为分界线(不包括),右上角全是0。
OI中主要常出现这两种,其他不再赘述
矩阵运算的应用
矩阵加速dp
前提:矩阵快速幂
模板链接:https://www.luogu.com.cn/problem/P3390
I have a 矩阵乘法。
I have a 快速幂。
ah~~矩阵快速幂。
个人建议看题解,像题解那样写结构体,更好做。
ac代码:https://www.luogu.com.cn/record/118986645
注:我最开始没听老师劝告,非要自己写,然后后面改回标程做法历程有点烦人,所以看好题解啊!
加速线性dp
这个举个例子,斐波那契,要你求114514114514项,就算记忆化也没p用了。
考虑矩阵的做法:
如图,发现这个矩阵全是常数没有变量,那就成功了!

为什么这么做呢,因为我这样就可以表示成f1*矩阵的某某次方了,快速幂搞定!
例题1:https://www.luogu.com.cn/problem/P3216
思路:这道题矩阵推理出来发现总是和n长度脱不了干系,但他只有1e18啊,所以大不了
我做18种矩阵,分段乘除即可。
ac代码:https://www.luogu.com.cn/record/118988258
例题2:Arc of dream
思路:推理很麻烦,要尽量把乘除拆开变为加减,最后形成了很多项,推的有点小麻烦。
注:vjudge上直接找吧(这现在用的电脑网速太慢)。
广义矩阵运算
这个要详细总结一下
先给题目来看:
https://www.luogu.com.cn/problem/P6190
分析:
F(i,j,k)表示从i到j使用k次魔法的最短路。
F(i,j,0)就是Floyd。
F(i,j,1)=min_{u,v} F(i,u,0)+F(v,j,0)-w(u,v) 。
F(i,j,k)=min_u F(i,u,k-1)+F(u,j,1) k>2。
可以发现,在一次的基础上,就可以矩阵快速幂了。
你问:这个和矩阵乘法有√8关系啊。
要是我把求和符号改成min,把乘积改为求和,那不就是啦!这时候就是广义矩阵运算了!
矩阵应用的一些总结(主要是思路上)
1.以统计方案数为例,假设当前状态可以由n个点转移过来,并且转移过来的方案数都是1。
那么可以让这个是常数矩阵变为01矩阵,可以转移的为1,否则为0,那么乘上矩阵k次幂就是k次转移的ans。
其实这个0/1矩阵可以看成一种邻接表。
例题:
Quad Tiling(poj) 这一题实际上只有可能6种状态,能到达状态间为1(注意不是双向)
魔法值(https://www.luogu.com.cn/problem/P6569)
2.当你dp柿子写出来了,但是又有困惑,不如尝试矩阵来简化。
注:矩阵也可以用在线段树上哦,每个rt都创建一个矩阵,修改也是修改某个矩阵即可。
例题:Can you answer these queries III(https://www.luogu.com.cn/problem/SP1716)
3.要看出广义矩阵乘法还是很难滴,关键要了解清楚矩阵乘法的原理和写法,然后发散思维。
太难了,怎么发散嘛~~~
这里有常见的模型:
a.加法改乘法,乘法改为异或。
b.加法改为min/max,乘法改为加减。
高斯消元(矩阵基础上)
你可曾结果n元一次方程组?
恭喜你,你已经会一半高斯消元了!
在程序中,对方程的操作常常是:
a.交换两个方程的顺序
b.把一个方程的若干倍加到另外一个方程上
c.把一个方程同时乘或者除若干倍
那么和矩阵有什么关系呢?
首先让我们用矩阵乘法来表示很多很多方程组:如图中(1)
然后呢,很显然操作a就是交换矩阵两行,b,c操作同理也可以用矩阵完成
那么,我们对最终矩阵的期望是什么呢?希望他长成什么b样?
我们当然是期望一个I矩阵啦,那么这样一个元素对应一个答案,多好啊
但是期望有时候并不能成真,因为可能存在无解或者是x_n有无限解的情况呢......
甚至,可能方程数量和未知数的个数都不是相等的,这样君又该如何应对?
这里请上两种矩阵,一种我建议在实数域中使用,另一种在整数域中使用
图例子:
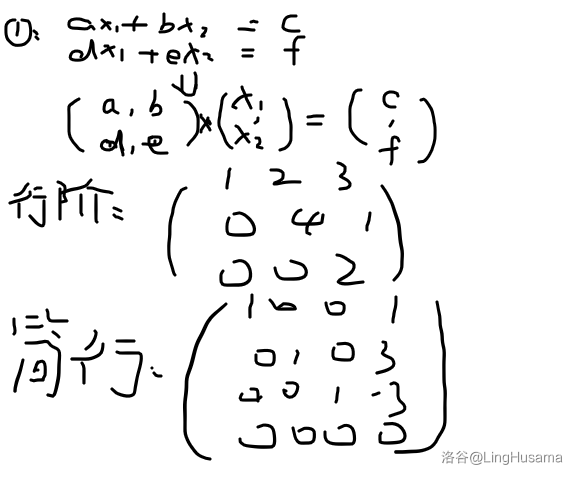
整数域使用(当然也可以实数域):行阶梯式矩阵
矩阵要求:
1.所有非全零行要在全零行之上
2.每一行第一个非零数的位置要严格位于上一行第一个非零数的右侧
达成矩阵的方法:
找主元(这一排之后中找)(可以任意了),换主元(非0),这一列消除这一排下面的非0数为0。
这里因为是整数域,所以用辗转相除法
对应算法:高斯消元。
假设我们已经得到了行阶梯式矩阵
先判断无解:如果一个全部为0的行,其对应的答案不为0,无解
其次判断某些元素是否存在无数解情况:(我个人想的)
我们从最后一行向上找,统计能够统计的x的答案并统计x是否有无限解(如果有,x的答案命令为0)
注:不知道是否有无限:-1,一定无限:1,一定不无限:0,一开始全部为-1,令其为f
假设我们现在统计到h行了
首先我们找到这一行第一个非0的位置,假设其所在的位置为p
由于行阶梯式,其下面的肯定比他“短”所以所有p后面的元素应该都是遍历过的
这时候可能出现后面有f=-1的情况,那么肯定是无限解了,令f=1
然后我们知道,只要对于这个方程x_p后面的x_p+1到x_p+n而言,如果有一个解是无限的,
那么p这里肯定也是无限的(会随之变化),这样就命令其f为1
反之后面全为确定的值,相应x_p也确定的,带入计算x_p并令f为0即可。
代码:
#include<bits/stdc++.h>
using namespace std;
int a[4005][4005];
int ans[4005];
int notd[4005];
int n,m;
void swp(int st,int x,int y){
for(int i=st;i<=m+1;i++){
swap(a[x][i],a[y][i]);
}
}
void sub(int st,int x,int y){
int tmp=a[x][st]/a[y][st];
for(int i=st;i<=m+1;i++){
a[x][i]-=tmp*a[y][i];
}
}
int main(){
scanf("%d%d",&n,&m);
memset(ans,0,sizeof(ans));
memset(notd,-1,sizeof(notd));
for(int i=1;i<=n;i++){
for(int j=1;j<=m+1;j++){
scanf("%d",&a[i][j]);
}
}
int c=1;//枚举开始的位置 ,因为可能存在一列都为0的情况,但此时又不能跳行,应该是c
for(int i=1;i<=m;i++){//现在正在处理的列
int now=c;
for(int j=c+1;j<=n;j++){
if(a[c][i]<0){
for(int kk=i;kk<=m+1;kk++){
a[c][kk]*=-1;
}
}
if(a[j][i]<0){
for(int kk=i;kk<=m+1;kk++){
a[j][kk]*=-1;
}
}
//首项系数化为正
if(a[c][i]<a[j][i]){//把大的换到这一行来去 ,这里再放一次是为了保证0的RE问题
swp(i,c,j);
}
while(a[j][i]){
if(a[c][i]<a[j][i]){//把大的换到这一行来去
swp(i,c,j);
}
sub(i,c,j);
swp(i,c,j);
}
}
if(a[c][i]==0){
continue;
}
c++;
}
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m+1;j++){
// printf("%d ",a[i][j]);
// }
// printf("\n");
// }
//这就是普通的高斯消元了,开始回代检验
for(int i=1;i<=n;i++){//判断无解
int have=0;
for(int j=1;j<=m;j++){
if(a[i][j]!=0){
have++;
}
}
if(have==0&&a[i][m+1]!=0){
printf("No solution");
return 0;
}
}
for(int i=n;i>=1;i--){//回代检验,最后一行开始
int an=a[i][m+1];
int have=0;
int pos=0;
bool pan=0;
for(int j=1;j<=m;j++){
if(a[i][j]!=0&&pos==0){
pos=j;
have++;//寻找主元位置
}
}
if(pos==0){
continue;
}
for(int j=pos+1;j<=m;j++){
if(notd[j]==-1){
notd[j]=1;//到了这一项,后面还不确定的都是无限的 (1)
}
}
for(int j=pos+1;j<=m;j++){
if(a[i][j]!=0){
have++;
if(notd[j]==1){//后面组合体中,有一个无限,则整体无限(1)
notd[pos]=1;
break;
}
}
}
if(notd[pos]==1){
ans[pos]=0;//不会影响后面的,因为唯一值的答案不会涉及到他,很多答案的则是看到notd就输出
continue;
}
if(have==1){
ans[pos]=an/a[i][pos];
notd[pos]=0;//肯定能确定的
}
else{
for(int j=pos+1;j<=m;j++){
an-=ans[j]*a[i][j];
}
ans[pos]=(an/a[i][pos]);
if(notd[pos]==-1){//如果后面全是确定的,那么这个肯定是确定的(0)
notd[pos]=0;
}
}
}
for(int i=1;i<=m;i++){
printf("X[%d] ",i);
if(notd[i]==1){
printf("not determined\n");//无限解的情况
}
else{
printf("= %d\n",ans[i]);
}
}
}
实数域使用(整数域用lcm会容易导致爆long long):简化行阶梯
矩阵要求:
1.它是个行阶梯矩阵。
2.每一行第一个非零数必须为1,且在这一列中除了他为1外其余都是0
显然这个应该是高斯消元的高级版,但缺陷可能比高斯多
算法:高斯-若当消元
算法晋升:对于某一行,找主元找abs最大的,
并且要求主元确定后每一行都找和消而不是从下一行开始找和消
算法垃圾处:无法应用辗转相除,只能利用lcm,然后爆long long......
判断无解:同上
判断多解:这一行只有1个1时,这个1对应的就是唯一解,否则都是无限解
代码:
#include<bits/stdc++.h>
using namespace std;
double a[405][405];
double eps=1e-8;
bool ans[405];
int main(){
int n,m;
scanf("%d%d",&n,&m);
memset(ans,0,sizeof(ans));
for(int i=1;i<=n;i++){
for(int j=1;j<=m+1;j++){
scanf("%lf",&a[i][j]);
a[i][j]=1.0000*a[i][j];
}
}
int c=1;//枚举开始的位置 ,因为可能存在一列都为0的情况,但此时又不能跳行,应该是c
for(int i=1;i<=m;i++){//现在正在处理的列
int now=c;
for(int j=c+1;j<=n;j++){//寻找绝对值最大的
if(fabs(a[j][i])-fabs(a[now][i])>eps){
now=j;
}
}
for(int j=i;j<=m+1;j++){
swap(a[now][j],a[c][j]);//交换过去
}
if(a[c][i]==0)//最大值等于0则说明该列都为0,肯定无解
{
continue;
}
for(int j=i+1;j<=m+1;j++){
a[c][j]=1.0*a[c][j]/a[c][i];//首项系数化为1
}
a[c][i]=1;
for(int j=1;j<=n;j++){//开始消除
if(j==c){
continue;
}
double tmp=1.0000*a[j][i];//目标对象缩放系数
for(int k=i;k<=m+1;k++){
a[j][k]-=1.0000*tmp*a[c][k];
}
}
c++;
}
for(int i=1;i<=n;i++){
// for(int j=1;j<=m+1;j++){
// printf("%.4lf ",a[i][j]);
// }
// printf("\n");
bool pan=1;
for(int j=1;j<=m;j++){
if(fabs(a[i][j])>eps){
pan=0;
break;
}
}
if(fabs(a[i][m+1])>eps&&pan==1){
printf("No solution");
return 0;
}
}
for(int i=1;i<=n;i++){
int have=0;
for(int j=1;j<=m;j++){
if(fabs(a[i][j])>eps){
have++;
}
}
if(have==1){
for(int j=1;j<=m;j++){
if(fabs(a[i][j])>eps){
ans[j]=1;
break;
}
}
}
}
for(int i=1;i<=m;i++){
printf("X[%d] ",i);
if(ans[i]==1){
int to;
for(int j=1;j<=n;j++){
if(fabs(a[j][i])==1){
to=j;
}
}
if(abs(a[to][m+1])<eps){
a[to][m+1]=0;
}
printf("= %.4lf\n",a[to][m+1]);
}
else{
printf("not determined\n");
}
}
}
高斯消元拓展:
个人感觉,其实只要能看出是很多方程组就好了。
1.异或高斯消元
例题1:开关问题(oj上搜吧)http://222.180.160.110:1024/contest/4036/problem/3
ac代码:不好贴过来
例题2:和谐矩阵:https://www.luogu.com.cn/problem/P3164
ac代码:https://www.luogu.com.cn/record/119012132
2.离线给出常数的高斯消元
对于离线给出常数,例如分别为b1,b2,b3....bn,直接把他们接在原来矩阵后跟着算不就完了,不会互相影响
例题:虫食算 https://www.luogu.com.cn/problem/P1092
ac代码:https://www.luogu.com.cn/record/119012885