直接容斥。
总方案 - 一题出现四次 - 一题出现三次 - 一题出现两次。
一题出现两次的情况略有不同,注意考虑周全。
复杂度 \(O(n)\)。
有技巧的博弈论。
如果当前点的所有出边均为先手必胜,那么当前点为先手必败。
否则先手必胜。
于是我们可以建一个反向图,初始状态都设为 \(0\),跑拓扑排序即可。
为什么不用记忆化呢?因为环的情况不好处理,而且卡时间。
复杂度 \(O(q(n+m))\)。
简单构造题。
假设有一个包含 \(n\) 个节点的简单环,那么符合要求的点对为 \(\frac{n(n-1)}{2}\)。
所以我们考虑构造出一些环,相邻的环连一条边,容易证明一定能凑出 \(k\)。
复杂度 \(O(1)\)。
简单树形 DP。
对于当前点 \(u\),找到其所有儿子 \(v\) 中最大和次大的链,拼在一起。
注意当前点为根和只有一个儿子的情况。
复杂度 \(O(n)\)。
每次找到距离最近的一对圆,加上他们相交的时间并删除。
反复操作直到没有圆。
复杂度 \(O(n^3)\)。
大模拟。
枚举罪犯和日期,判断有多少人说谎。
复杂度 \(O(mp)\)。
F1:树上差分。
把路径上的边 \(+1\),覆盖 \(0\) 次、\(1\) 次、多次的情况分别讨论。
复杂度 \(O(n\log n)\)。
F2:类似 DP。
考虑每一条边覆盖几次,实际上只有三种情况。
所以对于当前节点 \(u\),我们考虑有几条路径跨越了 \(u\) 到 \(fa\) 的边。
仔细一想,我们发现可以从子树转移。
首先我们将树分为三个部分。
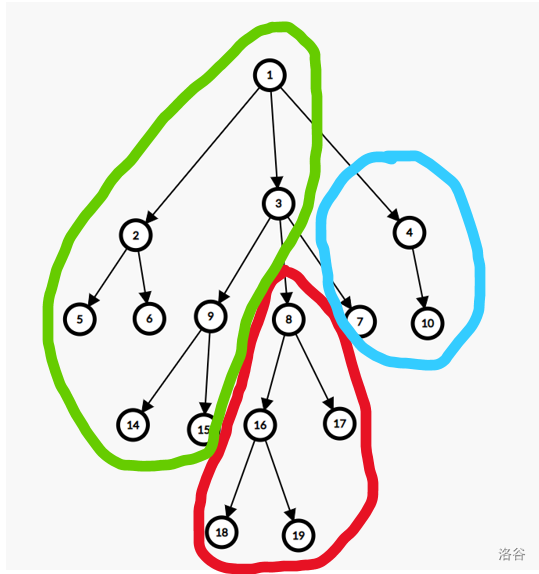
每个点维护起点在红色区域,终点在绿色区域且 dfs 序最小和次小的路径。
再维护起点在红色区域,终点在蓝色区域且 dfs 序最大和次大的路径。
这样就可以由子树传递上来,然后处理一下只保留四条特殊路径即可。
复杂度 \(O(n)\)。
二分答案。
check 的时候用队列记录评测任务,然后从左到右贪心地评测即可。
如果超过时间 \(D\),或者最后队列不为空,返回 false。
复杂度 \(O(n\log n)\)。
F1:决策单调性+分治优化 DP。
首先可以断环为链。
枚举起点 \(l\),定义 \(f_{i,j}\) 表示在 \([l,i]\) 中开 \(j\) 扇门的最小代价。
然后就有了单次操作 \(O(n^2m)\) 的 DP,即:
\[f_{i,j}=\min_{k=l}^{i}(f_{k-1,j-1}+sum_{k,i}) \]其中 \(sum_{i,j}=\sum\limits_{t=i}^{j}a_t\cdot (t-i)\),可以预处理。
观察发现,如果 \(f_{i,j}\) 的最后一扇门在 \(w\),那么对于所有 \(k<j\),\(f_{k,j}\) 的最后一扇门在 \(w\) 左侧,反之同理。
于是可以枚举 \(l\) 和 \(j\),对于 \(f_{l,j}\) 到 \(f_{l+n-1,j}\) 分治处理。
具体可以定义 \(dfs(x,l,r,L,R)\) 表示当前有 \(x\) 扇门,\(f\) 第一维范围为 \([l,r]\),决策范围为 \([L,R]\)。每次计算出 \(mid=\frac{l+r}{2}\),暴力算出 \(f_{mid,x}\) 的最优决策点 \(w\),然后递归 \(dfs(x,l,mid-1,L,w)\) 和 \(dfs(x,mid+1,r,w,R)\)。
复杂度 \(O(mn^2\log n)\)。
F2:斜率优化DP。
待更。
容易想到一条路径的两个端点必定为这棵无根树的叶子节点。
我们考虑 “剥洋葱”,每次找到最外层的叶子节点,答案加上 \(\min(cnt,2\cdot m)\),其中 \(cnt\) 为叶子节点的个数。
然后拓扑排序去掉最外层,直到把整棵树都去除。
至于证明,仔细想想就明白了。
复杂度 \(O(n)\)。
考虑 \(40pts\) 的暴力。
以 \(x\) 为关键字从小到大排序,对于当前节点 \(u\),找到前面所有纵坐标小于 \(u\) 的纵坐标的点集的最长下降序列,直接从后往前找即可。
考虑分治优化。
假设当前区间为 \([l,r]\),计算出 \(mid=\frac{l+r}{2}\),递归处理 \([l,mid]\) 和 \([mid+1,r]\)。
然后将 \([l,r]\) 以纵坐标为关键字从小到大排序。
左边维护一个数组 \(vec_1\) 记录下降序列,右边维护一个数组 \(vec_2\) 记录上升序列。(本质上就是单调栈)
找到 \(vec_2\) 中倒数第二个元素的纵坐标 \(y\),并在 \(vec_1\) 中二分,找到有多少个点的纵坐标大于 \(y\) 即可。
复杂度 \(O(n\log^2n)\)。
标签:code,NOI,题解,复杂度,mid,春季,dfs,纵坐标,DP From: https://www.cnblogs.com/HQJ2007/p/17561605.html