概念
我们考虑这样一个问题:求 \(\sum_{i=1}^{k} \lfloor \dfrac{n}{i} \rfloor\)
我们以 \(n=7,k=7\) 为例子,先画出 \(f(x) = \dfrac{7}{x} \ (1 \leq x \leq 7)\) 的图像
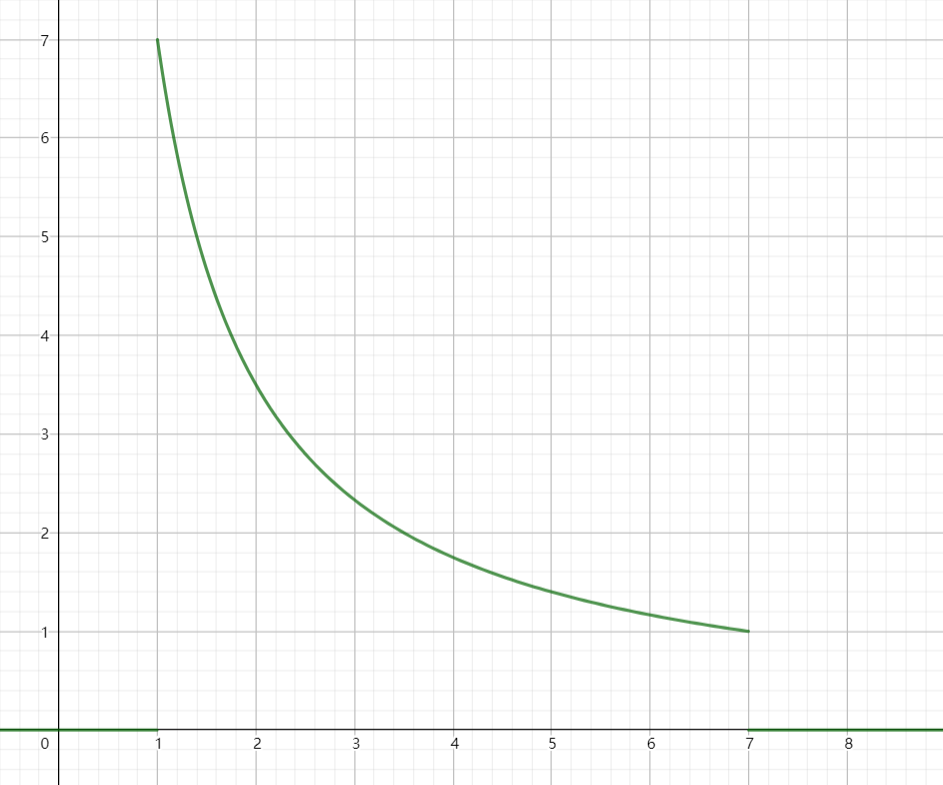
因为我们的取值是向下取整的,我们描出所有可能的取值
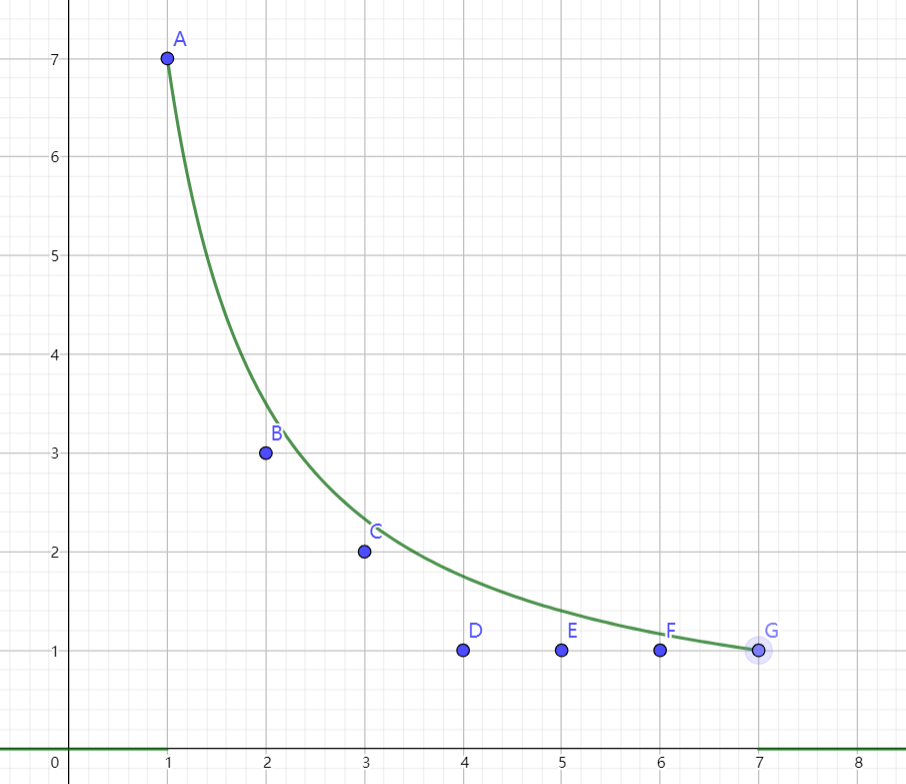
注意到所有的点按照取值可以分成若干段
我们可以一次性处理一个段的答案,把整段对答案的贡献加上即可
这就是数论分块
实现
如果要实现整块一起统计,我们需要求出每一块的块头 \(l\) 和块尾 \(r\),则:
\[Ans = \sum_{i=1}^{k} \lfloor \dfrac{n}{i} \rfloor = \sum_{[l,r]} (r-l+1)(\lfloor \dfrac{n}{l} \rfloor) \]注意到每一块的 \(l\) 都可以由上一块的 \(r\) 推出,故我们继续讨论如何在已知 \(l\) 的情况下推出 \(r\)
令 \(t = \lfloor \dfrac{n}{l} \rfloor\) ,容易得到
\[\begin{cases} r = \min(\lfloor \dfrac{n}{t} \rfloor,n) \ \ \ &(t \neq 0) \\ r = n \ \ \ &(t=0) \end{cases} \]直接计算即可
应用
P2261 [CQOI2007]余数求和
先推式子
\[\begin{aligned} G(n,k) &= \sum_{i=1}^{n} k \bmod i \\ &= \sum_{i=1}^{n} k - i \times \lfloor \dfrac{k}{i} \rfloor \\ &= nk - \sum_{i=1}^{n} i \times \lfloor \dfrac{k}{i} \rfloor \end{aligned} \]直接用数论分块解决即可
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
ll n, k, res;
signed main() {
scanf("%lld%lld", &n, &k);
for (ll l = 1, r; l <= n; l = r + 1) {
r = (k / l) ? min(k / (k / l), n) : n;
res += (k / l) * ((l + r) * (r - l + 1) >> 1);
}
printf("%lld", n * k -res);
return 0;
}
P3935 Calculating
令 \(g(x) = \sum_{i=1}^{n} f(i)\) ,则
\[\sum_{i=l}^{r} = g(r) - g(l-1) \]我们推一下 \(g(x)\)
\[\begin{aligned} g(x) &= \sum_{i=1}^{x} f(i) \\ &= \sum_{i=1}^{x} \sum_{j=1}^{x} [i \mid j] \\ &= \sum_{i=1}^{x} \lfloor \dfrac{x}{i} \rfloor \end{aligned} \]直接用数论分块解决即可
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const ll Mod=998244353;
ll l, r;
inline ll g(ll n) {
ll res = 0;
for (ll l = 1, r; l <= n; l = r + 1) {
r = (n / l) ? min(n / (n / l), n) : n;
res = (res + (n / l) * (r - l + 1)) % Mod;
}
return res;
}
signed main() {
scanf("%lld%lld", &l, &r);
printf("%lld", ((g(r) - g(l - 1)) % Mod + Mod) % Mod);
return 0;
}