做着做着 cdq 分治的题发现自己太菜了写不出来题 XD,所以来写写学习笔记。
CDQ 分治
CDQ 分治一般有两个用途:解决偏序问题、将动态问题转化为静态问题。
偏序问题
我们先来介绍第一个问题:偏序问题。
普通的二维偏序就类似于逆序对,每个元素有两个属性 \(a_i, b_i\),我们需要统计 \(a_i<a_j, b_i<b_j\) 的数对 \((i, j)\) 的数量。我们可以通过归并排序或者是树状数组来计算,时间复杂度 \(O(n\log n)\)。
而对于三维偏序,即统计 \(a_i<a_j, b_i<b_j, c_i<c_j\) 的数量,我们就可以使用 cdq 分治来解决。
具体的算法流程为:
把 \([l, r]\) 分成两半,将两半区间递归下去处理,它们内部的偏序对自己处理,当前这一层只考虑左半边对右半边的贡献。我们按照 \(a_i\) 排好序,来消去第一维,这时,我们发现,左半边的所有数的 \(a_i\) 都小于右半边,这意味着在第一维上,我们从左半边向右半边的转移的限制消失了,这就允许我们在左右两部分进行一些乱搞操作,比如排序。
我们再把左右两边分别按照 \(b\) 排序,我们可以用一个双指针,卡住左半边中 \(b\) 小于当前的数的数(这里有点绕口 XD),用图来讲就是这样:
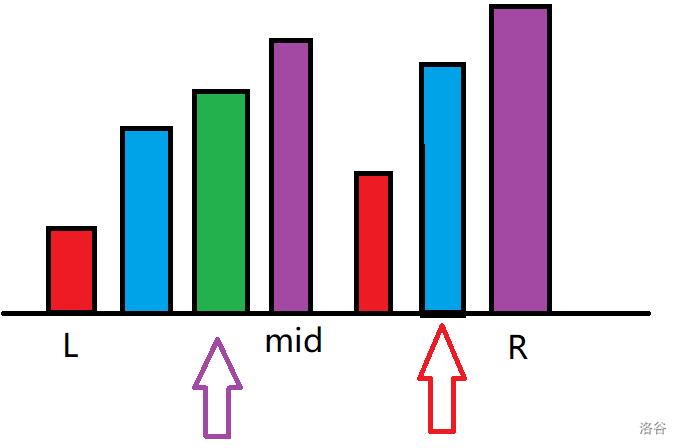
我们这时会发现现在 \(b\) 的限制也消失了,我们就只有 \(c\) 的限制了。这时我们可以直接上数据结构维护。我们把左边区间小于当前 \(b\) 的点的 \(c\) 加入到树状数组中,在查询时,我们只需要查询小于等于当前 \(c\) 的元素个数即可。
这个流程十分像归并排序,只是多了一个树状数组而已。因此时间复杂度为 \(T(n)=2T(\frac{n}{2})+O(n\log n)\),即 \(O(n\log^2 n)\)。
cdq 分治的这个用处很多,可以用来解决许多二维数点问题,并且时间复杂度也比 KD-Tree 的 \(O(n\sqrt n)\) 要好。我们可以来看几道例题:
[CQOI2011] 动态逆序对
给出 \(1\sim n\) 的排列,按照给定顺序依次删除 \(m\) 个元素,在每次删除前统计逆序对个数。
数据范围:\(1\le n \le 10^5\)。
我们把每个数看成有 \(3\) 个属性的元素,三个属性分别为 \(pos, val, time\),即它在数组中的位置,它的值,它被删除的时间。我们可以发现,它能够和别的数形成逆序对的条件为:\(pos_i < pos_j, val_i > val_j, time_i < time_j\) 或 \(pos_i > pos_j, val_i < val_j, time_i < time_j\)。这样我们就把问题转化为了一个三维偏序问题。
[SHOI2007] 园丁的烦恼
有 \(n\) 个点 \((x_i, y_i)\),\(m\) 次询问询问一个矩形区域内点的个数。
数据范围:\(n,m\le 5\times 10^5, x_i, y_i\le 10^7\)。
本题虽然和 cdq 分治无太大联系,但是我们可以把它看作一道前置题目。
我们可以先把一个询问拆成四个询问,将所有点和询问放到一起按照 \(x\) 排序,这时我们直接扫描线一下,从左向右扫,遇到一个点就加入,遇到询问则记录答案。这样就做完了,时间复杂度 \(O(n\log n)\)(KD-Tree还被卡了 www)。
而对于带插入点的问题,我们可以留到下面再看。
[SDOI2011] 拦截导弹
有 \(n\) 发导弹,每发导弹有一个速度 \(v_i\) 和一个高度 \(h_i\)。设上一次拦截的导弹为 \(j\),导弹拦截系统只能拦截 \(v_i < v_j\) 且 \(h_i < h_j\) 的导弹。问最多能拦截多少导弹,以及如果所有最优方案被选择的概率相同的话,每发导弹被拦截的概率。
数据范围:\(n\le 5\times 10^4\)。
我们很容易就能写出转移方程:设 \(f_i\) 为以第 \(i\) 发导弹结尾最多能拦截多少,\(g_i\) 为以第 \(i\) 发子弹结尾拦截的最优方案数。则有
\[f_i=1+\max _{j<i}f_j(v_i<v_j,h_i<h_j) \]\[g_i=\sum \limits_{j=1}^{i-1}g_j[f_j+1=f_i] \]这个方程直接转移的复杂度为 \(O(n^2)\)。我们考虑优化它。注意到其中有 \(3\) 个偏序关系:\(j<i, v_i<v_j, h_i < h_j\)。我们考虑用 cdq 分治优化。
首先第一维已经排好序了,我们直接来看第二和第三维。我们再把第二维排个序,和三位偏序一样,用双指针卡住,并且把第三维所代表的 dp 值加入数据结构中。这时我们需要一个查询区间最大值以及最大值出现次数的数据结构,可以考虑用线段树维护。这样第一问就做完了。
我们再考虑第二问,我们可以先把所有的方案数算出来,即 \(sum=\sum \limits_{i=1}^{n}g_i[f_i+1=ans]\)。我们再考虑每个点的出现次数。我们再反着跑一遍 dp,求出反着的最长上升序列,也算出当前的 \(g\) 值,分别记为 \(f_1(i), g_1(i)\)。
我们枚举每个点,因为它左右都为最优方案,如果 \(f(i)+f_1(i)-1 \not= ans\),则它一定不可能被拦截,否则根据乘法原理,拦截它的方案数为 \(g(i)\times g_1(i)\)。
同时,我们在这题中还需要注意转移顺序的问题。我们必须先执行 \(cdq(l, mid)\),再计算左半区间对右半区间的贡献,最后再计算 \(cdq(mid + 1, r)\)。这样是为了防止在右区间转移时用不正确的 dp 值直接转移。
动态问题转为静态问题
动态问题是指在询问的过程中可能会有修改的操作,而静态问题指所有的修改都在询问前完成。用 cdq 分治,我们可以把动态问题转化为静态问题,取而代之的是时间复杂度增加一个 \(\log n\)。
我们可以把所有操作看成一个序列,我们设 \(cdq(l, r)\) 为计算 \([l, mid]\) 的修改对 \([mid + 1, r]\) 的询问的影响。我们可以直接把 \([l, mid]\) 的修改操作全部加入,然后扫描一遍右半区间的询问,更新一遍即可。
听起来十分简单,下面来看几道例题。
简单题(弱化版)
给定一个平面,支持两种操作:在 \((x, y)\) 处添加一个权值为 \(v\) 的点、查询矩形区域内的点的权值和。
数据范围:\(q\le 10^5\)。
根据上面“园丁的烦恼”那道题,我们可以如法炮制,一个询问拆成四个询问,然后前缀和即可。但是本题带上了插入点操作。我们就需要 cdq 分治来解决。
我们考虑 \([l, mid]\) 插入的点对 \([mid + 1, r]\) 的贡献,我们可以直接把这些点全部加入到平面中,然后进行一遍扫描线即可,最后将答案累加。
时间复杂度 \(O(n\log^2n)\)。
(本人在闲来无事的时候突然想到:如果一个点能对询问产生贡献,那么必须满足 \(t_i < t_j, x_i < x_j, y_i < y_j\),好像又是一个三维偏序 XD)
天使玩偶/SJY摆棋子
平面上有 \(n\) 个点,\(m\) 次操作,有两种操作:向平面内添加点、询问与 \((x_i, y_i)\) 曼哈顿距离最近的点的曼哈顿距离。
数据范围:\(n, m\le 3\times 10^5, x_i, y_i \le 10^6\)。
我们先来考虑没有添加点的操作时怎么解决。我们可以先把曼哈顿距离中的绝对值去掉,我们在这里只讨论 \(x_a>x_b, y_a > y_b\)(\(a\) 为查询的点)时的情况,剩下的情况同理。
我们的式子就变为了求 \(x_a-x_b+y_a-y_b\) 的最小值,也就是求 \(\max (x_b+y_b)\)。我们可以先把所有询问和修改按照 \(x\) 排序,然后维护线段树,扫描到修改就在 \(y_b\) 处插入值 \(x_b+y_b\)。扫描到询问就询问所有小于 \(y_a\) 的位置的最大值即可。
而这时增加了询问,我们就需要用 cdq 分治解决。我们可以先把左半区间的修改点加入到一个集合内,再把右半区间的询问也加入到这个集合,对这个集合跑一遍上面的流程更新答案即可。
这样,一个询问总共会被更新 \(\log n\) 次,所以复杂度为 \(O(n\log^2 n)\)。
镜中的昆虫
给定一个长度为 \(n\) 的序列,支持以下两种操作:查询 \([l, r]\) 有多少不同的数值,区间覆盖。
数据范围:\(n\le 10^5\)。
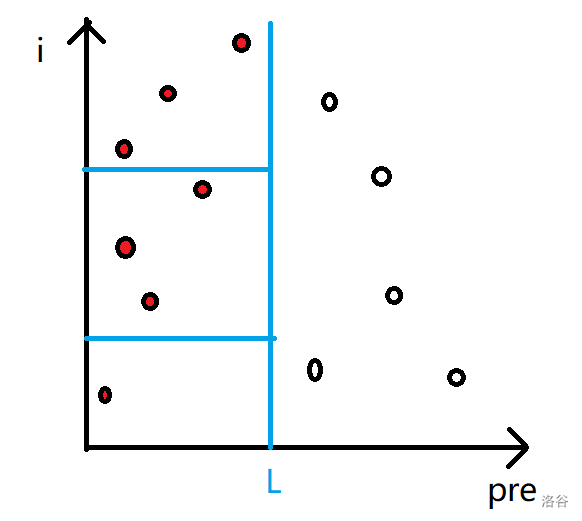
我们先考虑答案怎么统计。对于区间数颜色,有一个十分套路的方法:对每个点维护一个 \(pre_i\),即这个点往前走,第一个遇到的和它相同的颜色的点。那么这个区间的颜色数即为在这个区间内,且 \(pre_i\) 小于 \(l\) 的个数,形式化的说就是满足 \(l \le i \le r, pre_i < l\) 的个数。
是不是感觉很眼熟,这就是一个典型的二维数点。可以直接用树状数组做,像下图。
我们这样就可以统计完无修改时的答案,我们再来考虑有单点修改的情况。
我们注意到,单点修改颜色每次只会导致 \(O(1)\) 位置的 \(pre_i\) 发生变化,我们可以把这些变化也看成平面上的点,只是带上了 \(1\) 或 \(-1\) 的权值,我们用 cdq 分治直接二维数点即可。
而对于区间覆盖,我们需要一个结论:我们能发现,在这些颜色段中,对于每个颜色段,只有两端的 \(pre_i\) 才是有价值的,我们不妨称它为有效 \(pre_i\),而有效 \(pre_i\) 的变化数量为 \(O(n+m)\) 级别。我们可以用颜色段均摊的方法证明,对于每次区间覆盖,只会增加一个颜色段,可能还会删除更多的颜色段,因此变化量在 \(O(n+m)\) 级别。
我们就可以用珂朵莉树先对所有修改跑一遍,跑出所有的 \(pre\) 变化。然后 cdq 分治二维数点即可。
[HNOI2010] 城市建设
给定一张图,图有边权,有 \(m\) 次修改一条边的边权,每次修改后输出最小生成树边权和。
数据范围:\(n\le 2\times 10^4, m \le 5\times 10^4\)。
本题个人感觉比上面那题难
本题有常数巨大的线段树分治套 lct 做法,这里不介绍。
暴力肯定是每次询问都跑一次 kruskal,但是复杂度直接爆炸。因此我们考虑简化 kruskal 中边的集合。
我们考虑 \([l, r]\) 这段区间修改的边,不妨把这些边叫做动态边,剩下的边叫做静态边。我们考虑两个极端情况:\(-\infty\) 和 \(+\infty\)。先把动态边的边权全部设为 \(-\infty\),然后跑一遍 kruskal,这时在 MST 中的静态边一定是会被选择的,我们不妨把这些边所对应的点全部缩到一起,这些边也就无用了。
我们再把动态边的边权设为 \(+\infty\) 跑 kruskal,这时不在 MST 中的静态边一定不会在最终的 MST 中,直接扔掉即可。这样我们就完成了简化边集的效果。递归到 \(l=r\) 时把动态边和剩下的边集放一起跑 kruskal 即可。
至于递归顺序,我们可以采用先处理 \([l, r]\),再 \(CDQ(l, mid), CDQ(mid + 1, r)\)。因为我们考虑的是极端情况,而在极端情况之内的普通情况也一定是适用的,所以先处理 \([l, r]\) 再处理左右区间也是正确的。
而对于时间复杂度的分析,我们只需要分析出每一层的复杂度是 \(O(len)\) 相关即可。对于第一个简化边集的操作,至多会剩下 \(len\) 个联通块,因此每个区间要处理的边集也是 \(O(len)\) 级别的。因此复杂度为 \(O(n\log^2n)\)。
其实这题也可以用线段树分治的思想理解。我们在 cdq 分治的过程中其实也建出了一颗线段树,我们上面这题就是对这颗线段树的前序遍历。不过线段树分治可能更好理解 XD。
The End
其实 CDQ 分治我还有一些没写,比如优化斜率优化、四维偏序,但是限于本人能力有限,因此没有写。
标签:偏序,le,询问,分治,笔记,cdq,我们 From: https://www.cnblogs.com/crimsonawa/p/17542010.html