矩阵快速幂优化 DP
用矩阵描述每次转移时 DP 数组的线性变换,如果每次变换转移相同,可以根据矩阵乘法的结合律先快速幂计算出总的转移矩阵。
这里矩阵乘法不只是 \((+,\times)\),实际上只要 \((\oplus,\otimes)\) 满足 \(\otimes\) 对 \(\oplus\) 有分配律,\(\otimes\) 有结合律,\(\oplus\) 有交换律即可。(证明考虑把 \((AB)C=A(BC)\) 这一性质逐步展开)
比较经典的广义矩阵乘法有 \((+,\times),(\max/\min,+),(\gcd,\times)\)。
好像在图上应用比较多。
其他略去不写。
数据结构优化 DP
DP 转移区间修改时,可以考虑放到线段树上进行,类似区间加、区间 \(\max\)、区间推平等操作,可以 \(O(n^k)\) 优化到 \(O(n^{k-1}\log n)\)。
其他略去不写。
单调队列优化 DP
简述
对任意状态和转移复杂度的 DP 都可以优化减少枚举状态中的一维。
要求转移方程形如:
\[f_i=\max_{l_i\le j<i} \{f_j+A_i+B_j\} \]其中 \(A\) 只关于 \(i\) 而 \(B\) 只关于 \(j\),且 \(l_i\) 单调不降,整理后得到:
\[f_i=A_i+\max_{l_i\le j<i} \{f_j+B_j\} \]发现决策点只与其自身有关,且符合滑动窗口的类型,因此可以用单调队列维护出当前决策区间的最优决策点,可以把 \(O(n)\) 枚举优化为 \(O(1)\) 转移。
例题
Luogu-P2569 SCOI2010 股票交易
设 \(f_{i,j}\) 为 \(i\) 天持有 \(j\) 股的最大收益,按照题目要求容易得到:
\[f_{i,j}=\max_{1\le k<i-W,j\le l\le \min(j+AS_i,\mathrm{MaxP})} \{f_{k,l}-(l-j)\times AP_i\} \]\[f_{i,j}=\max_{1\le k<i-W,\max(j-BS_i,0)\le l\le j} \{f_{k,l}+(j-l)\times BP_i\} \]对 \(k\) 的枚举可以前缀 \(\max\) 优化掉,剩下对 \(l\) 的枚举区间分别是 \([j,\min(j+AS_i,\mathrm{MaxP})],[\max(j-BS_i,0),j]\),区间的移动具有单调性,调整枚举顺序即可。
Luogu-P3572 POI2014 PTA-Little Bird
写出转移方程:
\[f_i=\min_{j=i-k}^{i-1} \{f_j+[h_i\ge h_j]\} \]看似无法把转移方程独立成只与 \(j\) 有关,但是每次最多增加 \(1\),因此当 \(f\) 值相等时 \(h\) 值较大的更优,而其余情况 \(f\) 值更小的一定不劣,符合单调性,可以单调队列优化。
斜率优化 DP
简述
解决形如:
\[f_i=\max_{j=0}^{i-1} \{f_j+A_i+B_j+C_i\times D_j\} \]其中 \(A,C\) 只关于 \(i\) 而 \(B,D\) 只关于 \(j\),此时由于 \(i,j\) 共同产生影响,无法独立出 \(j\) 单调队列优化。
一个例题:Luogu-P3195 HNOI2008 玩具装箱。
设 \(f_i\) 为装前 \(i\) 个玩具的最小花费,设 \(s_i=\sum_{j=1}^i (C_i+1)\),可以写出初步转移方程:
\[f_i=\min_{j=0}^{i-1}\{f_j+(s_i-s_j-1-L)^2\} \]为了方便,令 \(L=L+1\),把平方拆开:
\[f_i=\min_{j=0}^{i-1}\{f_j+s_i^2+s_j^2+L^2-2Ls_i+2Ls_j-2s_is_j\} \]按照上面的形式分组:
\[f_i=\min_{j=0}^{i-1}\{f_j+(s_i^2-2Ls_i)+(s_j^2+2Ls_j)-2s_is_j\} \]假设 \(0\le j_1<j_2<i\),我们思考在怎样的条件下,从 \(j_1\) 转移更优。
也就是:
\[f_{j_1}+(s_i^2-2Ls_i)+(s_{j_1}^2+2Ls_{j_1})-2s_is_{j_1}<f_{j_2}+(s_i^2-2Ls_i)+(s_{j_2}^2+2Ls_{j_2})-2s_is_{j_2}< \]\(A\) 部分可以消去,再移项:
\[2s_i(s_{j_2}-s_{j_1})<(f_{j_2}+s_{j_2}^2+2Ls_{j_2})-(f_{j_1}+s_{j_1}^2+2Ls_{j_1}) \]\[2s_i<\dfrac{(f_{j_2}+s_{j_2}^2+2Ls_{j_2})-(f_{j_1}+s_{j_1}^2+2Ls_{j_1})}{s_{j_2}-s_{j_1}} \]不等号右边类似于一个斜率 \((Y_{j_2}-Y_{j_1})/(X_{j_2}-X_{j_1})\) 的形式,也就是如果拿斜率 \(2s_i\) 的直线判断所有的 \(j\),那么第一个满足斜率大于 \(2s_i\) 的点对 \((j_1,j_2)\) 中 \(j_1\) 就是最优决策点。因为显然在这之前的所有点对都是右侧点优于左侧点,而在这之后的所有点对都是左侧点优于右侧点,类似于具有凸性。
现在从线性规划的角度去思考这个问题,我们把转移方程的 \(\min\) 去掉,改为:
\[f_i=f_j+(s_i^2-2Ls_i)+(s_j^2+2Ls_j)-2s_is_j \]这样整理一下:
\[(f_j+s_j^2+2Ls_j)=2s_i\times s_j+(f_i-s_i^2+2Ls_i) \]这符合 \(y=kx+b\) 的直线表达式,且 \(x,y\) 对应的值 \(s_j\) 与 \(f_j+s_j^2+2Ls_j\) 恰好对应上面比较 \(j_1,j_2\) 时的形式。
这样我们相当于是拿斜率为 \(2s_i\) 的直线去切决策点,截距最小的一个点即为最优决策点,此时 \(f_i-s^i2+2Ls_i\) 最小,即 \(f_i\) 最小。
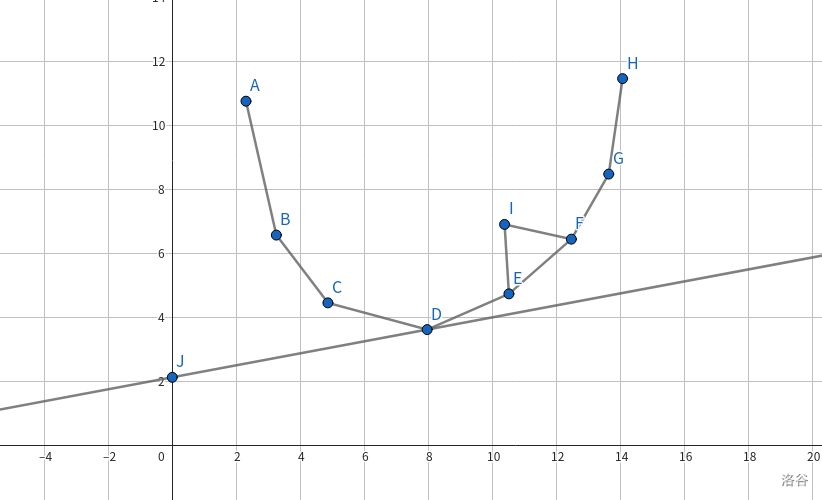
结合上图理解,每个点表示 \([0,i-1]\) 即已经得出 DP 值的位置,容易发现拿直线去切所有决策点时,\(D\) 点的截距最小。
现在问题时如何维护这些决策点,在本题中 \(X_j=s_j\) 单调递增,因此每次都会在右侧增加一个点,考虑点 \((E,F,I)\) 三点的关系,一条任意斜率直线从下向上切 \(I\) 过程中一定会先切到 \(E\) 或 \(F\),也就是说 \(I\) 一定不是决策点,可以扔掉。这就形成了一个凸包。
对于取 \(\min\) 的情况维护下凸包(斜率单调递增),对于取 \(\max\) 的情况就要截距最大,维护上凸包(斜率单调递减)。
后面的内容均以取 \(\min\) 为例子讨论。
\(X\) 与斜率 \(k_i\) 均具有单调性的情况
即当一段 \((j_1,j_2)\) 斜率小于当前的斜率后就不可能再作为转移点,即判断 \(\mathrm{slope}(j_1,j_2)\le k_i\)。
在右侧加入新的点 \(i\) 时不断弹出直到找到第一段 \((j_1,j_2)\) 满足 \(\mathrm{slope}(j_1,j_2)<\mathrm{slope}(j_2,i)\),将 \(i\) 加入。
后者的操作就是单调栈维护凸包,由于前者的操作具有单调性,使用单调队列。
每次完成前者操作后,队首即为最优决策点。
时间复杂度 \(O(n)\)。
只有 \(X\) 具有单调性的情况
维护凸包的部分同样是单调栈操作,只不过查询不具有单调性不能扔掉当前无用决策点,但每次单调栈二分即可。
时间复杂度 \(O(n\log n)\)。
没有任何单调性
动态凸包?李超线段树?不会。
一些注意点
-
在队首弹出无用决策点或是二分决策点时,判断斜率是否取等并不重要,因为平行的直线切在任何一个点上截距都不变。
-
在单调栈保持凸包斜率单调性时,应当保证凸包斜率严格单调,即当且仅当 \(\mathrm{slope}(j_1,j_2)<\mathrm{slope}(j_2,i)\) 才停止弹栈。
-
关于精度问题使用
long double可以避免绝大多数问题,但是一些题目中会出现 \(X\) 不严格单调递增的情况,此时 \(X_{j_1}=X_{j_2}\) 是我们在计算斜率是不想看到的。一个简单的处理是:
例题
Luogu-P5785 SDOI2012 任务安排
维护结束时间是困难的,考虑拆开贡献,如果一批任务为 \([l,r]\),用时为 \(s+\sum_{i=l}^r t_i\),那么 \([l,n]\) 的结束时间都会增加这个值,将贡献提前计算。
设 \(st_i=\sum_{j=1}^i t_j,sc_i=\sum_{j=i+1}^n c_j\),得到转移方程:
\[f_i=\min_{j=0}^{i-1} \{f_j+(st_i-st_j+s)\times sc_{j}\} \]拆开整理成:
\[f_j-(st_j-s)\times sc_j=st_i\times (-sc_j)+f_i \]这样保证 \(X=-sc_j\) 是单调不降的,\(t\) 可能为负,斜率 \(st_i\) 单调性不保证,因此单调栈维护凸包并二分。
长链剖分优化 DP
见 长链剖分学习笔记,主要是优化了转移方程设计仅与深度有关的 DP。
参考资料
单调队列优化 DP
-
OI-Wiki