李超线段树 学习笔记
今天模拟赛用到了李超线段树(但是本蒟蒻费了半天劲搞了个斜率优化拿到了 60pts 的好成绩 /kk),所以学习一下李超线段树刻不容缓(学会了我貌似也切不来那道题 qwq)。
引入
初中和高中我们都做过函数题吧,是不是有时候给你两根甚至几根直线,然后问你某个点的最值?当然,直线数很少的时候我们很容易做,甚至可以直接画图来看。现在我们要用计算机来解决这个问题,但是计算机可不会看图……怎么办呢?李超线段树出来力!
李超线段树是巨佬李超发明的一种数据结构,能在 \(\log_n\) ( \(n\) 为定义域大小,当然也可以通过动态开点来搞掉,不过都是后话了)的复杂度下求出几个一次函数在某一横坐标下,纵坐标的最大值。
思想
好吧李超线段树的思想其实也不是很复杂,简而言之就是,我们在每个节点(也就是区间)上,维护一条优势线段,其中优势线段的“优势”体现在区间中点处,也就是它在中点处能取到该点所有直线的最大纵坐标。
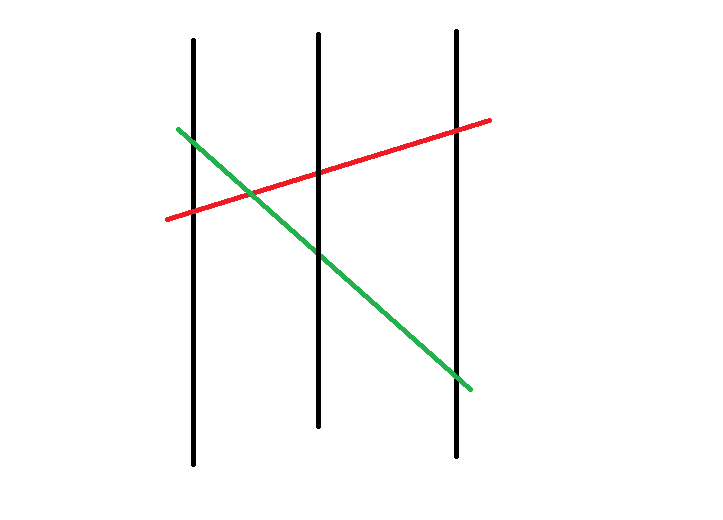
我们结合图来理解一下:
上图中,红色线段就是一条优势线段。
然后我们来考虑一下如何插入——
对于一个区间 \([l, r]\),我们要插入线段(直线) \(a\),分如下几种情况:
- 该区间没有线段,那么直接覆盖即可;
- 该区间已经有线段,但是 \(a\) 的左右端点都比原线段高,那么新线段就是优势线段,也是直接覆盖即可;
- 该区间已经有线段,而 \(a\) 的左右端点都比原线段低,那么就不作修改;
- 该区间已经有线段,而 \(a\) 与原线段 \(b\) 在区间内有交点,我们就讨论交点的位置:
- 如果交点在区间中点左侧(如上图),我们令中点处值较大的一条线段为优势线段。由于交点在中点左侧,所以在右半个区间中,优势线段仍然不会改变,所以不用修改;由于我们不能确定左侧区间内优势线段是谁,所以我们将非优势线段传递下去,修改左侧即可。
- 交点在区间中点右侧同理,只不过要继续修改的变成区间右侧。
那我们如何查询呢?
对于每个点的询问,我们必须要把包含该点的所有区间询问一次,取最大值。为什么呢?考虑这样一个问题:我们传递修改的过程中,只是把非优势线段传递下去,但是优势线段是无法下放的。也就是说,我们每个区间只是维护了一个相对优势的线段,来保证答案可能从中产生,而最终答案必须是从上往下都算一遍的。
例题
[洛谷 P4254 Blue Mary 开公司](P4254 [JSOI2008] Blue Mary 开公司 )
板子题,也没有啥细节,正好借这个题把板子总结一下。
代码:
#include<bits/stdc++.h>
#define ls tr<<1
#define rs tr<<1 | 1
#define LD long double
using namespace std;
const int N = 1e5+100, D = 5e4+100;
struct Line{
double k, b;//y = kx+b;
int l, r;//注意这里的l,r并不是记录区间的左右端点,而是记录线段的左右端点,这道题的线段都是直线,但是某些题需要对线段进行处理。
int flag;//标记区间有无线段。
}tree[N<<2];
int n, tot;
double calc(int x, Line tmp){
return tmp.k*x+tmp.b;
}//计算某个点的纵坐标值。
int cross(Line a, Line b){
return (b.b-a.b)/(a.k-b.k);
}//计算中点横坐标。
void build(int tr, int L, int R){
tree[tr] = {0, 0, 1, 50000, 0};//预处理。
if(L == R) return;
int mid = (L+R)>>1;
build(ls, L, mid);
build(rs, mid+1, R);
}
void modify(int tr, int L, int R, Line tmp){
if(tmp.l<=L && R<=tmp.r){//首先判断线段是否包含区间[L, R]。
if(!tree[tr].flag) tree[tr] = tmp, tree[tr].flag = 1;//情况1,直接覆盖。
else if(calc(L, tmp)>calc(L, tree[tr])&&calc(R, tmp)>calc(R, tree[tr])) tree[tr] = tmp;//情况2,覆盖。
else if(calc(L, tmp)>calc(L, tree[tr]) || calc(R, tmp)>calc(R, tree[tr])){//情况4
int mid = (L+R)>>1;
if(calc(mid, tmp)>calc(mid, tree[tr])){
swap(tree[tr], tmp);
}
if(cross(tmp, tree[tr])<=mid) modify(ls, L, mid, tmp);
else modify(rs, mid+1, R, tmp);
}
}else{//这一线段并不能代表区间内的情况,故要传递下去。
int mid = (L+R)>>1;
if(tmp.l<=mid) modify(ls, L, mid, tmp);
if(mid<tmp.r) modify(rs, mid+1, R, tmp);
}
}
double query(int tr, int L, int R, int x){//每走到一个区间就取一遍,求最大值。
if(L == R) return calc(x, tree[tr]);
int mid = (L+R)>>1;
double ans = calc(x, tree[tr]);
if(x <= mid) return max(ans, query(ls, L, mid, x));
else return max(ans, query(rs, mid+1, R, x));
}
char op[10];
int main(){
scanf("%d", &n);
build(1, 1, 50000);
while(n--){
scanf("%s", op);
if(op[0]=='Q'){
int day;
scanf("%d", &day);
int ans = ((int)query(1, 1, 50000, day))/100;
printf("%d\n", ans);
} else{
Line tmp;
scanf("%lf%lf", &tmp.b, &tmp.k);
tmp.l = 1, tmp.r = 50000;//这道题只对直线进行处理,所以左右端点可以看作定义域左右端点。
tmp.b-=tmp.k;
modify(1, 1, 50000, tmp);
}
}
return 0;
}