最好有小学六年级的数学水平(doge)。
基础拉格朗日插值
我们先了解最简单的拉格朗日插值可以干什么。
由小学知识可知 \(n\) 个点 \((x_i,y_i)\) 可以唯一地确定一个多项式 \(y = f(x)\)。
现在,给定这 \(n\) 个点,请你确定这个多项式。
第一眼,我们很容易想到可以使用高斯消元法在 \(O(n^3)\) 的时间内求解。但是拉格朗日插值可以做到 \(O(n^2)\) 甚至 \(O(n \log^2 n)\) 。我们这里讲解 \(O(n^2)\) 的插值。
为了举个例子,我们需要对以下四个点求出函数值:
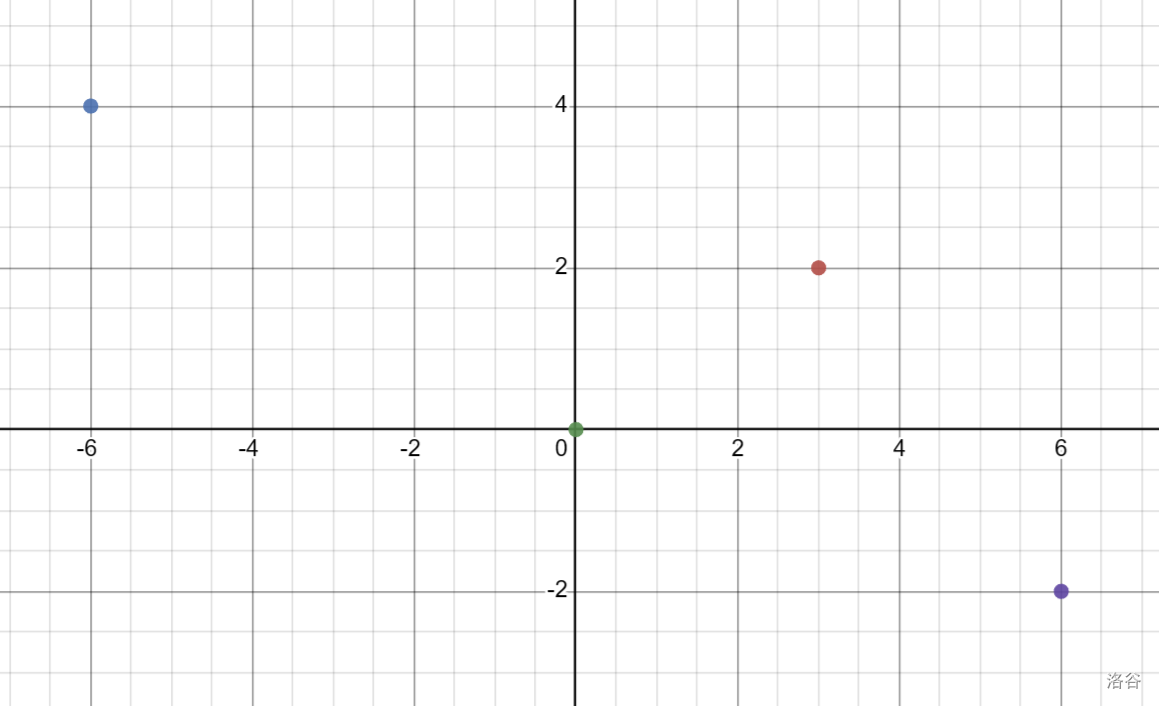
我们考虑构造 \(4\) 个基函数,期中,第 \(i\) 个基函数需要满足对于第 \(i\) 个点,函数值为 \(1\) ,其余点,函数值都为 \(0\) 。怎么构造这个基函数呢?我们拿第一个点 \((-6,4)\) 来说,如果第三个点 \((3 2)\) 要在 \(x=3\) 时 \(y=0\) ,那么我们可以为这个基函数构造 \((x-3)\) 项,这样子就会一定满足条件。我们很容易构造出基函数 \(f_1\) :
\[f_1(x)=c\times x(x-3)(x-6) \]我们对于 \(x=-6\) 时需求 \(f_1(x)=1\) ,那么有:
\[c=\dfrac{1}{x(x-3)(x-6)}=\dfrac{1}{-6 \times (-9) \times (-12)}=\dfrac{1}{-648} \]所以有:
\[f_1(x)=\dfrac{1}{-648}x(x-3)(x-6) \]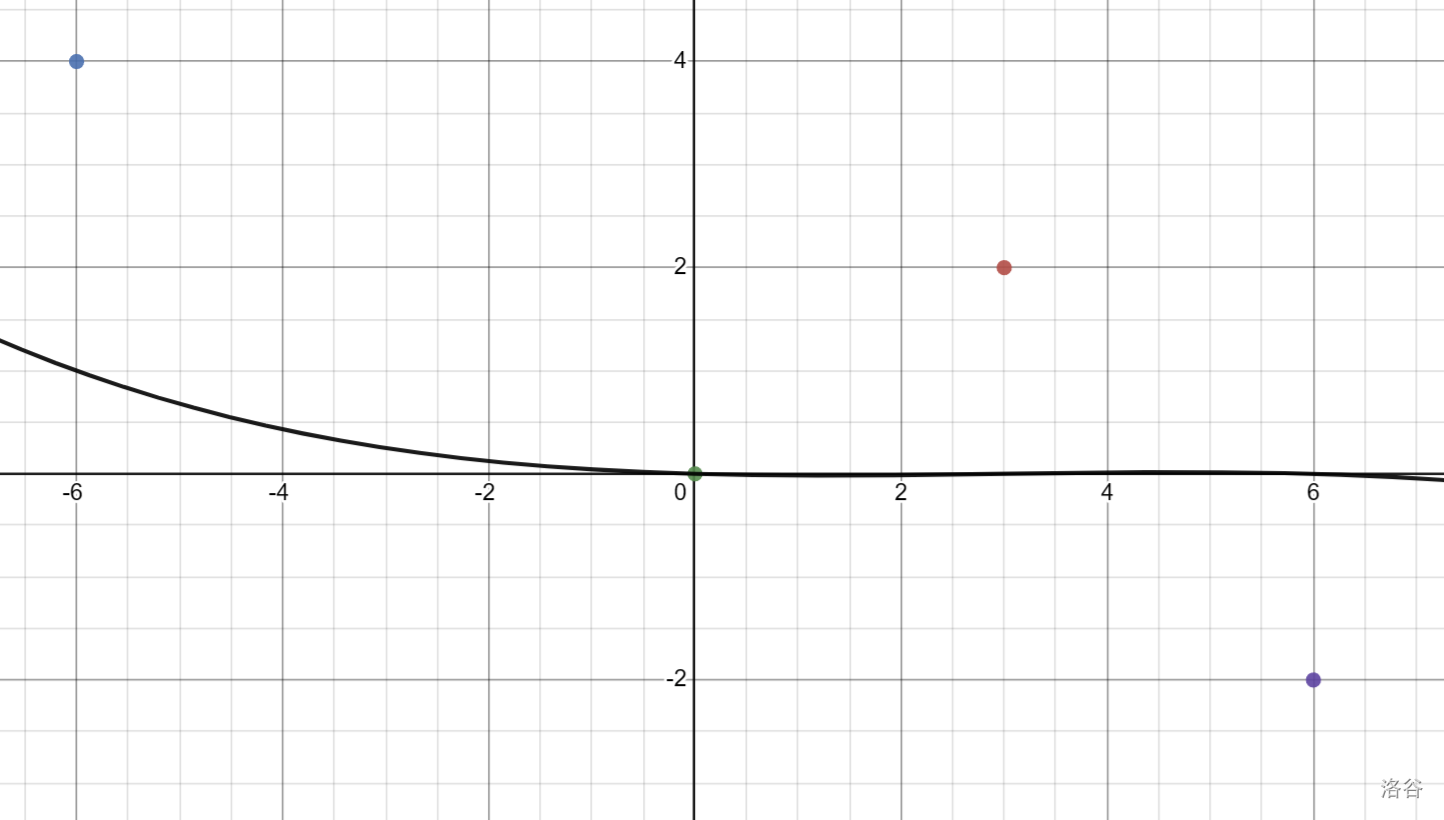
类似的,我们可以得到另外的基函数 \(f_2,f_3,f_4\) 。但是这样我们怎么得到最终的函数呢?
\[f(x)=\sum_{i=1}^n y_if_i(x) \]因为这个函数时一定满足我们需求的,对于给定的 \(n\) 个点之一的 \((x_i,y_i)\) ,它只有在循环到 \(i\) 时, \(y_if_i(x_i)=y_i\) 有值,其余时刻按照基函数的定义都为 \(0\) 。所以这十分合理。我们可以改写成公式的形式:
\[f(x)=\sum_{i=1}^n y_i \prod_{j=1,j \neq i} \dfrac{x-x_i}{x_i-x_j} \]贴出一份封装了 $namespace $ 的代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-f;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
const int mod=998244353;
const int MAXN=2e3+10;
namespace Lagrange{
int qpow(int a,int b){
int ans=1,base=a;
while(b){
if(b&1) ans=ans*base%mod;
base=base*base%mod;
b>>=1;
}
return ans;
}
int inv(int x){
return qpow(x,mod-2);
}
int lagrange(int n,int *x,int *y,int k){
int ans=0;
for(int i=1;i<=n;i++){
int top=1,down=1;
for(int j=1;j<=n;j++){
if(j==i) continue;
top=top*((k-x[j]+mod*2)%mod)%mod;
down=down*((x[i]-x[j]+mod*2)%mod)%mod;
}
ans=(ans+y[i]*top%mod*inv(down))%mod;
}
return ans;
}
}
using namespace Lagrange;
int n,x[MAXN],y[MAXN],k;
signed main(){
n=read(),k=read();
for(int i=1;i<=n;i++) x[i]=read(),y[i]=read();
cout<<lagrange(n,x,y,k);
return 0;
}