2022-2023 春学期 矩阵与数值分析 C6 插值函数的应用
C6 插值函数的应用
6.1 插值型求积公式
数值型求积公式
用于解决难以找到原函数的积分问题
问题描述:设 \(f(x)\) 是定义在 \([a,b]\) 上的可积函数,考虑带权积分
\[I(f)=\int^b_a\rho(x)f(x)dx \]其中权函数 \(\rho(x)\) 在 \([a,b]\) 上非负可积,且至多有有限个零点
数值求积:用
\[I_n(f)=\sum\limits^n_{k=0}A_kf(x_k) \]近似计算 \(I(f)\) 的值,其中 \(A_k(k=0,1,\cdots,n)\) 是与 \(f(x)\) 无关的常数,称为求积系数,\([a,b]\) 上的点 \(x_k(k=0,1,\cdots,n)\) 称为求积节点
几种数值求积公式:
- 左矩形数值求积公式:\(\int^a_bf(x)dx\approx f(a)(b-a)\)
- 右矩形数值求积公式:\(\int^a_bf(x)dx\approx f(b)(b-a)\)
- 中矩形数值求积公式(精度为1):\(\int^a_bf(x)dx\approx f(\frac{a+b}{2})(b-a)\)
- 梯矩形数值求积公式(精度为1):\(\int^a_bf(x)dx\approx \frac{(b-a)}{2}[f(a)+f(b)]\)
通常,插值型求积公式可以表示为插值多项式和余项的和的形式
\[I(f)=I_n(f)+E_n(f) \]\[\int^a_bf(x)dx=\sum\limits^n_{k=0}A_k\cdot f(x_k)+\int^b_ar_n(xdx) \]Newton-Cotes 公式
Newton-Cotes 公式:插值型求积公式
\[I_n(f)=\sum\limits^n_{k=0}A_k\cdot f(x_k) \]称为 n+1 点的 Newton-Cotes 公式,其中求积系数
\[A_k=\int^b_al_k(x)dx\quad k=0,1,\cdots,n \]在 Newton-Cotes 公式中,求积节点间的距离通常是相等的,与 Gauss 型求积公式不同
求积余项:\(E_n(f)=\int_a^br_n(x)dx=\int_a^b\frac{f^{(n+1)}(\xi_x)}{(n+1)!}w_{n+1(x)}dx\) 标志着求积公式的误差大小
常用的 Newton-Cotes 有:
-
n=1,两点,梯形公式
\[I_1(f)=A_0f(a)+A_1f(b)=\frac{(b-a)}{2}(f(a)+f(b)) \] -
n=2,三点,Simpson 求积公式
\[I_2(f)=A_0f(a)+A_1f(\frac{(a+b)}{2})+A_2f(b)=\frac{(b-a)}{6}(f(a)+4\times f(\frac{(a+b)}{2})+f(b)) \] -
n=4,五点,Cotes 公式
\[I_4(f)=\frac{(b-a)}{90}(7f(a)+32f(x_1)+12f(x_2)+32f(x_3)+7f(b)) \]
n+1 点 Newton-Cotes 公式有如下特点对称性/单位分解性;等距节点的 Largrange 插值基函数满足单位分解性
\[\sum\limits^n_{i=0}l_i(x)=1 \]N-C 公式的求积系数是对称的,并且满足单位分解性
\[\sum\limits^n_{k=0}A_k=\sum\limits^n_{k=0}\int^b_al_k(x)dx=\int_a^b\sum\limits^n_{k=0}l_k(x)dx=\int^b_a1dx=b-a \]例题

代数精度与求积余项
代数精度用于衡量数值求积公式的精度,可以从求积余项得到代数精度;代数精度都是“粗”的误差估计,求积余项是“细”的误差估计
代数精度:若某数值求积公式对任何次数不超过 m 的代数多项式精确成立
\[I(p_m(x))=\int^b_ap_m(x)dx\equiv\sum\limits^n_{k=0}A_k\cdot p_m(x_k)=I_n(p_m(x)) \]但对于 m+1 次代数多项式不一定能准确成立,即
\[I(p_{m+1}(x))=\int^b_a p_{m+1}(x)dx\neq\sum\limits^n_{k=0}A_k\cdot p_{m+1}(x_k)=I_n(p_{m+1}(x)) \]则称该求积公式具有 m 次代数精度
数值求积公式具有 m 次代数精度的充要条件是它对 \(f(x)=1,x,\cdots,x^m\) 都能准确成立,但对 \(x^{m+1}\) 不能准确成立。
n+1 个节点的求积公式,代数精度至少为 n,至多为 2n+1,必小于 2n+2
Newton-Cotes 公式的代数精度:
- 当 n 为偶数时,n+1 点的 Newton-Cotes 公式的代数精度为 n+1
- 当 n 为奇数时,n+1 点的 Newton-Cotes 公式的代数精度为 n
也就是,n+1 点 Newton-Cotes 公式至少有 n 次代数精度;并且,代数精度只能是奇数
梯形公式、Simpson 公式、Cotes 公式的代数精度分别为 1,3,5;如同下表所示
| n=1 | m=1 |
|---|---|
| n=2 | m=3 |
| n=3 | m=3 |
| n=4 | m=5 |
| n=5 | m=5 |
Newton-Cotes 公式的求积余项:一般对 n+1 点 Newton-Cotes 公式的求积余项,有如下定理:
- n 是偶数,且 \(f(x)\in C^{n+2}[a,b]\),则 \(E_n(f)=C_nh^{n+3}f^{(n+2)}(\eta),\quad \eta\in(a,b)\),其中 \(C_n=\frac{1}{(n+2)!}\int^n_0t^2(t-1)\cdots(t-n)dt\)。
- n 是奇数,且 \(f(x)\in C^{n+1}[a,b]\),则 \(E_n(f)=C_nh^{n+2}f^{(n+1)}(\eta),\quad \eta\in(a,b)\),其中 \(C_n=\frac{1}{(n+1)!}\int^n_0t^(t-1)\cdots(t-n)dt\)。
例子
对梯形公式(1 次代数精度)有:

对 Simpson 公式(3 次代数精度)有:

梯形公式的求积余项

Simpson 公式的求积余项


1

复化求积公式
将大区间分割成若干小区间,在小区间内使用 Newton-Cotes 求积公式,改善稳定性和收敛性
复化求积公式不会提高代数精度
具体的做法:将 \([a,b]\) 等分成若干个小区间 \([x_k,x_{k+1}]\;(k=0,1,\cdots,n-1)\) 有
\[\int^b_af(x)dx=\sum\limits^{n-1}_{k=0}\int^{x_{k+1}}_{x_{k-1}}f(x)dx \]在每个小区间上用点数少的 Newton-Cotes 公式进行数值积分,这样得到的数值求积公式称为复化 Newton-Cotes 公式
复化梯形公式:
\[T_n=\frac{b-a}{2n}[f(a)+2\sum\limits_{k=1}^{n-1}f(x_k)+f(b)] \]复化 Simpson 公式:
\[S_n=\frac{b-a}{6n}[f(a)+2\sum\limits_{k=1}^{n-1}f(x_k)+4\sum\limits^{n-1}_{k=0}f(x_{k+\frac{1}{2}})+f(b)] \]复化 Cotes 公式:
\[C_n=\frac{b-a}{90n}[7f(a)+32\sum\limits_{k=1}^{n-1}f(x_{k+\frac{1}{4}})+12\sum\limits_{k=1}^{n-1}f(x_{k+\frac{1}{2}})+32\sum\limits_{k=1}^{n-1}f(x_{k+\frac{3}{4}})+14\sum\limits_{k=1}^{n-1}f(x_{k})+7f(b)] \]*复化求积公式的余项估计


例题

6.2 Gauss 型求积公式
改进了 Newton-Cotes 中等距节点的取法,从而获得更高的代数精度
概念
定义:如果求积公式具有代数精度 2n+1,则称其为 Gauss 型求积公式,并称其中的求积节点 \(x_k(k=0,1,\cdots,n)\) 为 Gauss 点
具体的做法:对于数值求积公式:
\[\int^{1}_{-1}f(x)dx=A_0f(x_0)+A_1f(x_1) \]由代数精度的定义可得如下线性方程组
\[\left\{ \begin{array}{l} A_0+A_1=2\\ A_0\cdot x_0+A_1\cdot x_1=0\\ A_0\cdot x_0^2+A_1\cdot x_1^2=\frac{2}{3}\\ A_0\cdot x_0^3+A_1\cdot x_1^3=0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} A_0=A_1=1\\ x_0=\frac{-1}{\sqrt{3}},\;x_1=\frac{1}{\sqrt{3}} \end{array} \right. \]即
\[\int^1_{-1}f(x)dx\approx f(-\frac{1}{\sqrt{3}})+f(\frac{1}{\sqrt{3}}) \]实用构造方法
求积节点:要是插值型求积公式
\[\int^b_a\rho(x)f(x)dx=\sum\limits^n_{k=0}A_kf(x_k)+E_n(f) \]具有 2n+1 次精度,必须且只须以节点 \(x_0,x_1,\cdots,x_n\) 为零点的 n+1 次求积多项式
\[\omega_{n+1}(x)=\prod^n_{j=0}(x-x_j) \]与所有次数不超过 n 的多项式在 \([a,b]\) 上关于权函数 \(\rho(x)\) 正交
也就是有:
- \(x_0,x_1,\cdots,x_n\) 是高斯点 \(\Leftrightarrow\) \(\omega_{n+1}(x)\)是正交多项式
- \(x_0,x_1,\cdots,x_n\) 是高斯点 \(\Leftrightarrow\) \(x_0,x_1,\cdots,x_n\) 是正交多项式的根
求积系数:Gauss 型求积公式
\[\int_a^bf(x)\approx \sum\limits^n_{k=1}A_kf(x_k) \]求积系数 \(A_k=\int_a^b\rho(x)(\frac{\omega_{n+1}(x)}{\omega'_{n+1}(x_k)(x-x_k)})^2dx\quad x_0,x_1,\cdots,x_n\) 是正交多项式的根,也可按照 Lagrange 插值公式构造求积系数
\[A_k=\int_a^b\rho(x)(\frac{\omega_{n+1}(x)}{\omega'_{n+1}(x_k)(x-x_k)})dx \]求积系数具有如下的性质:
-
Gauss 型求积公式的所有求积系数均为正数,即 \(A_k>0,\;k=0,1,\cdots,n\),且 \(\sum\limits^n_{k=1}A_k=\int_a^b\rho(x)dx\)
- \[ A_k=\int_a^b\rho(x)l_k(x)dx=\int_a^b\rho(x)l^2_k(x)dx \]
*求积余项

*数值稳定性和收敛性

做题构造方法-例题
构造两点的 Gauss 型求积公式,更多点的同理,使用需要构造更高次的正交多项式;不同区间、权函数的也类似,只需修改构造正交多项式时求解系数的积分的区间、权函数即可


可通过变量替换的方式,求出其他区间上具有相同权函数的 Gauss 型求积公式
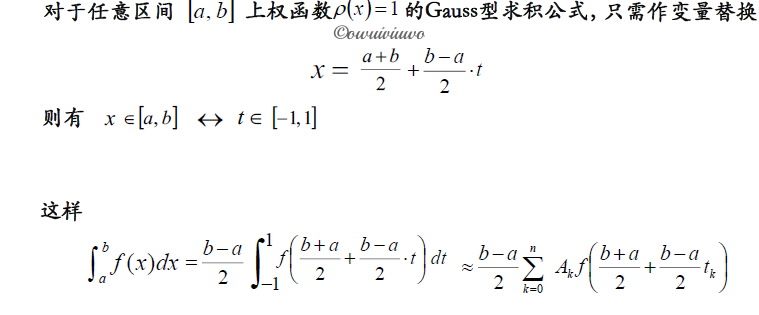

1

2


3



4

