目录
- 0.「UR #9」「UOJ #133」电路手动分析
- 1.「UR #9」「UOJ #134」App 管理器
- 2.「UR #10」「UOJ #152」汉诺塔
- 3.「UNR #2」「UOJ #312」梦中的题面 ⭐
- 4.「NOI Simu.」战舰
- 5.「UR #10」「UOJ #153」世界线 ⭐
- 6.「洛谷 P9411」Gtrimee
- 7.「CF 1500F」Cupboards Jumps ⭐
- 8.「UR #11」「UOJ #167」元旦老人与汉诺塔
- 9.「NOI Simu.」高维游走 ⭐
- 10.「NOI Simu.」过山车 ⭐
- 11.「NOI Simu.」木棍 ⭐
- 12.「UR #11」「UOJ #169」元旦老人与数列 ⭐
- 13.「UR #12」「UOJ #180」实验室外的攻防战
- 14.「UR #13」「UOJ #186」Yist
- 15.「UR #13」「UOJ #187」Ernd ⭐
Umm… UOJ 浓度极高的一个 sol set. 摘的标题和上一个 sol set 是姊妹篇!
0.「UR #9」「UOJ #133」电路手动分析
- Link & Submission.
二分答案, 尽量把选择的结点排成正方形, 计算边数够不够. \(\mathcal O(\log\min\{nm,\sqrt r\})\).
1.「UR #9」「UOJ #134」App 管理器
- Link & Submission.
枚举未定向边 \((u,v)\), 检查去掉这条边后是否存在 \(u\to v\) 或 \(v\to u\) 的路径, 二者中至少存在一个, 据此定向即可. \(\mathcal O(m^2)\).
2.「UR #10」「UOJ #152」汉诺塔
- Link & Submission.
- 「A.构造」
你这 \(10^6\) 的操作限制是来骗人的还是来骗兔的?
如何利用 \(2,3\) 两根空柱子? 把 \(1\) 柱子上的盘子依次取出放入 \(2,3\) 之一的过程可以看作对 \(1\) 柱子序列的一个划分, 结合排序的目标, 那么自然想到上升/下降子序列. 假设 \(1\) 从上到下读可以划分为 \(k\) 个连续的上升子段, 我们就可以把它们倒到 \(2,3\) 上, 在两根柱子上各形成 \(k/2\) 个下降子段. 每次取出两个柱子最顶上的子段归并回 \(1\), 子段数量 \(\div2\). 因此 \(\mathcal O(\log n)\) 次迭代后必然完成排序. 操作次数 \(\mathcal O(n\log n)\).
3.「UNR #2」「UOJ #312」梦中的题面 ⭐
- Link & Submission.
- 「A.DP-数位 DP」
数位 DP? 啊, 数位 DP!
在 \(c=1\) 时, \(x_i\) 就是 \(b\) 进制下的任意 \(i\) 位数, 由于 \(m\) 个 \(b\) 进制数的加法在某一位上的总进位不超过 \(m\), 我们可以暴力记录仅考虑低若干位时, \(\sum x_i-n\) 在当前位的值. 对 \(c=0\), 直接新增一维状态记录有多少个在当前位可以非 \(0\) (而非留到最高位变成 \(x_i=b^i\)) 即可. 最后的状态就是 \(f(i,j,k)\) 表示考虑了第 \(i\) 位, 有 \(j\) 个数可以自由填位, 当前位 \(\sum x_i-n=k\in[-1,m]\) 的方案数. 直接转移可以做到 \(\mathcal O(m^4b)\). 如果从高位向低位 DP 可以得到四方做法, 不过写着比较麻烦.
4.「NOI Simu.」战舰
-
Private link | 卡常, 再见!
-
「B.复杂度平衡」
横纵坐标上的操作相对独立, 我们可以对每一个横坐标维护其一列上的信息, 纵坐标同理. 移动什么的可以直接合并坐标, 加法和查询按照行列长度根号平衡就行了. \(\mathcal O(m\sqrt n)\). 可能有一些很 dirty 的实现细节.
5.「UR #10」「UOJ #153」世界线 ⭐
- Link & Submission.
- 「A.构造」
对于左侧的下标集合 \(S\), 我们尝试找到其在右侧对应的集合 \(\{a_i\mid i\in S\}\). 我们可以把左侧连成若干个大小两两不等的连通块, 再在右侧询问出每个连通块, 这样就能根据连通块大小得到对应关系. 为了得到更确定的对应, 自然的 motivation 就是尝试让左侧集合大小两两不同. 我们可以将左侧标号分组:
\[\begin{array}{c|cccc} & 4 & 3 & 2 & 1 \\ \hline 1 & 1 \\ 2 & 2 & 3 \\ 3 & 4 & 5 & 6 \\ 4 & 7 & 8 & 9 & 10 \end{array} \]可以发现, 左侧的行长度和上侧的列长度构成的坐标可以唯一确定一个单元, 我们就能根据右侧集合所在的行列长度信息直接得到答案.
这个构造只在 \(n=k(k+1)/2\) 时适用, 当 \(n\neq k(k+1)/2\), 我们不可能让行列长度都两两不等, 怎么办呢?
反思一下, 连通块询问带给我们的信息只有 "连通块大小"? 并不是, 我们还可以知道任意两个右侧元素是否在同一连通块, 只不过单用这个信息没办法形成对应关系, 所以在刚刚的构造中没有起作用. 这里有 key motivation: 如果存在且仅存在一个行 (列) 连通块大小为 \(1\), 我们可以直接确定某个 \(a_p\), 然后根据 \(a_p\) 和哪些元素在同一个连通块里确定 \(p\) 这一列 (行) 的集合. 这样, 就算两列 (行) 的长度本来相同, 我们也可以根据特殊元素 \(a_p\) 来区分它们!
给出对 \(n=k(k+1)/2+r~(r\neq 0)\) 的构造, 这里以 \(n=13\) 为例:
\[\begin{array}{c|cccc:c} & 4 & 3^\star & 2^\star & 1 & 1\\ \hline 1 & 1\\ 2 & 2 & 3\\ 3 & 4 & 5 & 6\\ 4 & 7 & 8 & 9 & 10\\ \hdashline 3 & & 11 & 12 & & 13 \end{array} \](\(k^\star=k+1\) 表示自然数 \(k\) 的后继, 这样表格好看一点.)
仍然在两次实验中分别划分行和列询问. 求答案时, 先根据 "行长为 \(r\) (只有两行) 且列长为 \(1\) (另一行上不可能存在列长为 \(1\))" 确定 \(a_n\). 然后根据 "和 \(a_n\) 属于同一行连通块, 列长依次递减" 得到 \(n-r+1\sim n\) 和 \(a_{n-r+1\sim n}\) 的所有对应. 接着令 "和某个 \(a_i~(i\in[n-r+1,n])\) 同属一个列连通块" 的元素列长 \(-1\), 这样就完全消除了最外圈一行一列的影响, 剩下的就和 \(r=0\) 一样做了. 加边 \(2\times\mathcal O(n)\) 次, 询问 \(2\times\mathcal O(n\sqrt n)\) 次.
怎么办, 越来越喜欢构造题了.
6.「洛谷 P9411」Gtrimee
- Link | 胡.
Para 怎么问了兔一个经典 trick? 原来 Para 又在卷洛谷的比赛. Para AK 了, 比赛 unrated 了, 可喜可贺.
GF 入门训练, 先求出任意有根儿子有序无标号树的 GF \(F(z)\) (哈哈! 天下谁人不识 Catalan 数?), 则所求树第 \(k\) 层结点的子树 GF 是 \(F(z)-1\), 再进行 \(k\) 次和求 \(F(z)\) 一样的迭代就行. 这里的迭代是
\[F^\star(z)=\frac{z}{1-F(z)}. \]很显然, 令 \(F(z)=P(z)/Q(z)\), 这个迭代一次就是对 \(\begin{bmatrix}P(z)&Q(z)\end{bmatrix}^T\) 的线性变换:
\[\begin{bmatrix} P^\star(z)\\ Q^\star(z) \end{bmatrix} = \begin{bmatrix} &z\\ -1&1 \end{bmatrix} \begin{bmatrix} P(z)\\ Q(z) \end{bmatrix}. \]矩阵快速幂即可. \(\mathcal O(n\log n\log k)\). 快速幂的结果也可以直接解出来, 这样是 \(\mathcal O(n\log n)\) 的.
7.「CF 1500F」Cupboards Jumps ⭐
- Link & Submission.
- 「A.DP-数据结构优化」
感觉兔的思维习惯变得 contructive & mathematical 了, 根本不会做 OI 题. (雾
DP! DP! DP! 好看起见, 原题的 \(h,w\) 分别换成 \(a,b\). 令 \(f(i,j)\) 表示构造 \(a[:i]\) 使得 \(b[:i-2]\) 合法时, \(|a_i-a_{i-1}|=j\) 是否可行. 转移:
\[f(i+1,b_{i-1}-j)\oreq f(i,j)\quad (j<b_{i-1}),\\ f(i+1,b_{i-1})\oreq f(i,j)\quad (j<b_{i-1}),\\ f(i+1,k)\oreq f(i,j)\quad (j=b_{i-1},\forall k\le b_{i-1}). \]注意第三类转移是覆盖性的 "全部合法", 第一类转移是整体位移, 第二类转移只会新增单点. 初始状态 \(f(0,\cdot)=\textbf T\) 可以表示为一段足够长的区间, 进而我们可以通过维护大区间和小单点的位移来快速实现转移. 利用状态信息反向构造方案即可. \(\mathcal O(n\log n)\).
8.「UR #11」「UOJ #167」元旦老人与汉诺塔
- Link & Submission.
直觉上有种怪异感, 理论上任意两个合法状态都是可达的, 但步数是指数级别, 合法状态的数量也是指数级别, 我们还要计数而非找最优解. 怎么回事呢?
那就只能看 \(m\) — 如果称 \(m\) 是可接受的 "线性" 级别, 那么真正被移动的盘子就只能是 "对数" 级别.
顺着这个思路发现, 初始状态实际上只有 \(3\log_2m\) 个盘子是可能被移动的, 暴力记搜的状态空间是 \(\mathcal O(m3^{3\log_2m})=\mathcal O(m^{1+3\log_23})\), 当然这只是毛估, 真正有效状态量自然很少, 能过就对啦.
9.「NOI Simu.」高维游走 ⭐
- Private link & Submission.
- 「A.DP-状压/插头 DP」
先不考虑疲倦度, 我们先对一个确定的步数序列 \(\{a_m\}\) 描述答案, 其中 \(a_i\) 即在第 \(0\) 阶段 (和第 \(i\) 阶段) 的行走步数, 那么这种方案对 \(f(\cdot)\) 的贡献为
\[\binom{t_0}{\{a_n\}}\prod_{i=1}^n\binom{t_i}{a_i}\equiv[\forall i\neq j,~a_i\cap a_j=\varnothing][\forall i,~a_i\subseteq(t_i\cap t_0)]\pmod2. \]这里数的集合运算即对其二进制所表示的集合的运算.
这一基本的性质告诉我们, 我们只需要考虑满足等式右侧真值式的 \(\{a_n\}\). 一个 \(\{a_n\}\) 将贡献到 \(x=\sum_ii\cdot a_i\) 的 \(f(x)\). 由于 \(\{a_n\}\) 间两两交集为空这个限制很难在依次枚举 \(a_i\) 时记录, 我们更倾向于按位考虑贡献. 设 \(p_i\) 表示第 \(i\) 个 bit 出现在哪个 \(a\) 中, 若未出现则令 \(p_i=0\). 那么 \(x=\sum_ip_i2^i\). 据此, 我们得到了一个暴力做法: 枚举所有可能的 \(\{p_w\}\), 统计出现奇数次的 \(x\) 的个数.
都说啦, 我们倾向于按位考虑贡献. 当只考虑 \(\{p_{0..k-1}\}\) 时, \(x\) 的低 \(k\) 个 bit 已经确定, 此时 \(x\) 剩下的 bit 构成的数在 \([0,m]\) 内, 这就产生了对 \(x\) 的分类标准. 注意, 我们的最终目标是统计 "同一个 \(x\) 出现奇数次" 的数量, 所以这里应该按照 "未确定的长成什么样子" 来划分状态. 设 \(f(k,S)\) 表示 {此时有多少个 \(x\) 的低 \(k\) 位组合满足: 这低 \(k\) 位能且仅能与集合 \(S\subseteq[:2^m-1]\) 中的整数拼出一个存在奇数次的 \(x\)}. 我们对于当前 bit 可以出现在的位置集合 \(T\in\{0,1\}^m\), 预处理 \((S,T)\mapsto (R_0,R_1)\) 表示状态 \(S\) 经过可选集合为 \(T\) 的位转移到的新状态, 其中 \(R_0\) 表示第 \(k\) 位 (转移完成后被确定的位) 是 \(0\) 的状态, \(R_1\) 同理. 这样转移可以 \(\mathcal O(1)\) 完成, 最终复杂度 \(\mathcal O(m^22^{2m})-\mathcal O(w2^m)\), 其中 \(w=\log V=31\). 预处理也许可以用出色的位运算技巧再优化优化 (啊, 好像不如每次现场算转移哈).
10.「NOI Simu.」过山车 ⭐
- Private link & Submission.
- 「A.图论-网络流-费用流」
虽然鉴定为不如无限之环, 但不可否认这还是一个有点意思的网络流建图.
网格图上的简单环一定是二分的, 借此我们可以扔掉诡异的 "存在可行流" 限制, 转而在二染色后描述 "每个点都和两个异色点配对". 我们要求, 若一个点和它的两个配对点贡献, 则不贡献收益, 否则贡献 \(a_{i,j}\) 的收益. 换换等价表述, 若一个点在横向两个邻接点和纵向两个邻接点里分别选了一个, 才能贡献 \(a_{i,j}\) 的收益. "选得多" 优于 "选得少", 这样就可以描述了:
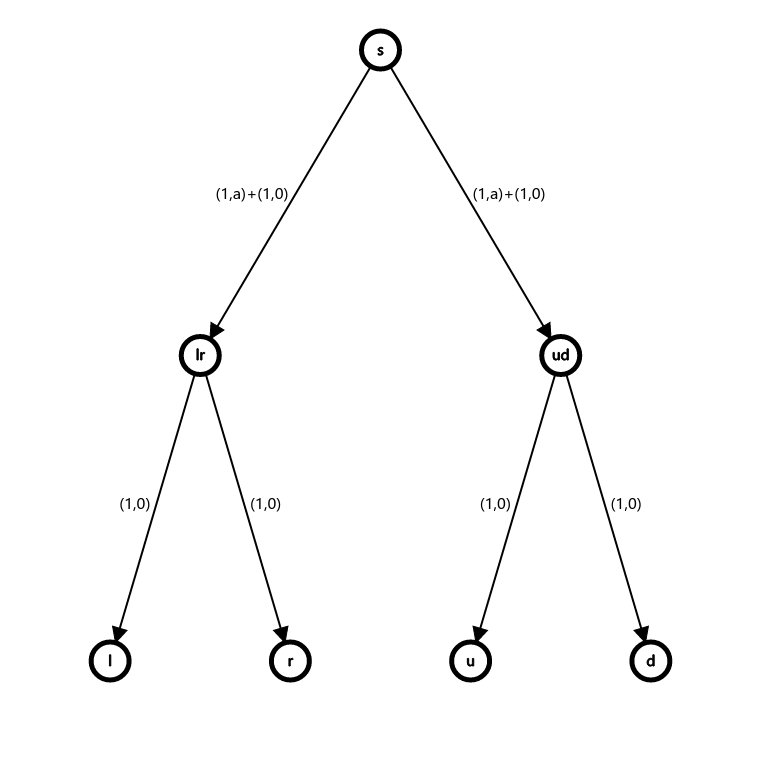
跑最大费用最大流, 若流量合法, 答案就是最大费用减去 \(\sum_ia_i\). 复杂度 \(\mathcal O(\text{Dinic}(5nm,9nm))\).
11.「NOI Simu.」木棍 ⭐
- Private link | 不想写 (星星眼.jpg
- 「A.图论-差分约束」
把木棍缩到左端点, 如果 \(m=0\) 且 \(k=1\), 这就是一个 Hall 定理的事儿. 据此我们也能发现, 把所有端点离散化, 仅考虑区间上 Hall 定理的判据, 仍然是等价的判定.
一维的规划问题, 想想差分约束? 设 \(s_i\) 表示 \(i\) 之前放置的木棍数量, 那么限制条件形如 \(s_r-s_{l-1}\ge x\). 的确可行. 当 \(k\neq1\) 时, 我们就有限制 \(s_{i+k}-s_i\le1\), \(m\neq0\) 时, 通过 \(s_{y_i}-s_{x_i-1}\le c_i\) 也能描述这些要求, 最后加上前缀和的固有条件 \(s_i\ge s_{i-1}\), 跑差分约束即可.
直接 SPFA 最坏 \(\mathcal O(n^3)\), 可以通过线段树维护整体转移做到 \(\mathcal O(n^2\log n)\).
12.「UR #11」「UOJ #169」元旦老人与数列 ⭐
- Link & Submission.
- 「A.数据结构-线段树」
Segment Tree Beats!k
嗯, 就用这玩意儿维护就行. 为了更方便维护历史最小值, 我们可以把所有修改标记变成 (当前增量, 前缀增量最小值) 这样的数对, 对区间的最小值和其他值需要分别维护不同的标记. \(\mathcal O(n\log^2 n)\).
13.「UR #12」「UOJ #180」实验室外的攻防战
- Link & Submission.
设 \(x\) 在 \(a\) 中出现的位置是 \(p_x\), 在 \(b\) 中出现的位置是 \(q_x\), 显然应当满足 \(\forall x<y,~p_x<p_y\Rightarrow q_x<q_y\), 有端 (指迅速搓了一发暴力) 猜测这是充要条件, 我们只需要实现快速检查. 若某对 \((x,y)\) 导致非法, 必然有点 \((p_x,q_x)\) 在点 \((p_y,q_y)\) 的左上方. 三维偏序走一走就行, 只需要检查偏序存在性, \(\mathcal O(n\log n)\).
14.「UR #13」「UOJ #186」Yist
- Link & Submission.
若存在可行的消除方案, 则必然存在一种被删除元素递增的删除方案. 假设某个询问串是 \(\{s_n\}\), 那么对于某个 \(s_i=0\), 它就需要能在序列 \(\{a_j\mid s_j=1\lor a_j\ge a_i\}\) 中被第一个删除, 也即存在一个以 \(a_i\) 为最小值的长度为 \(x\) 的子段.
可见, 我们只需要求出每个 \(a_i\) 对应的最长子段的最小长度就能得到答案. 按值从大到小考虑 \(s_i=0\) 的 \(a_i\), 将其加入到序列中暴力向左右扩展, 遇到已经被扩展过的结点直接跳过当前检查 (当前子段不短于曾经扩展这个位置的元素), 这样就 \(\mathcal O(nq)\) 了.
15.「UR #13」「UOJ #187」Ernd ⭐
- Link & Submission.
- 「A.DP-斜率优化」「B.离线」
令 \(f(i)\) 表示你觉得它该表示的东西, 那么 \(f(i)\) 有两类转移:
\[f(i)\overset{\max}{\gets} f(j)+1\quad(|a_i-a_j|\le b_i-b_j),\\ f(i)\overset{\max}{\gets}f(k)+(i-j+1)^2\quad(|a_j-a_k|\le b_j-b_k,[j,i]\text{ is combo-able}). \]形如 \(|a_i-a_j|\le b_i-b_j\) 的限制可以拆成 \(a_i-a_j\le b_i-b_j\land a_j-a_i\le b_i-b_j\), 它也描述了点 \((b_i-a_i,b_i+a_i)\) 和点 \((b_j-a_j,b_j+a_j)\) 的偏序关系, 所以前面一个转移可以根据 \(b_i-a_i\) 离线后用 BIT 维护 \(y\) 轴上的偏序贡献解决.
显然, 一列可 combo 的子段在上述离线过程中肯定会被依次取出来, 我们可以在 \(j\) 处转移时顺便将 \((j,\max\{f(k)\}+(j-1)^2)\) 放入 \(j\) 所在 combo 连续段的凸包上, 在 \(i\) 被拿出来的时候就弹一弹凸包进行第二类转移. 最终复杂度 \(\mathcal O(n\log n)\).
标签:Set,log,Submission,Solution,Link,UR,日点,UOJ,mathcal From: https://www.cnblogs.com/rainybunny/p/17475252.html